Намагничивание магнетика

Под действием внешнего магнитного поля магнитные моменты молекул приобретают преимущественную ориентацию, суммарный магнитный момент становится отличным от нуля , вещество намагничивается. Вещества, способные намагничиваться, получили название магнетиков. Термин этот возник исторически: когда-то считалось, что магнетики — это некоторый класс веществ. С современной же точки зрения все вещества без исключения — магнетики. Намагничивание магнетика характеризуется магнитным моментом единицы объема. Эту величину называют вектором намагничивания (или намагниченностью) :

,

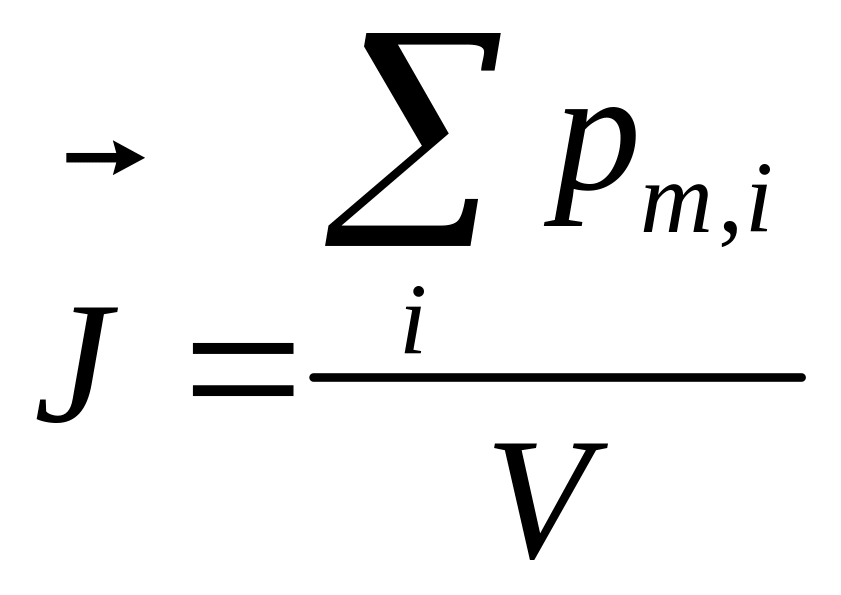где — магнитный момент отдельной молекулы, а суммирование ведется по всем молекулам объема . При неоднородном намагничивании вектор намагниченности в данной точке определится выражением

,

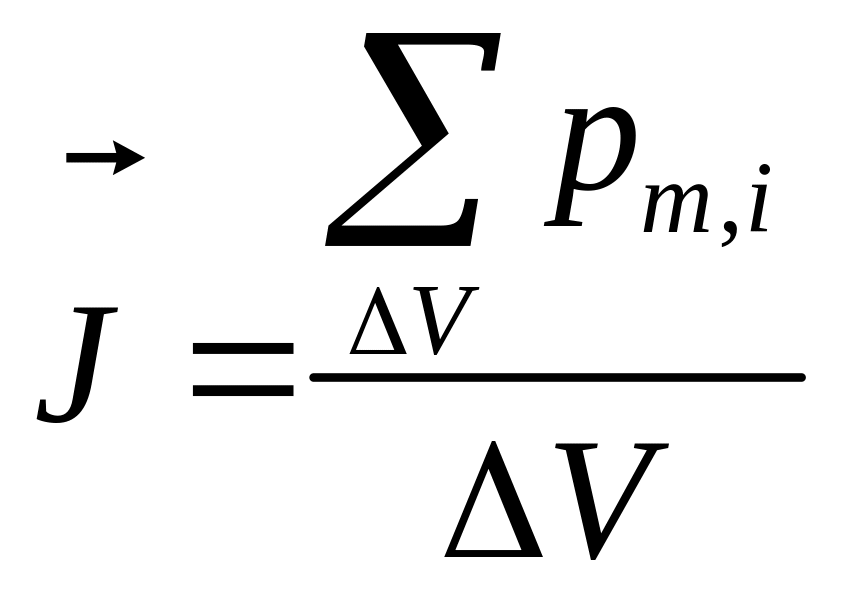где суммирование ведется по всем молекулам в физически малом объеме , в окрестности рассматриваемой точки. Размерность в системе СИ:

.

Магнитные поля молекулярных токов в намагниченном веществе уже не компенсируют друг друга, и возникает поле , обусловленное намагничиванием вещества. Это поле накладывается на внешнее намагничивающее поле , и в сумме дают результирующее поле

.

Напряженность магнитного поля. Теорема о циркуляции напряженности магнитного поля

Поскольку магнитное поле в веществе есть результат наложения полей макроскопических и молекулярных токов, то теорема о циркуляции индукции магнитного поля по замкнутому контуру записывается в следующем виде

,

где — сумма макроскопических токов, охватываемых контуром интегрирования, — сумма молекулярных токов, охватываемых контуром интегрирования.

Можно доказать, что циркуляция намагниченности вдоль замкнутого контура есть алгебраическая сумма молекулярных токов, охватываемых этим контуром:

,

тогда циркуляция индукции магнитного поля в веществе запишется как

.

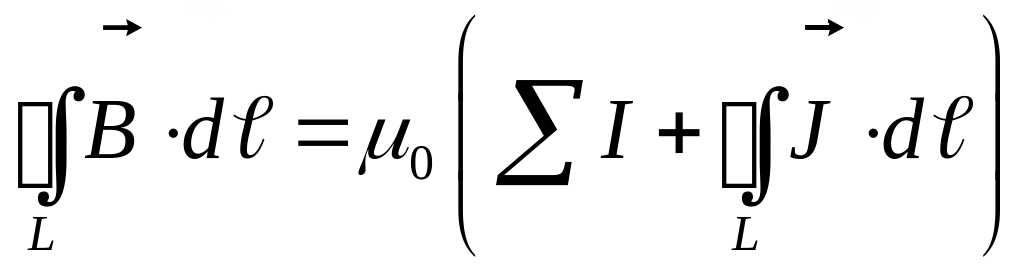Разделим обе части этого уравнения на и перенесем циркуляцию намагниченности в левую часть или

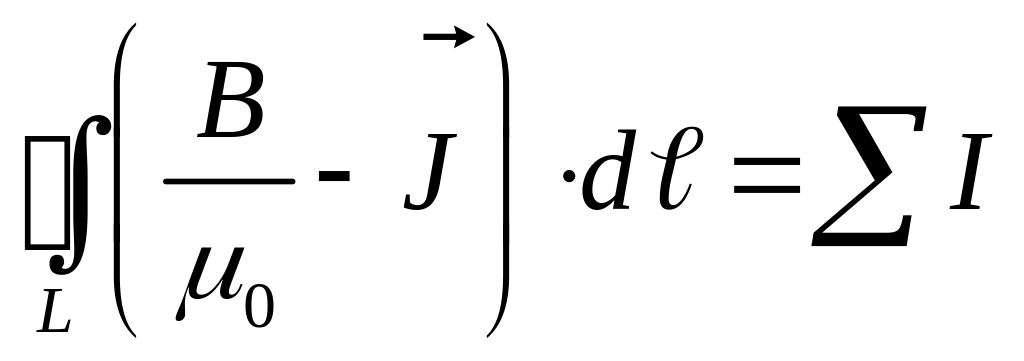
Введем вспомогательный вектор, называемый напряженностью магнитного поля , равный величине стоящей под интегралом в скобках

.

Циркуляция вектора по произвольному замкнутому контуру равна алгебраической сумме макроскопических токов проводимости, охватываемых этим контуром

.

Это выражение представляет собой теорему о циркуляции вектора . В дифференциальной форме эта теорема имеет вид

,

т. е. ротор вектора равен плотности тока проводимости в той же точке вещества.

Напряженность магнитного поля , как и намагниченность , измеряется в амперах на метр .

Магнитная проницаемость среды. Классификация магнетиков

Намагниченность принято связывать не с магнитной индукцией, а с напряженностью поля. В каждой точке магнетика

где — безразмерная величина называется магнитной восприимчивостью. Тогда , откуда . Безразмерная величина называется относительной магнитной проницаемостью вещества. С учетом этого

или .

В вакууме , , а индукция магнитного поля связана с напряженностью соотношением . В магнитной среде , откуда .

То есть относительная магнитная проницаемость среды показывает во сколько раз индукция магнитного поля в среде вследствие ее намагничивания больше индукции магнитного поля в вакууме.

В зависимости от знака и величины магнитной восприимчивости все магнетики подразделяются на группы:

1. диамагнетики, у которых величина отрицательна и мала по абсолютной величине ( 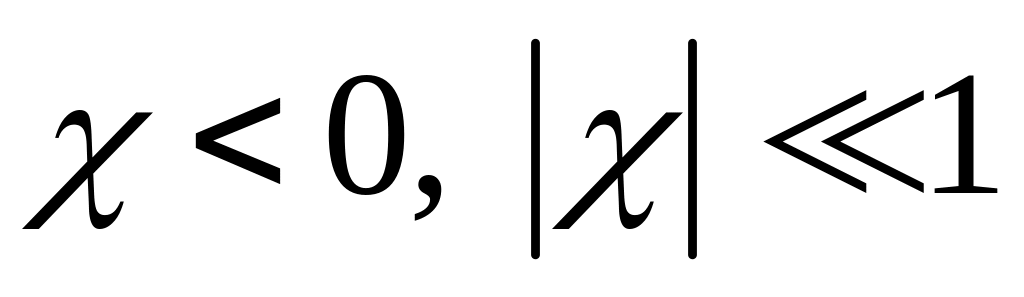), обычно ;

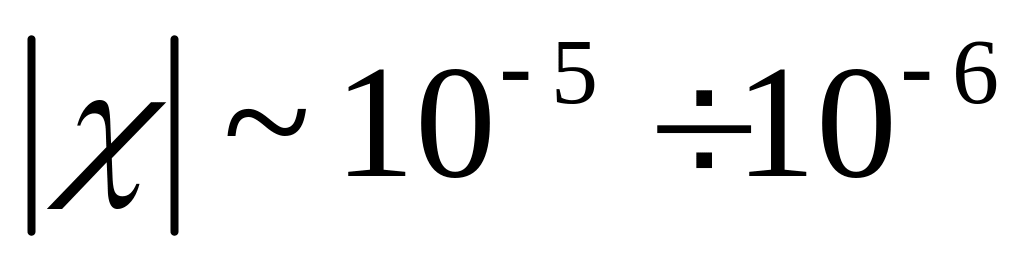2. парамагнетики, у которых величина положительна, но также мала по абсолютной величине ( 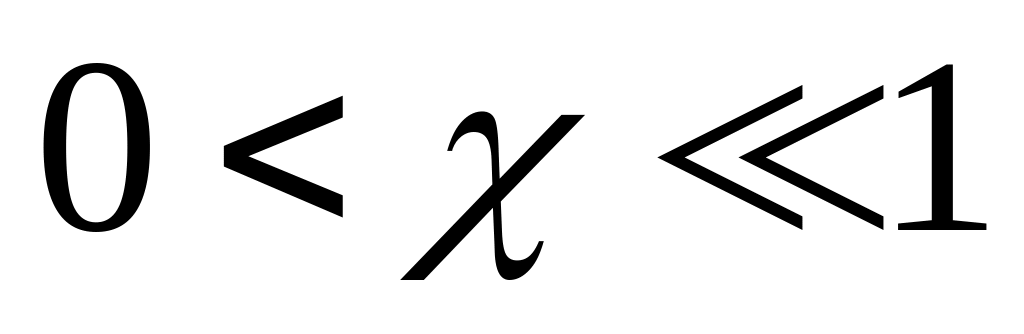), обычные значения ;

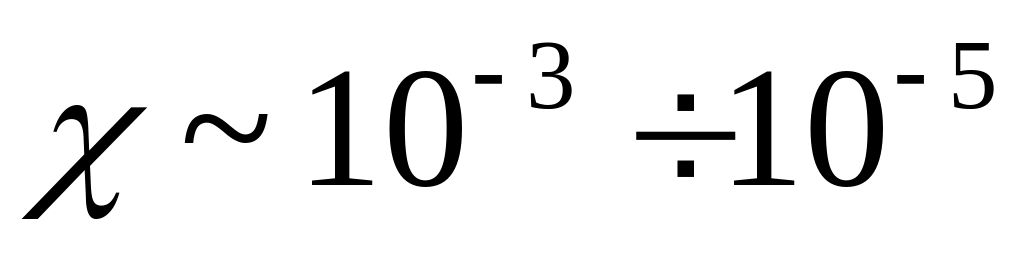3. ферромагнетики, у которых величина положительна и достигает больших значений до . Ферромагнетики относятся к классу магнитоупорядоченных веществ, т. е. магнетиков, у которых магнитные моменты упорядочены относительно друг друга даже в отсутствии внешнего магнитного поля. Из всего класса магнитоупорядоченных веществ рассмотрим только ферромагнетики.