
- •Магнитное поле
- •Сила Лоренца
- •Принцип действия циклических ускорителей заряженных частиц.
- •Эффект Холла.
- •Магнитное поле движущегося заряда
- •Сила Ампера
- •Закон Био —– Савара — Лапласа
- •Магнитное поле прямолинейного проводника с током
- •Магнитное поле кругового тока
- •Взаимодействие параллельных проводников с током. Единица силы тока.
- •Графическое представление поля . Теорема Гаусса
- •Циркуляция магнитного поля.
- •Ротор магнитного поля.
- •Применение теоремы о циркуляции вектора Магнитное поле соленоида
- •Магнитное поле тороида
- •Контур с током в магнитном поле. Магнитный момент контура с током.
- •Работа по перемещению проводника и контура с током в магнитном поле
- •Магнитное поле в веществе Элементарные носители магнетизма
- •Намагничивание магнетика
- •Напряженность магнитного поля. Теорема о циркуляции напряженности магнитного поля
- •Магнитная проницаемость среды. Классификация магнетиков
- •Диамагнетизм
- •Парамагнетизм
- •Ферромагнетизм
- •Явление электромагнитной индукции. Закон Фарадея
- •Токи Фуко
- •Индуктивность контура. Индуктивность соленоида
- •Явление самоиндукции. Эдс самоиндукции
- •Наблюдение самоиндукции
- •Ток при замыкании и размыкании цепи
- •Энергия магнитного поля. Плотность энергии магнитного поля.
- •Явление взаимной индукции
- •Ток смещения. Уравнения Максвелла
- •Электронная теория проводимости металлов (классическая теория Друде — Лоренца)
- •Закон Ома в электронной теории
- •Закон Джоуля — Ленца в электронной теории
- •Закон Видемана — Франца в электронной теории
- •Затруднения классической электронной теории металлов
- •Сверхпроводимость
Графическое представление поля . Теорема Гаусса
Как и другое векторное поле, поле может быть представлено с помощью линий вектора . Их проводят так, чтобы касательная к этим линиям в каждой точке совпадала с направлением вектора , а густота линий была бы пропорциональна модулю вектора в данном месте. Полученная таким образом геометрическая картина позволяет судить о конфигурации данного магнитного поля. А теперь сформулируем теорему Гаусса для магнитного поля: Поток вектора сквозь любую замкнутую поверхность равен нулю:
![]() .
.
Она выражает тот факт, что линии вектора не имеют ни начала, ни конца являются замкнутыми линиями. Поэтому число линий вектора , выходящих из любого объема, ограниченного замкнутой поверхностью , всегда равно числу линий, входящих в этот объем. Тогда и дивергенция векторного поля всюду будет равной нулю
 ,
или в другой записи
,
или в другой записи
![]() .
.
Это означает, что магнитное поле не имеет источников (магнитных зарядов). Магнитное поле порождают не магнитные заряды (которых в природе нет), а электрические токи. Этот закон является фундаментальным: он справедлив не только для постоянных, но и для переменных магнитных полей.
Циркуляция магнитного поля.
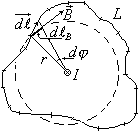
![]() ,
проведенного в магнитном поле, называется
линейный интеграл
,
проведенного в магнитном поле, называется
линейный интеграл
![]() ,
где
— вектор элементарной длины контура,
на которые мы разбиваем контур,
направленный вдоль обхода контура,
— индукция магнитного поля в точках
малого элемента контура. Проще всего
вычислить этот интеграл в случае прямого
тока, когда замкнутый контур лежит в
плоскости, перпендикулярной к току. На
рисунке ток перпендикулярен к плоскости
чертежа и направлен за чертеж. В каждой
точке контура вектор
направлен по касательной к окружности
(силовой линии), проходящей через эту
точку и составляет с током правовинтовую
систему. Скалярное произведение векторов
и
равно
,
где
— вектор элементарной длины контура,
на которые мы разбиваем контур,
направленный вдоль обхода контура,
— индукция магнитного поля в точках
малого элемента контура. Проще всего
вычислить этот интеграл в случае прямого
тока, когда замкнутый контур лежит в
плоскости, перпендикулярной к току. На
рисунке ток перпендикулярен к плоскости
чертежа и направлен за чертеж. В каждой
точке контура вектор
направлен по касательной к окружности
(силовой линии), проходящей через эту
точку и составляет с током правовинтовую
систему. Скалярное произведение векторов
и
равно
![]() ,
где
,
где
![]() — проекция вектора элемента контура
на направление поля
.
Эта проекция, как видно из рисунка равна
длине дуге окружности, являющейся
силовой линией магнитного поля
— проекция вектора элемента контура
на направление поля
.
Эта проекция, как видно из рисунка равна
длине дуге окружности, являющейся
силовой линией магнитного поля
![]() и принимает положительное значение,
если направление обхода контура
составляет с током правовинтовую систему
(направление проекции совпадает с
направлением поля
).
Здесь
и принимает положительное значение,
если направление обхода контура
составляет с током правовинтовую систему
(направление проекции совпадает с
направлением поля
).
Здесь
![]() есть угол, на который поворачивается
радиальная прямая при перемещении вдоль
контура на вектор
.
В этом случае циркуляция магнитного
поля
есть угол, на который поворачивается
радиальная прямая при перемещении вдоль
контура на вектор
.
В этом случае циркуляция магнитного
поля
![]() ,
и учитывая, что индукция магнитного
поля, созданного прямолинейным проводником
с током бесконечной длины
,
и учитывая, что индукция магнитного
поля, созданного прямолинейным проводником
с током бесконечной длины
![]() ,
мы получим
,
мы получим
![]() .
Интеграл
.
Интеграл
![]() ,
тогда
,
тогда
![]() .
.
Если сменить направление интегрирование контура на противоположное, по левовинтовой системе по отношению к току, то в этом случае проекции будут принимать отрицательные значения, и
![]() .
.
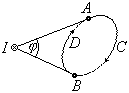
![]() и
и
![]() .
По участку
направление интегрирования составляет
с током правовинтовую систему, по участку
направление интегрирования составляет
с током левовинтовую систему. Тогда
.
По участку
направление интегрирования составляет
с током правовинтовую систему, по участку
направление интегрирования составляет
с током левовинтовую систему. Тогда
![]() .
.
Рассмотрим
циркуляцию магнитного поля, созданного
несколькими токами. По принципу
суперпозиции полей
![]() .
Тогда
.
Тогда
![]() ,
или
,
или
![]() .
.
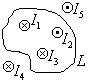
![]() .
.
Ток берется со знаком
«![]() »,
если он составляет с направлением
интегрирования правовинтовую систему,
и со знаком «
»,
если он составляет с направлением
интегрирования правовинтовую систему,
и со знаком «![]() »
при левовинтовой системе.
»
при левовинтовой системе.
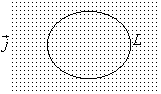
![]() заменяется через интеграл
заменяется через интеграл
![]() по поверхности S, натянутой на контур
интегрирования, а теорема о циркуляции
индукции магнитного поля принимает вид
по поверхности S, натянутой на контур
интегрирования, а теорема о циркуляции
индукции магнитного поля принимает вид
![]() .
.
