Сила Ампера
На
проводник с электрическим током в
магнитном поле, действует сила, называемая
силой Ампера. Сила Ампера
,
приложенная к малому элементу проводника
длины
,
с током силы I, создается
силами Лоренца, которые действуют на
движущие в проводнике носители тока.
Пусть
— объем элемента проводника, тогда
число носителей тока в нем
,
где
— концентрация носителей тока. Если
— средняя скорость упорядоченного
движения носителей тока, а
— заряд одного носителя, тогда сила
Ампера, действующая на элемент проводника,
будет равна
.
Учитывая, что
— плотность тока получим закон Ампера
.
Вектор
называют объемным элементом тока. Если
же ток течет по тонкому проводу, то он
называется линейным. Из-за малости
площади поперечного сечения проводника
можно считать, что плотность
тока постоянна,
,
и, следовательно,
.
Вектор
называют линейным элементом тока. Вектор
совпадает по направлению с вектором
плотности тока. Тогда закон Ампера для
линейного тока принимает вид
.
Сила
Ампера, действующая в магнитном поле
на проводник конечной длины с током
,
равна
.
В частности, если поле однородно, а проводник прямолинейный, то
.
Направление силы можно найти по правилу левой руки: если расположить ладонь левой руки так, чтобы вектор входил в ладонь, а четыре вытянутых пальца совпадали с направлением электрического тока в проводнике, то отставленный большой палец укажет направление силы Ампера. По модулю сила Ампера будет равна
,
где — угол между направлением тока (вектором плотности тока) в проводнике и вектором .
Из закона Ампера следует, что сила максимальна, если проводник с током расположен перпендикулярно к магнитному полю, тогда модуль вектора индукции :
.
Магнитная индукция
численно равна отношению максимальной
силы, действующей со стороны магнитного
поля на малый элемент проводника с
током, к произведению силы тока на длину
этого элемента. Направлен вектор
так, что
,
,
и
образуют правовинтовую тройку.
Закон Био —– Савара — Лапласа
Рассмотрим вопрос о нахождении магнитного
поля, создаваемого постоянными
электрическими токами. Этот вопрос
будем решать, исходя из закона
,
определяющего индукцию магнитного поля
равномерно движущегося точечного
заряда. Представив заряд
,
как заряд элементарного объема
токопроводящей среды
,
где
— объемная плотность заряда носителей
тока, и учитывая, что плотность тока
,
где
скорость упорядоченного движения
носителей тока, мы получим формулу
, (1)
выражающую индукцию
магнитного поля, созданного элементом
тока
.
Если же ток течет по тонкому проводу,
то
и для линейного элемента тока выражение
(1) принимает вид
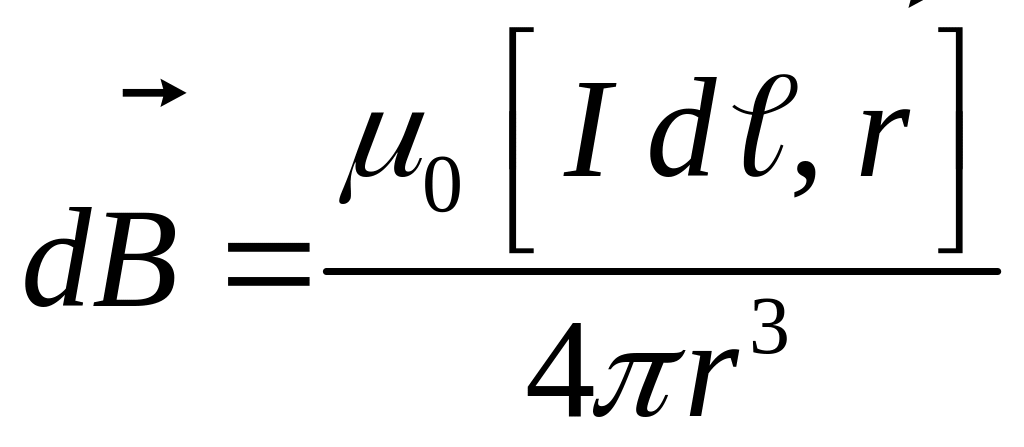. (2)
Направление вектора определяется правилом векторного произведения — правила буравчика. Острие буравчика направляют вдоль вектора (вдоль проводника в направлении тока), рукоятку вдоль радиус-вектора , проведенного от элемента тока к исследуемой точке поля, тогда направление движения конца рукоятки при правовинтовом вращении укажет направление вектора . Модуль вектора будет равен
,
где — угол между векторами и , r — модуль радиус-вектора .
Формулы (1) и (2) выражают закон Био — Савара — Лапласа. Био и Савар сформулировали закон для силы, с которой элемент тока действует на магнитный полюс. Лаплас проанализировал экспериментальные данные, полученные Био и Саваром, и нашел, что магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементами тока, на которые мысленно разбивают проводник с током. То есть полное поле , создаваемое всем проводником с током, в соответствии с принципом суперпозиции определяется в результате интегрирования выражений (1) или (2) по всем элементам тока:
,
.
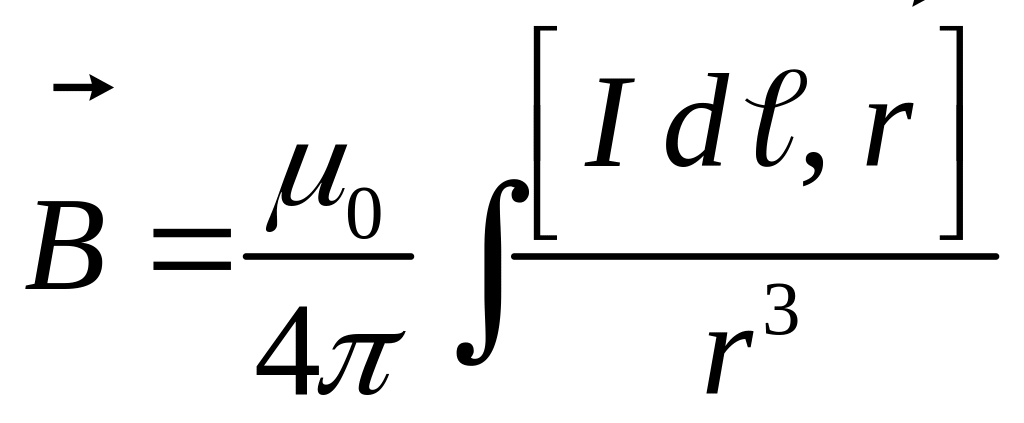Приведем несколько простейших примеров на нахождение индукции магнитного поля.