
- •Магнитное поле
- •Сила Лоренца
- •Принцип действия циклических ускорителей заряженных частиц.
- •Эффект Холла.
- •Магнитное поле движущегося заряда
- •Сила Ампера
- •Закон Био —– Савара — Лапласа
- •Магнитное поле прямолинейного проводника с током
- •Магнитное поле кругового тока
- •Взаимодействие параллельных проводников с током. Единица силы тока.
- •Графическое представление поля . Теорема Гаусса
- •Циркуляция магнитного поля.
- •Ротор магнитного поля.
- •Применение теоремы о циркуляции вектора Магнитное поле соленоида
- •Магнитное поле тороида
- •Контур с током в магнитном поле. Магнитный момент контура с током.
- •Работа по перемещению проводника и контура с током в магнитном поле
- •Магнитное поле в веществе Элементарные носители магнетизма
- •Намагничивание магнетика
- •Напряженность магнитного поля. Теорема о циркуляции напряженности магнитного поля
- •Магнитная проницаемость среды. Классификация магнетиков
- •Диамагнетизм
- •Парамагнетизм
- •Ферромагнетизм
- •Явление электромагнитной индукции. Закон Фарадея
- •Токи Фуко
- •Индуктивность контура. Индуктивность соленоида
- •Явление самоиндукции. Эдс самоиндукции
- •Наблюдение самоиндукции
- •Ток при замыкании и размыкании цепи
- •Энергия магнитного поля. Плотность энергии магнитного поля.
- •Явление взаимной индукции
- •Ток смещения. Уравнения Максвелла
- •Электронная теория проводимости металлов (классическая теория Друде — Лоренца)
- •Закон Ома в электронной теории
- •Закон Джоуля — Ленца в электронной теории
- •Закон Видемана — Франца в электронной теории
- •Затруднения классической электронной теории металлов
- •Сверхпроводимость
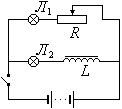
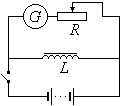
Наблюдение самоиндукции
Ток при замыкании и размыкании цепи
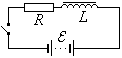
![]() ,
катушки с индуктивностью
и резистора с сопротивлением
.
После подключения источника ЭДС, до тех
пор, пока сила тока не достигнет
установленного значения
,
катушки с индуктивностью
и резистора с сопротивлением
.
После подключения источника ЭДС, до тех
пор, пока сила тока не достигнет
установленного значения
![]() ,
в цепи кроме ЭДС
будет действовать ЭДС самоиндукции
.
Следовательно, в соответствии с вторым
правилом Кирхгофа
,
в цепи кроме ЭДС
будет действовать ЭДС самоиндукции
.
Следовательно, в соответствии с вторым
правилом Кирхгофа
![]() ,.
,.
Решим полученное
дифференциальное уравнение. Перенесем
в левую часть и части поменяем местами,
изменив знаки на противоположные
![]() ,
или
,
или
![]() ,
,
![]() .
Разделим переменные, для этого умножим
обе части уравнения на
.
Разделим переменные, для этого умножим
обе части уравнения на
![]() и разделим на
и разделим на
![]() .
Тогда
.
Тогда
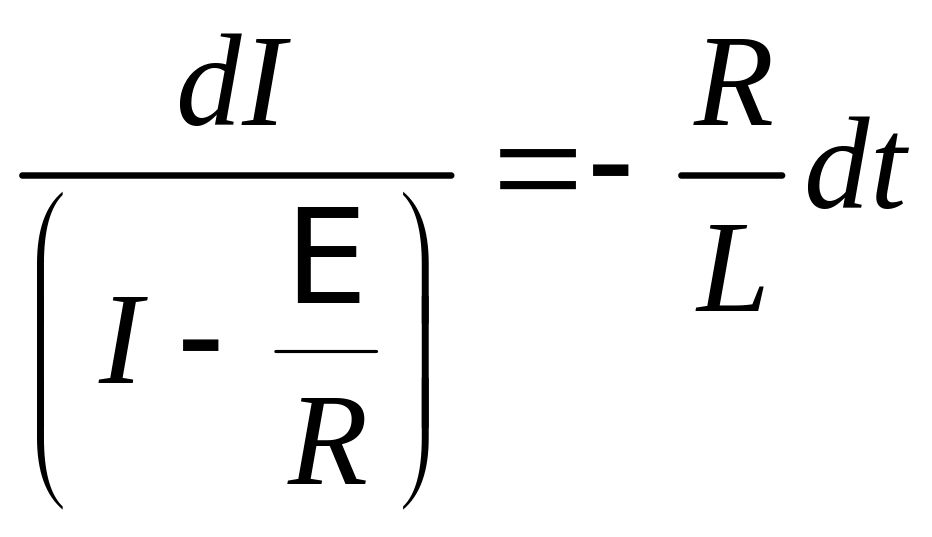 .
.
После
интегрирования получим
![]() ,
а после потенцирования
,
а после потенцирования
![]() ,
или
,
или
![]() .
Постоянную интегрирования
найдем по начальных условий. Если
.
Постоянную интегрирования
найдем по начальных условий. Если
![]() ,
то
,
то
![]() ,
тогда
,
тогда
![]() ,
следовательно,
,
следовательно,
![]() ,
или
,
или
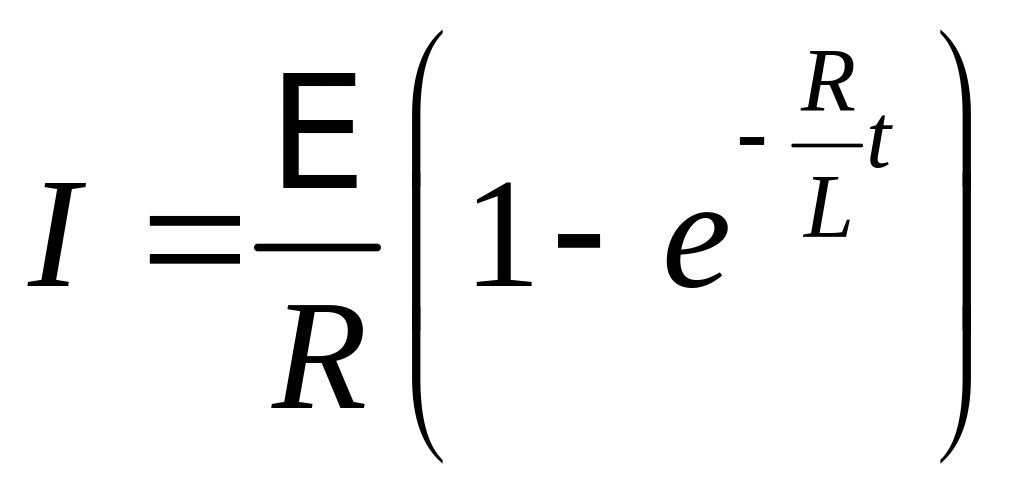 .
.
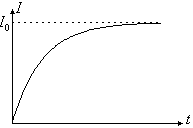
![]() — установившееся значение тока, запишем
— установившееся значение тока, запишем
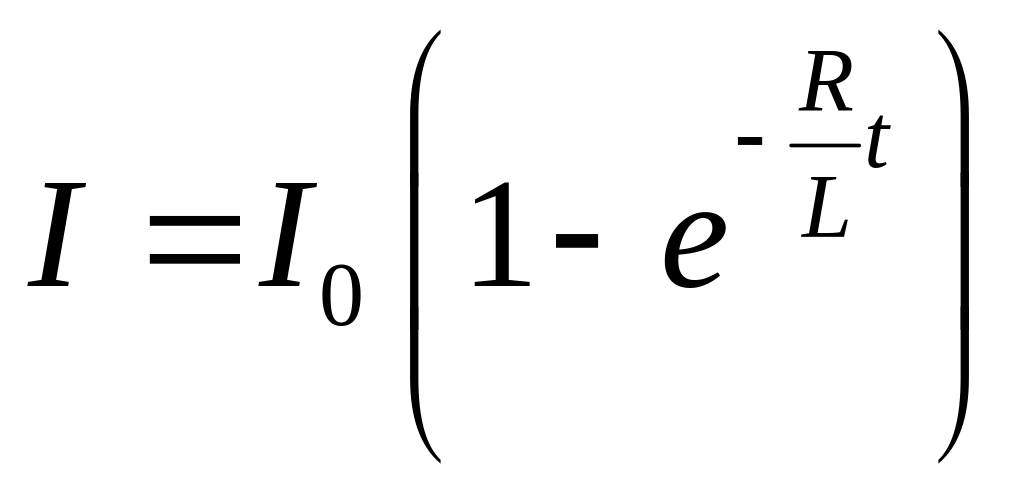 .
.
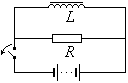
Эта функция описывает нарастание тока в цепи после подключения к ней источника ЭДС. График функции дан на рисунке.
![]() ,
и этот ток создает магнитное поле. При
размыкании ключа остается последовательная
цепь из катушки и резистора. Как только
сила тока в цепи начнет убывать, возникает
ЭДС самоиндукции, противодействующая
этому убыванию. Следовательно, в
соответствии с законом Ома
,
и этот ток создает магнитное поле. При
размыкании ключа остается последовательная
цепь из катушки и резистора. Как только
сила тока в цепи начнет убывать, возникает
ЭДС самоиндукции, противодействующая
этому убыванию. Следовательно, в
соответствии с законом Ома
![]() ,
или
,
или
![]() .
Это уравнение представляет собой
линейное однородное дифференциальное
уравнение первого порядка. Разделив
переменные, получим
.
Это уравнение представляет собой
линейное однородное дифференциальное
уравнение первого порядка. Разделив
переменные, получим
![]() .
.
Отсюда после
интегрирования
![]() .
Потенцирование этого соотношения дает
.
Потенцирование этого соотношения дает
![]() .
.
Значение
постоянной интегрирования
найдем из начальных условий. При
сила тока имела значение
![]() .
Тогда
.
Тогда
![]() ,
т. е.
,
т. е.
![]() .
Следовательно,
.
Следовательно,
![]() .
.
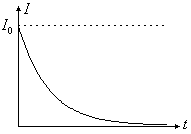
Итак, после отключения источника ЭДС сила тока в цепи не обращается мгновенно в нуль, а убывает по экспоненциальному закону. График убывания дан на рисунке.
