3. Расчет плиты по предельным состояниям первой группы

Расчет по прочности железобетонных элементов должен производиться для сечений, нормальных к их продольной оси, а также для наклонных к ней сечений наиболее опасного направления. При наличии крутящих моментов следует проверить прочность пространственных сечений, ограниченных в растянутой зоне спиральной трещиной наиболее опасного из возможных направлений. Кроме того, следуют производить расчет элементов на местное действие нагрузки (смятие, продавливание, отрыв).

3.1 Расчет прочности плиты по сечению, нормальному к продольной оси:

Μ=86,45 кН· м

Сечение тавровое с полкой в сжатой зоне (рис.1). Согласно [1] при

h′_f ∕ h=31∕220=0,14≥0,1 расчетная ширина b′_f=2160мм (2,16м)

Параметр а=30мм, рабочая высота h₀= h-а=220-30=190мм

Проверяем условие:

R_b· b′_f · h′_f · (h₀-0,5 h′_f )≥М

17,55· 2160 ·31 · (190-0,5· 31)=205· 10⁶ Н· мм=205кНм М=86,45кНм

Т.е. граница сжатой зоны проходят в полке и расчет производим как для прямоугольного сечения шириной b=b′_f=2160мм.

Определяем значение:

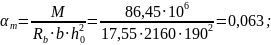
Пользуясь СНиП 2.03.01.-84* находим:

ξ=0,063 и ζ=0,967.

Вычислим относительную граничную высоту сжатой зоны ξ_R по формулам [1, n.3.12] :

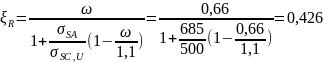
где ω – характеристика сжатой зоны бетона;

ω =α-0,008· R_b=0,8-0,008·17,55=0,066;

где α=0,8 для легкого бетона;

α=0,85 для тяжелого бетона;

G_SR-напряжение в арматуре:

σ_SR=R_S+400-σ_SP=915+400-630=685МПа

(предварительное напряжение принято с учетом полных потерь σ_SP=0,7·900=630МПа); σ_SС,U=500МПа при γ_b2 1,0.

Если соблюдается условие  < _R, расчетное сопротивление арматуры R_s в оговоренных случаях умножается на коэффициент условий работы _s6, определяемый по формуле

_s6 =   (  1)   ,

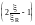
где  - коэффициент, принимаемый равным для арматуры классов:

A-IV............................................................ 1,20

A-V, В-II, Вр-II, К-7 и К-19 ...................... 1,15

A-VI ........................................................... 1,10

прочих ....................................................... 1,00

Если  < 0,5_R, можно, не пользуясь формулой, принимать _s6 = .

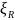Так как ξ=0,063 0,5 =0,5·0,426=0,213, то согласно [3, п.3,7], коэффициент условий работы, учитывающий сопротивление напрягаемой арматуры выше условного предела текучести можно принимать равным _s6 = =1,15.

Вычислим требуемую площадь сечения растянутой напрягаемой арматуры:

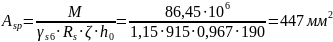
Принимаем 12 стержней диаметром 7, Вр-II, А_SР= 462мм²

3.2 Проверка прочности плиты по наклонным сечениям к продольной оси:

Q_max=58,86кН; q₁= q=20,04кН/м

Поскольку [2, п.5,26] допускается не устанавливать поперечную арматуру в многопустотных плитах, выполним проверку прочности сечения плиты на действие поперечной силы при отсутствии поперечной арматуры согласно [2, п.3,32].

Проверим условие [3]:

2,5 ·Rbt ·b · h0 Qmax;

где b=2160-11·159=441мм

2,5·1,17·441·190=228,4·10³Н=228,4 кН ≥58,86кН

Условие выполняется.

Проверим условие [3], принимая упрощение Q_b1 = Q_b,min и

С=2,5· h₀=2,5· 0,19=0,475м

Находим усилие обжатия от растянутой продольной арматуры

Р=0,7· σ_SP · А_SР = 0,7· 1000 · 462=323,4·10³ Н=323,4 кН.

Вычислим:

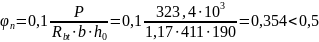
Согласно [1] φ_b3=0,4, тогда:

Q_b,min= φ_b3 · (1+ φ_n) ·R_bt ·b · h₀ = 0,4 · (1+ 0,354) ·1,17 ·411· 190=

=49,5·10³Н=49,5кН

Q_b1 = Q_b,min=49,5кН

Так как

Q = Q_max - q₁·c= 58,86 – 20,04 · 0,475=49,3кН

Q≤ Q _b1

Следовательно, для прочности наклонных сечений по расчету арматуры не требуется.