Лабораторная работа № 7 экспериментальное исследование нормальных контактных напряжений при осадке

1 Цель работы

Изучить методику и приобрести практические навыки экспериментального определения контактних напряжений. Экспериментально изучить влияние трения на форму эпюры контактних напряжений при осадке и на величину усилия осадки.

Вследствие большого объема и высокой значимости работа выполняется на двух занятиях. На первом занятии нормальные контактные напряжения определяются при осадке свинцового образца со смазкой. На втором занятии контактные напряжения определяются при осадке образца без смазки.

2. Теоретические сведения

Анализ операции осадки низкой цилиндрической заготовки является классическим примером применения инженерного метода теории пластической деформации для решения технологических задач. Суть инженерного метода состоит в совместном решении приближенного уравнения равновесия, условия пластичности и уравнения, описывающего закон трения (Э. Зибеля или О. Кулона). В результате анализа определяется распределение контактных напряжений и выводится формула для расчета усилия необходимого для осадки. Рассмотрим основные этапы этого анализа.

Так как форма заготовки и ее нагружение при осадке цилиндрической заготовки являются осесимметричными, то анализ целесообразно проводить в цилиндрической системе координат --z. Рассмотрим уравнение равновесия внутренних сил, действующих в направлении .

. (1)

Предположим, что выполняется условие полной пластичности _=_. В этом случае уравнение равновесия (1) принимает вид

. (2)

Предположим, что касательные напряжения _z изменяются по высоте цилиндрической заготовки по линейному закону, что можно выразить формулой

, (3)

где _k – напряжение трения на поверхности контакта заготовки и осадочных плит и H – половина высоты заготовки. Предположим, что трение на контактной поверхности описывается законом Э. Зибеля

, (4)

где m – фактор трения и _S – напряжение текучести материала заготовки. Подставив выражение (4) в формулу (3), получаем

. (5)

Предположим, что напряжение _ не зависит от координаты z, является оправданным для низких заготовок. В этом случае частную производную в уравнении (2) можно заменить полной, т.е.

. (6)

Подставляя выражения (5) и (6) в формулу (2), получаем приближенное уравнение равновесия

. (7)

Предположим, что материал заготовки является идеально пластическим, т.е. _= const. Тогда после разделения переменных в (7) и интегрирования, приходим к выражению

, (8)

где C – постоянная интегрирования, которая находится из условия, что при =D/2 напряжение _=0.

. (9)

Подставляя (9) в формулу (8), находим зависимость, описывающую изменение напряжения _ вдоль координаты 

. (10)

Для нахождения аналогичного распределения для напряжения _z воспользуемся условием пластичности Теска

, (11)

где _max и _min – максимальное и минимальное главные напряжения, соответственно. Предположим, что напряжения _ и _z (очевидно, что _ > _z) близки к главным напряжениям _max и _min. Тогда условие пластичности Теска можно приближенно представить как

. (12)

В результате совместного рассмотрения зависимостей (10) и (12) получается выражение (13), описывающее распределение напряжения _z по координате . Из выражения (13) следует, что рассматриваемое распределение является линейным.

. (13)

На рис.1 показана в общем виде эпюра напряжений _z соответствующая формуле (13).

_s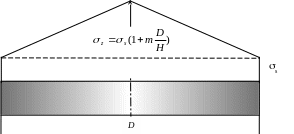

Рисунок 1 – Распределение напряжений _z вдоль координаты .

Усилие, необходимое для осадки цилиндрической заготовки – P, можно вычислить по формуле

, (14)

где S – площадь контактной поверхности. Из формулы (14) следует, что усилие осадки можно определить как объем эпюры напряжений _z. Из рис. 1 следует, что эту эпюру можно представить состоящей из цилиндра и конуса диаметром D и высотой _s и _smD/H ,соответственно. Суммарный объем этих частей эпюры выражается формулой

. (15)

Из (15) получается формула для определения усилия осадки, которая называется формулой Э. Зибеля

. (16)

Формула Э.Зибеля имеет структуру характерную для формул, полученных инженерным методом теории пластической деформации. Первый сомножитель в её правой части описывает влияние на усилие осадки свойств материала. Второй сомножитель описывает влияние трения. Третий сомножитель описывает влияние размеров заготовки.

В лабораторной работе для экспериментальной проверки влияния трения на вид эпюры контактных напряжений и на усилие осадки используется метод отпечатков и специальное приспособление, показанное на рис. 2. При осадке со стороны деформируемого образца 6 на штифт 3 и через него на шарик 4 передается некоторое усилие. Величину этого усилия и можно определить по диаметру отпечатка, который оставляет шарик на пластине 5. Разделив усилие на площадь сечения штифта можно определить контактное напряжение.

Зависимость контактного напряжения от диаметра отпечатка получают в специальных тарировочных опытах, когда штифт нагружается известным усилием и затем измеряется диаметр отпечатка и рассчитывается контактное напряжение. Результаты тарировочных экспериментов приведены в Таблице 1.

Таблица 1 – Зависимость нормального контактного напряжения на штифте от диаметра отпечатка шарика

d, мм	1,25	1,63	2,35	2,59
σk, MПа	12,7	25,5	50,9	76,4

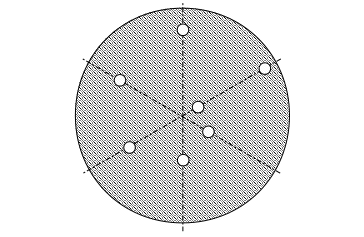
Рисунок 2 – Приспособление для определения контактных напряжений при осадке свинцовых дисков:

1 – верхняя плита; 2 – нижняя плита; 3 – штифт; 4 – шарик; 5 – пластина; 6 – образец