8.3. Магнитное поле медленно движущегося точечного заряда

Опыт показывает, что элементарное магнитное поле, созданное зарядом q, который движется со скоростью v медленно (v<< c) в точке, характеризуемой радиус-вектором r описывается формулой:

(6)

Здесь, как обычно, - радиус-вектор, начинающийся на точечном заряде q и заканчивающийся в точке наблюдения магнитного поля .

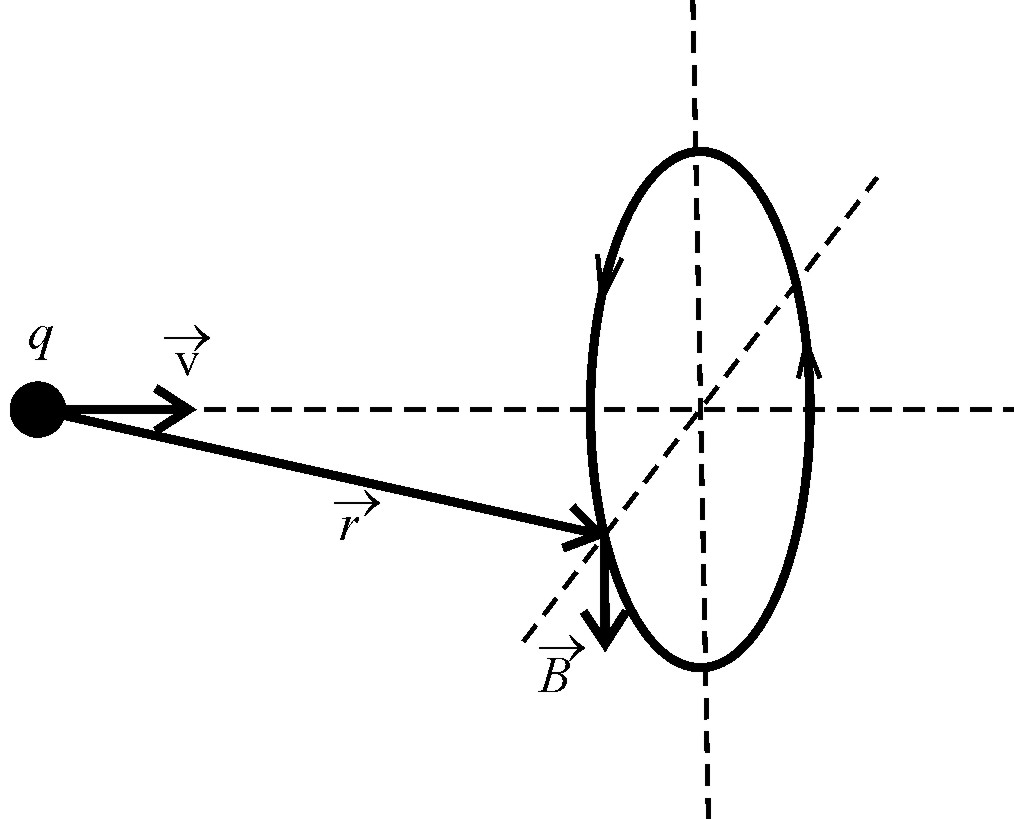
Рис. Взаимное расположение вектора скорости точечного заряда q, вектора магнитного поля , созданного этим движущимся зарядом, и радиус-вектора точки наблюдения. Окружность изображает одну из линий магнитного поля

Согласно (6) вектор направлен перпендикулярно плоскости, в которой расположены векторы и , причем линии поля индукции представляют собой окружности (Рис.). При использовании формулы (6) важно понимать, что все три вектора ( ,  и ), входящие в нее, соответствуют одному и тому же моменту времени.

Замечание. Довольно часто для сокращения записей вводят величину (“мю ноль”), определяя ее как (Согласно решению XVII Генеральной конференции по мерам и весам значение установлено как не подлежащее уточнению)

Величину ₀ обычно называют магнитной постоянной. Никакого физического смысла (как и электрическая постоянная ₀) она не имеет.

8. 4. Два частных случая преобразования полей и .

В настоящем параграфе, опираясь на специальную теорию относительности, рассмотрим два частных, но очень важных типа электромагнитного поля. В итоге обнаружим связь компонент и в электромагнитном поле каждого из двух типов.

1 случай. Если в некоторой системе отсчета электромагнитное поле является электрическим (т.е. ), то в другой системе отсчета , движущейся относительно К со скоростью , компоненты электромагнитного поля отличны от нуля и связаны соотношением:

Рассмотрим точечный заряд Q > 0, покоящийся в - системе отсчета. В точке на конце вектора электрическое поле описывается формулой:

. В системе отсчета , движущейся со скоростью , заряд Q движется со скоростью и создает на конце вектора (поперечные размеры не изменяются, только продольные) магнитное поле определяется по формуле (6):

,(7), где

поэтому

и электрическое поле:

(т.к. ).

Таким образом,

Таким образом, приходим к следующему выводу: если в некоторой системе отсчета электромагнитное поле является электрическим (  ), то в любой другой системе отсчета, движущейся относительно первой со скоростью , компоненты электромагнитного поля отличны от нуля и связаны друг с другом соотношением (7).

Отсюда, в частности, следует, что если в некоторой системе отсчета электрически заряженное тело имеет скорость , то электрическая и магнитная компоненты электромагнитного поля, создаваемого его зарядом, связаны в этой системе отсчета соотношением

(8)

2случай. Теперь рассмотрим другой тип электромагнитного поля, которое в K-системе отсчета имеет только магнитную компоненту: .

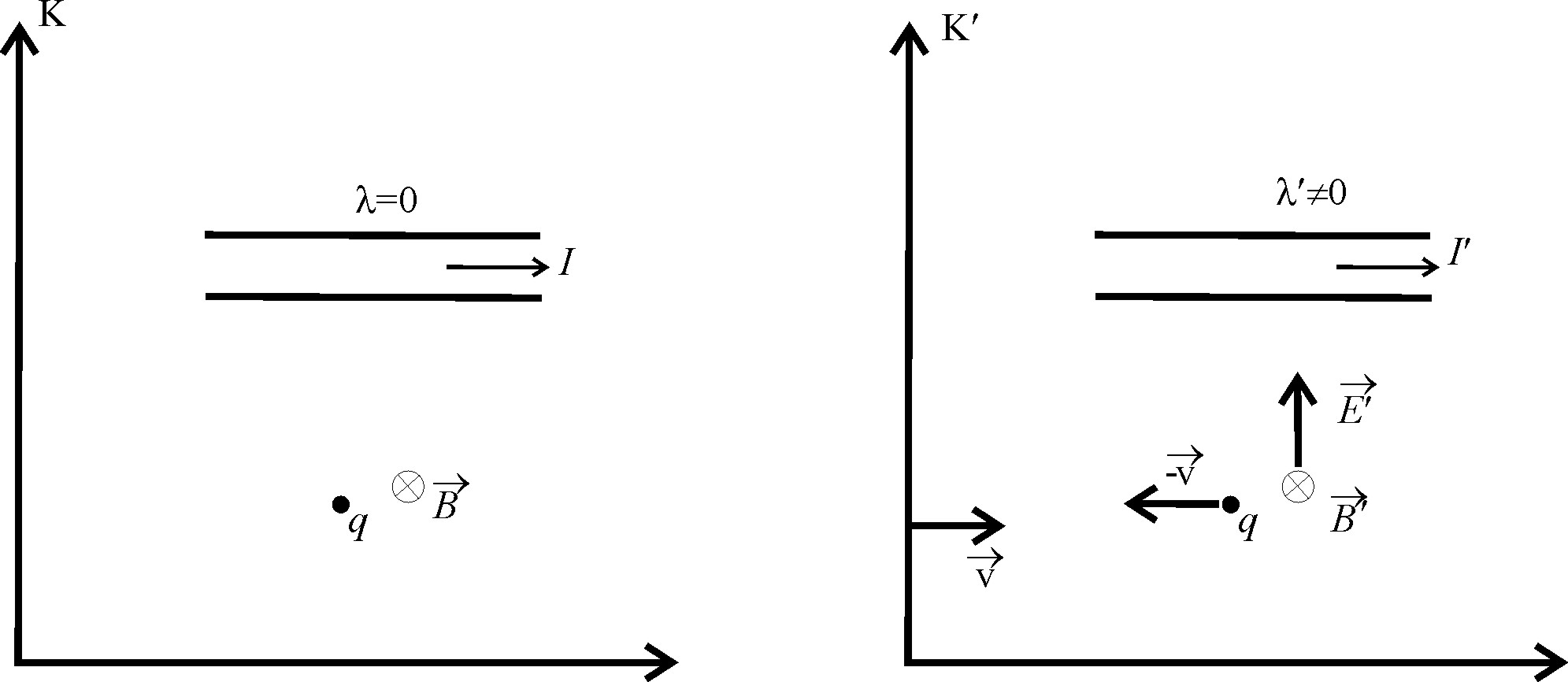
а) б)

Рис. а)Электронейтральный прямолинейный провод с током I и пробный заряд q покоятся в K-системе отсчета; б) проводник, но уже заряженный и с током наблюдается из -системы отсчета. Пробный заряд движется и испытывает действие как электрического, так и магнитного полей.

Такое поле в некоторой K-системе отсчета создает, например, электронейтральный (в этой системе отсчета) прямолинейный проводник с током I (Рис.а). На покоящийся в этой системе отсчета пробный заряд q не действует сила Лоренца, так как электрического поля нет, а магнитное на покоящийся заряд не действует. В другой системе отсчета , движущейся относительно системы S со скоростью вдоль тока I, проводник оказывается заряженным и создает поля (Рис.б). Пробный заряд q в системе отсчета движется со скоростью и потому испытывает действие как поля , так и поля :

Из релятивистской механики известно, что хотя сила не является величиной инвариантной по отношению к преобразованиям Лоренца, однако, если сила равна 0 в одной системе отсчета, то она отсутствует и во всех других инерциальных системах отсчета. Таким образом, поскольку, .Следовательно,

  (9)

Итак, если в некоторой системе отсчета электромагнитное поле является магнитным ( ), то в любой другой системе отсчета, движущейся со скоростью относительно первой, компоненты и электромагнитного поля отличны от нуля и связаны друг с другом соотношением (9).