8.1. Релятивистская природа магнитного поля.

Взаимодействие точечных неподвижных зарядов полностью описывается законом Кулона. Однако закон Кулона недостаточен для анализа взаимодействия движущихся зарядов, причем такой вывод следует не из конкретных особенностей кулоновского взаимодействия, а обусловливается релятивистскими свойствами пространства и времени и релятивистским уравнением движения. Это утверждение в принципе вытекает из таких соображений. Релятивистское уравнение движения

dp/dt = F (1)

Инвариантно и имеет одинаковый вид во всех инерциальных системах координат, в частности в системе координат к', которая движется равномерно и прямолинейно относительно к:

dp'/dt' = F' (2)

Буквы со штрихами обозначают величины, относящиеся к К'. В левые части этих уравнений входят чисто механические величины, поведение которых при переходе из одной системы координат в другую известно. Следовательно, можно связать между собой некоторой формулой левые части уравнений (8.1) и (8.2). Но тогда оказываются связанными между собой стоящие в правой части этих уравнений силы. Наличие такой связи обусловливается требованием релятивистской инвариантности уравнения движения. Поскольку в левые части уравнений (8.1) и (8.2) входят скорости, заключаем, что сила взаимодействия движущихся зарядов зависит от скорости и не сводится к кулоновской силе. Тем самым доказывается, что взаимодействие движущихся зарядов осуществляется не только кулоновской силой, но также силой другой природы, называемой магнитной.

( Пояснения к п 8.1. Для дополнительного изучения.

Релятивистское преобразование поперечной силы.)

Рисунок 1: две материальные точки с зарядами и удалены на расстояние друг от друга в лабораторной системе отсчета .

Взаимодействие – электростатическое (кулоновское отталкивание, т.к. заряды положительны).

Из закона Кулона

Рисунок 2. Инерциальная система отсчета движется вдоль оси со скоростью . В этой инерциальной системе отсчета заряды движутся со скоростями параллельно друг другу (два параллельных тока).

Механика Эйнштейна (специальная теория относительности) утверждает, что (*).

Выведем (*).

По определению импульса , , так как поперечная длина не преобразуется, то

, . Но нас интересует сила.

Известные нам преобразования Лоренца . Дифференцируем:

Таким образом, в отличие от механики Ньютона, в теории относительности поперечная сила зависит от скорости системы отсчета, и это позволяет объяснить происхождение магнитных сил.

8.2. Сила Лоренца и ее магнитная составляющая. Магнитное поле

В разделе “Электростатика” изучались свойства поля электрических сил , действующих на покоящийся пробный заряд q. В качестве характеристики поля был введен вектор   , не зависящий от величины пробного заряда q. Однако, как показывает опыт, сила , действующая на движущийся заряд, может отличаться от электрической силы . Это отличие связано с существованием так называемой магнитной силы .

Обобщением опытных данных являются следующие три основные свойства магнитной силы, действующей на движущуюся заряженную частицу.

1. Величина магнитной силы пропорциональна заряду движущейся частицы и величине ее скорости.

2. Направление магнитной силы всегда перпендикулярно направлению движения заряженной частицы.

3. В любой точке пространства существует такое направление, двигаясь в котором частица не испытывает действия магнитной силы. Другими словами существует такая ориентация вектора скорости, при котором магнитная сила равна нулю.

Перечисленные свойства магнитной силы можно описать количественно, для чего удобно ввести понятие магнитного поля.

Характеризуя это поле вектором индукции магнитного поля , запишем выражение для магнитной силы:

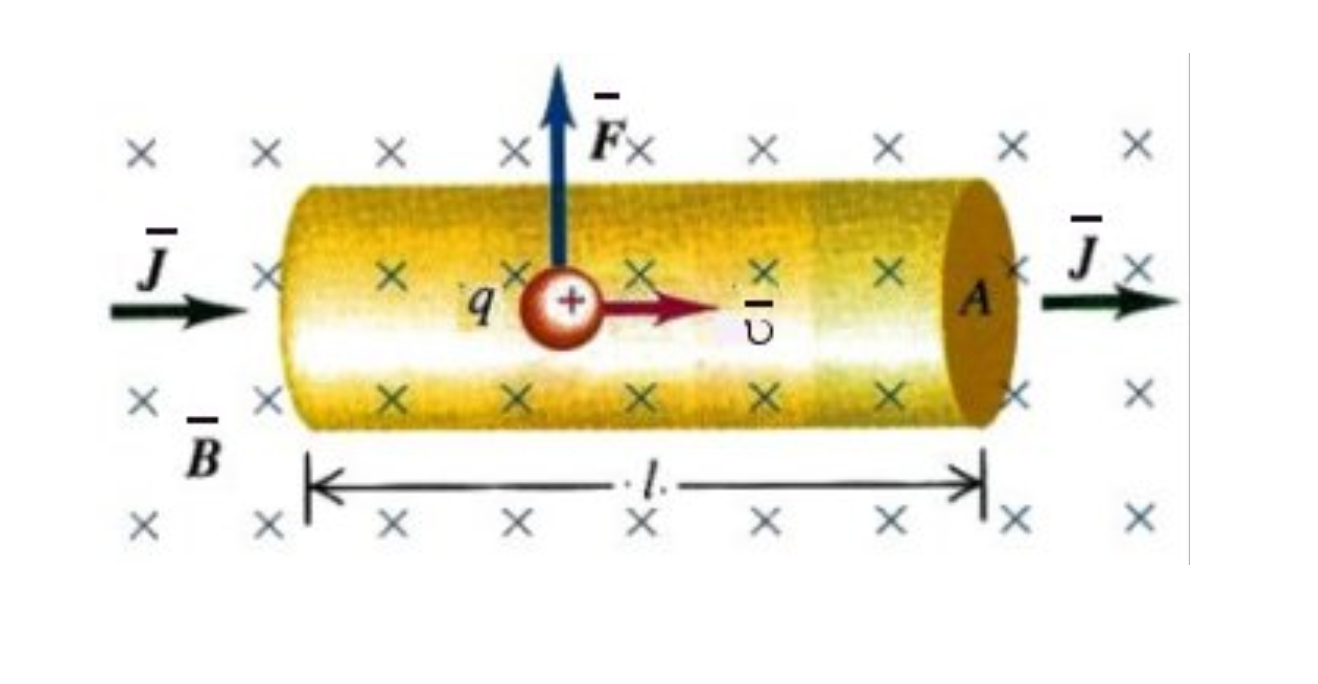
  (3)

В итоге полная сила, действующая со стороны электромагнитного поля на движущуюся относительно избранной системы отсчета заряженную частицу описывается формулой

(4)

Эту силу называют силой Лоренца.

По действию силы на заряженную частицу можно в принципе определить векторы электрического и магнитного полей. Следовательно, выражение для силы Лоренца (4) можно рассматривать как определение электрического и магнитного полей (векторов и ).

В самом деле, измерив ускорение движущейся заряженной частицы массой m, определим полную электромагнитную силу по второму закону Ньютона(электрическая и магнитная составляющие электромагнитной силы относятся к одной и той же системе отсчета. Более того, эта система отсчета должна быть инерциальной, иначе пришлось бы учитывать силы инерции):   . Далее, остановив частицу и измерив силу , действующую на неподвижный заряд q в той же самой точке пространства, например с помощью динамометра, определим как напряженность электрического поля    , так и вектор магнитной силы   . Затем, испытывая все возможные направления движения, найдем такое, двигаясь вдоль которого частица не подвергается действию магнитной силы, - это и есть направление вектора индукции магнитного поля в данной точке пространства. При этом не должно смущать то обстоятельство, что процедура испытания различных направлений движения может потребовать много времени. Дело в том, что рассматриваемый эксперимент скорее мысленный, чем лабораторный, хотя в принципе его можно осуществить и в лаборатории.

Теперь пусть частица движется со скоростью , перпендикулярной к направлению вектора . Умножим векторно слева на выражение (1), записанное для такого случая:

  

Учитывая здесь известное тождество векторной алгебры   , а также соотношения и    , найдем окончательно

  (5)

Отметим, что выражение для электромагнитной силы (4) остается справедливым для переменных полей и произвольных значений скорости заряда .

Аналогично электрическому полю векторов поле магнитной индукции может быть геометрически наглядно представлено с помощью линий поля, проведенных так, что касательная к этим линиям в каждой точке совпадает с направлением вектора индукции , а густота линий пропорциональная модулю вектора в данном месте. Однако магнитное поле в отличие от электростатического устроено так, что изобразить его с помощью линий поля не всегда возможно.

ИЛЛЮСТРАЦИИ. Картину магнитной индукции можно наблюдать с помощью мелких железных опилок, которые в магнитном поле намагничиваются и, подобно маленьким магнитным стрелкам, ориентируются вдоль линий индукции.

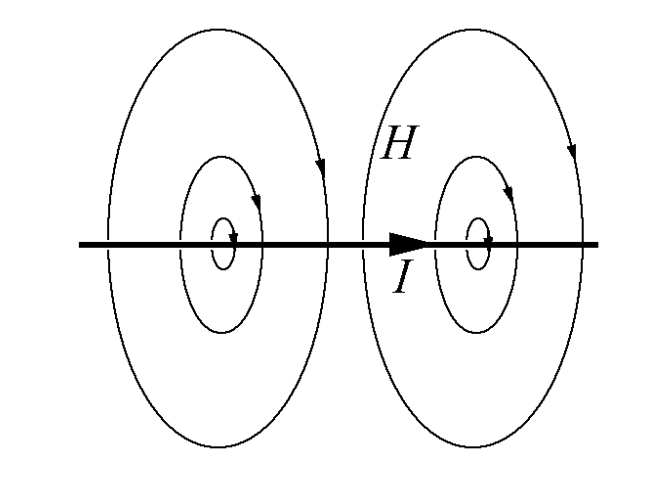
1. Линейный ток

2. Виток с током.

Пример линий магнитной индукции полей постоянного магнита и катушки с током приведен на рис. 

Рисунок Линии магнитной индукции полей постоянного магнита и катушки с током. Индикаторные магнитные стрелки ориентируются по направлению касательных к линиям индукции

Обратите внимание на аналогию магнитных полей постоянного магнита и катушки с током.

Вообще мы увидим, что линии в простых случаях замкнуты (если не уходят на ).Это означает, что магнитное поле не имеет источников – магнитных зарядов. Поля, в которых возможны замкнутые силовые линии (таково поле ), кратко называют соленоидальными или вихревыми, в противоположность потенциальным полям, типа электростатического.

Однако не следует думать, что силовые линии магнитного поля всегда замкнуты. Это распространенное заблуждение, проникшее даже в учебники. Замкнуты линии , например, у кольцевого витка с током I (рис.). Но если пропустить через виток провод с малым током i, добавится малое поле h, перпендикулярное начальному Н. Силовая линия суммарного поля станет спиралью, бесконечно навивающейся на кольцо, и замкнуться может только случайно. При «общем» соотношении токов и при произвольной их геометрии практически все линии будут незамкнуты, причем вполне заметно. Рис.