1.4. Приложения к теории вероятностей.

Развитые в предыдущих разделах методы подсчета позволяют решать задачи теории вероятностей с конечным множеством равновероятных исходов.

Задачи подобного типа особенно часто возникают в теории азартных игр, и не будет преувеличением сказать, что сама теория вероятностей возникла из анализа шансов при игре в кости.

Для решения подобных задач используется классическое лапласовское определение, согласно которому вероятность события А есть отношение числа элементарных исходов, благоприятствующих событию А, к полному числу возможных элементарных исходов:

.

Пусть требуется найти вероятность Р(А) того, что при бросании одной кости выпадет не менее 5 очков. Множество возможных исходов состоит из 6 элементарных исходов, из которых событию А благоприятствуют два: 5 и 6. Поэтому искомая вероятность равна

Пусть теперь требуется найти вероятность Р(А) того, что при бросании двух игральных костей выпадет не более 5 очков. Теперь множество возможных элементарных исходов включает 6^.6=36 элементов, из которых 6 благоприятствуют событию А: (1,1), (1,2), (2,1), (2,2), (2,3), (3,2). Поэтому искомая вероятность равна

Большое число дискретных задач теории вероятностей может быть сформулировано в терминах следующей модели. Из урны, содержащей шаров,– красных и–– синих, вынимаетсяшаров. Какова вероятность, что среди них будеткрасных и–синих шаров?

.

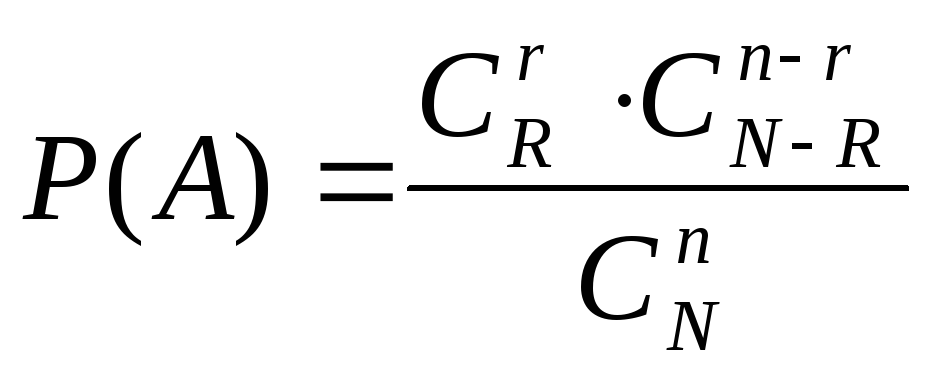Вот пример на применение данной формулы. В лотереи из 49 номеров 6 являются выигрышными. Какова вероятность, что среди 6 отмеченных номеров окажется ровно 4 выигрышных?

Другой пример на урновую модель. Два одинаково метких игрока Петр и Иван состязаются в стрельбе по мишени. Условия состязания таковы, что Петр делает 5 выстрелов, а Иван 10. Победа присуждается Ивану, если ему принадлежит оба из 2 ближайших к центру мишени выстрелов, и Петру – если среди этих двух есть хотя бы один его выстрел. Найти вероятность победы для каждого из участников.

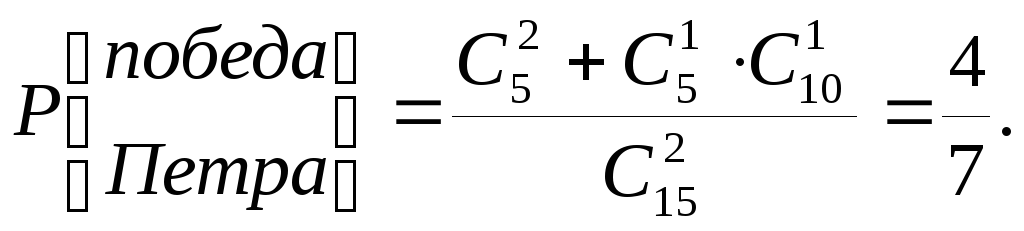
Если из – элементного множества берется случайная– элементная выборка, то полное число элементарных исходов равно, если порядок выбираемых элементов имеет значение, и- если порядок безразличен. В качестве примеров рассмотрим случайные извлечения карт. Предполагая, что используется стандартная колода из 36 карт.

Из перетасованной колоды последовательно тянутся 3 карты. Какова вероятность, что эти 3 карты будут семерка, дама, туз в заданном порядке?

Из перетасованной колоды извлекаются 4 карты. Какова вероятность что будут извлечены 2 короля и 2 дамы?

Какова вероятность при игре «в подкидного дурака» получить при сдаче 4 туза?

т.к. 4 туза дополняются 2 картами, выбранными из остальных 32 карт.

Какова вероятность при игре «в подкидного дурака» получить при сдаче все козырные карты? В этой задаче в элементарный исход наряду с мастью полученными при сдаче картами должна быть включена также и карта, указывающая козырную масть. Поэтому число элементарных исходов равно . Чтобы найти число элементарных исходов, благоприятствующих данному событию, будем считать, что сначала выбирается козырная масть (4 возможности), затем в ней выбирается указывающая козырную масть открываемая карта и, наконец, из оставшихся 8 карт масти выбираются 6 сдаваемых карт. Поэтому искомая вероятность равна

Какова вероятность, что среди 6 полученных при сдаче карт будут присутствовать все масти. Здесь число благоприятствующих исходов находится с помощью формулы включения и исключения.

Много содержательных вероятностных интерпретаций можно дать рассмотренной в предыдущем разделе задаче о беспорядках. Например, мужчин сдают свои шляпы в гардероб и получают их обратно случайным образом. Какова вероятность, что ни на ком не будет одета его собственная шляпа? В другой интерпретации,супружеских пар пришли на танцевальный вечер, где танцевальные пары составляются по жребию. Какова вероятность, что ни одна супружеская пара не будет танцевать вместе? В этой задаче полное число элементарных исходов равно числу перестановок, т.е.!, поэтому искомая вероятность есть

,

и с ростом она стремится к.

Тест.

1. Из конфетницы, содержащей 4 шоколадных конфеты и 8 карамелей, наугад берутся 2 конфеты. Какова вероятность, что обе они шоколадные? а) ; б); в).

2. Из перетасованной 36 – карточной колоды берутся 3 карты. Какова вероятность, что среди них не будет тузов? а) ; б); в).

3. Колода из 36 карт случайным образом делится на пополам. Какова вероятность, что в каждой половине будет по 2 туза? а) ; б); в).

4. Найти вероятность того, что среди 6 карт, полученных при раздаче в игре в «подкидного дурака», не будет ни одного козыря. а) ; б); в).

5. Из 8 букв разрезной азбуки составляется слово «Институт». Затем карточки с буквами перемешиваются и снова собираются в произвольном порядке . Какова вероятность, что снова получится слово «институт»? а) ; б); в).