Глава I. Перечислительная комбинаторика.

1.1. Перестановки, размещения, сочетания и разбиения.

Число перестановок на символах, обозначаемоеP_n, - это число способов введения линейного порядка на множестве из n элементов. Можно сказать, что это число способов расставить n человек в очередь. На первое место можно поставить любого из , на второе – любого из оставшихсяи т.д. пока не дойдем до– го места, на которое останется единственный представитель. Поэтому

Запомним, что

Вот 6 возможных порядков на множестве из 3 элементов :

Пусть из n элементов требуется выбрать m элементов и линейно их упорядочить. Обозначая число таких упорядоченных выборок черези рассуждая, как и прежде, получаем

.

Число называют числом размещений изпо.

Пусть теперь из – элементного множества просто выбирается его– элементное подмножество без упорядочивания. Число– элементных подмножеств– элементного множества обозначается через(читается, «це» изn по m) и называется числом сочетаний из по. Для нахождениязаметим, что упорядоченную выборку можно рассматривать как получаемую в два этапа: сначала из- элементов выбирается неупорядоченное– элементное подмножество, что можно сделатьспособами, а затем выбранное– элементное подмножество линейно упорядочивается, что можно сделатьспособами. Это приводит к соотношению:

,

откуда получаем

.

Заметим, что ,

а также .

Тренер футбольной команды, желающий сделать одновременную замену 2 из 10 полевых игроков и имеющий 5 футболистов на скамейке запасных, может это сделать

способами.

Если футбольный матч закончился в ничью и его судьба решается в серии послематчевых пенальти, то у тренера возможностей представить судье список 5 пенальтистов из 11 закончивших матч футболистов, т.к. порядок выполнения футболистами пенальти имеет значение.

Число различных последовательностей длины , состоящих изсимволов,равно, т.к. на каждое место можно независимо ставить любой изm символов. В частности, число целых неотрицательных не более чем – значных десятичных чисел равно. Пусть теперь задано, что символвстречаетсяраз. Чему равно число последовательностей изm символов с заданным числом включения каждого символа?

Возьмем символовсимволовсимволов, всегоn символов, и занумеруем их числами от 1 до . Тогда каждой перестановке из чисел от 1 доn будет соответствовать последовательность, включающая раз символраз символи т.д. Однако перестановки внутри множеств, соответствующих одинаковым символам, приводят к той же самой последовательности. Отсюда получаем, что число последовательностей равно. В частности, число двоичных последовательностей длинысединицами равно.

Пусть теперь имеется различных типов элементов, причем элементы одинакового типа считаются неразличимыми, а запас элементов каждого типа неограничен. Требуется составить – элементное множество, используяn типов элементов, причем элементов каждого типа может включаться в множество любое число от 0 до . Число таких множеств называется числом сочетаний с повторениями изпои обозначаются. Здесь возможен случай и .

В качестве примера рассмотрим следующую задачу. В магазине имеется 4 сорта роз: красные, желтые, оранжевые, белые. Сколькими способами может быть куплено 5 роз? В наших обозначениях это число равно .

В качестве другого примера рассмотрим целочисленные неотрицательные решения уравнения

связывая с каждой переменной тип элемента, а с её значением – число элементов данного типа, получаем, что число искомых решений равно .

Для того, чтобы найти число , рассмотрим последовательности длиныиз двух символов «*» и «׀», у которых число звездочек равно , а число черточек –. С каждой такой последовательностью можно связать сочетание с повторениями, ставя в каждом изпромежутков между черточками вместо звездочек символы типа, соответствующего номеру промежутка. Этим устанавливается взаимно однозначное соответствие между– элементными множествами изтипов элементов и последовательностями из двух символов. Поэтому

Пусть теперь – элементное множество разбивается наподмножеств. Причемподмножеств имеют мощность,подмножеств – мощностьи т.д., наконец,подмножеств – мощность_.Сколько существует таких разбиений?

С каждой перестановкой исходного - элементного множества можно связать разбиение на подмножества заданной мощности, если в перестановке отсчитывать слева направораз поэлементов,раз поэлементов и т.д. При этом перестановка элементов внутри каждого множества, а также перестановка множеств одинаковой мощности между собой не меняют разбиения. Поэтому число разбиений равно

Пусть в турнире участвуют команд. Сколькими способами может быть проведен первый круг, т.е. сколькими способами команды могут быть разбиты на пары? В соответствии с полученной формулой это число равно

Тест.

1. Сколькими способами может быть выбрано 5 номеров из 36? а) ; б); в)

2. Пусть имеется n языков. Сколько нужно издать словарей, чтобы был возможен перевод с любого языка на любой? а) 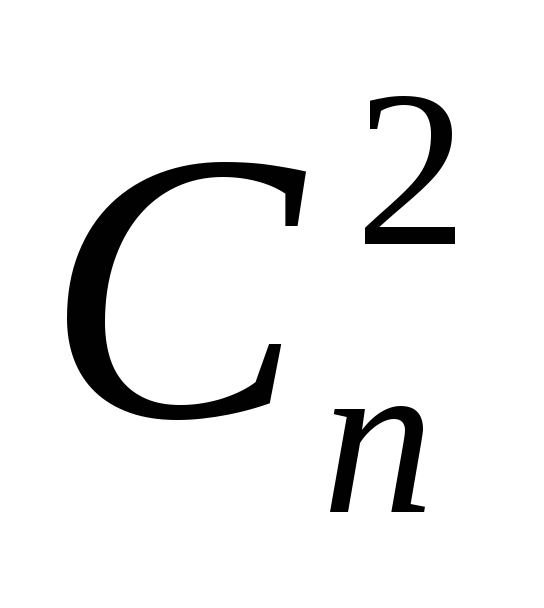; б); в).

3. У мамы 5 яблок, 7груш и 3 апельсина. Каждый день, в течение 15 дней, она выдает сыну по одному фрукту. Сколькими способами это может быть сделано? а) ; б); в).

4. В распоряжении имеются яблоки, груши и апельсины. Сколькими способами может быть составлен подарочный набор из 5 фруктов? а) ; б); в).

5. Сколькими способами можно разделить яблоко, грушу, апельсин, сливу, лимон и айву между тремя мальчиками так, чтобы каждому досталось по 2 фрукта? а) ; б); в).