Лекция 10

3.9.4. Метод половинного деления.

Метод деления отрезка пополам всегда приводит к искомому результату, но иногда он требует значительного объема вычислительной работы. Поэтому обычно его используют, когда возникают трудности с оценкой погрешности в других методах.

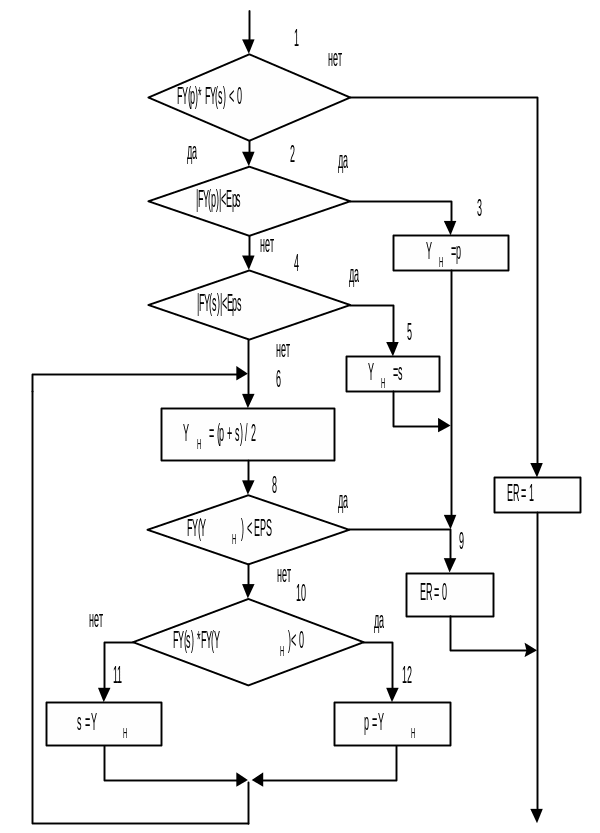
Рис.3.10.1.

Суть метода половинного деления заключается в следующем. Разделим отрезок [ p, s ], на котором ищем корень, пополам, т.е. возьмем и проверим, если | F(y_H) | <=Е_З, то корень уравнения найден. Если же |F(y_Н)| >Е_З, то выберем тот из отрезков [а,у_Н] или [у_Н, b], на концах которого функция F(y) имеет противоположные знаки, и снова разделим его пополам. Этот процесс повторяется до тех пор, пока текущая погрешность не станет меньше заданной. Очевидно, что до начала решения надо убедиться, что корень уравнения располагается на отрезке [ p, s ]. Фрагмент алгоритма решения уравнения методом половинного деления приведен на рис.3.10.1.

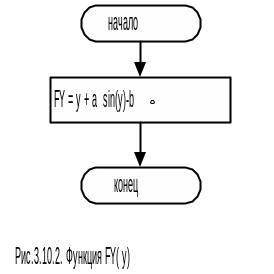
В данном случае целесообразно вычисление функции F(Y) оформить в виде подпрограммы-функции (FY() на рис.3.10.1) с одним фактическим параметром – значение Y, для которого надо вычислить значение функции. Достоинством такого способа вычисления значения функции является высокая степень общности алглритма – для решения того или иного уравнения достаточно записать это уравнение в одном месте – в подпрограмме функции FY. Например, если надо решать уравнение

,

то алгоритм подпрограммы FY будет иметь вид приведенный на рис.3.10.2. При этом предполагается, что параметры а и b уравнения передаются в подпрограмму как глобальные переменные.

В алгоритме рис.3.10.1 сначала осуществляется проверка (блок 1) существования корня на интервале [ p, s ] – для этого произведение функций на концах интервала должно быть отрицательным. Если произведение функций положительно, то признак ER получает значение 1 и осуществляется выход из алгоритма. Значение ER=1 соответствует ситуации "Корень вне заданного интервала". Затем осуществляется проверка значений функции на концах интервала (блоки 2,4). Далее организован циклический процесс деления отрезка [ p, s ] пополам.

3.9.5. Метод Ньютона.

Метод Ньютона обладает более высокой скоростью сходимости по сравнению с другими методами При решении на ЭВМ уравнения вида F(y) = 0 также задают начальное приближение Ун и последовательно вычисляют следующие приближения. Расчет очередного приближения проводится по формуле

где — производная по .

После каждой итерации оценивают текущую погрешность рассмотренным выше способом. Начальное приближение в методе Ньютона целесообразно выбирать так, чтобы выполнялось условие

,

иначе сходимость метода не гарантируется. Обычно выбирают или ( и — границы отделения корней) в зависимости от того, в какой точке выполняется указанное выше условие.

3.9.6. Метод хорд.

В отличие от метода деления отрезка пополам в данном методе в качестве нового приближения к корню уравнения принимаются значения точек пересечения хорды (прямой, соединяющей ординаты у на концах интервала, внутри которого разыскивается корень уравнения) с осью абсцисс. Для точки пересечения хорды с осью абсцисс имеем

где и — концы интервала отделения корней. После вычисления по формуле (2.9) выполняется проверка текущей погрешности. Если |F( )|<=Е_З, то полученное значение принимаем за корень уравнения, если же |F( )|>Е_З, то выбираем тот из отрезков [а, ] или [ ,b], на концах которого функция F(y) имеет противоположные знаки, и снова определяем точку пересечения хорды с осью абсцисс с помощью соотношения (2.9).