Арифметична (лінійна)

Лінійна апроксимація - це пряма лінія, що найкраще описує набір даних. Вона застосовується в найпростіших випадках, коли точки даних розташовані близько до прямої. Кажучи іншими словами, лінійна апроксимація гарна для величини, яка збільшується або зменшується з постійною швидкістю.

Формула:

де m - кут нахилу і b - координата перетину осі абсцис.

У наведеному нижче прикладі лінійне наближення показує рівномірне збільшення обсягу продажів холодильників протягом 13 років. Слід зауважити, що значення R-квадрат у даному випадку становить 0,9036. Це свідчить про досить хорошому узгодженні лінії апроксимації за фактичними даними.

Логарифмічна

Логарифмічна апроксимація добре описує величину, яка спочатку швидко зростає або спадає, а потім поступово стабілізується. Описує як позитивні, так і негативні величини.

Формула:

де c і b - константи, ln - функція натурального логарифма.

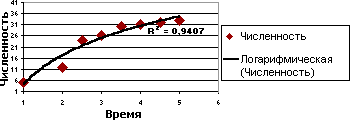
Наведений нижче приклад використовує логарифмічне наближення для ілюстрації прогнозованого зростання популяції тварин на обмеженій території. У міру того як вільного простору стає все менше, темпи зростання популяції також знижуються. Слід зауважити, що значення R-квадрат у даному прикладі дорівнює 0,9407; це вказує на те, що апроксимуюча крива описує дані з досить високою мірою достовірності.

Поліноміальна

Поліноміальна апроксимація використовується для опису величин, що поперемінно зростають і спадають. Вона корисна, наприклад, для аналізу великого набору даних про нестабільну величину. Степінь полінома визначається кількістю екстремумів (максимумів і мінімумів) кривої. Поліном другого ступеня може описати тільки один максимум або мінімум. Поліном третього ступеня має один або два екстремуми. Поліном четвертого ступеня може мати не більше трьох екстремумів.

Формула:

де b і - константи.

Нижче на прикладі апроксимації поліномом другого порядку (одна вершина) показана залежність швидкості від споживання палива. Слід зауважити, що значення R-квадрат у даному випадку становить 0,9474. Це досить добре узгоджується з фактичними даними.

Степенева

Степеневе наближення дає гарні результати, якщо залежність, яка міститься в даних, характеризується постійною швидкістю росту. Прикладом такої залежності може служити графік прискорення автомобіля. Якщо в даних є нульові або негативні значення, використання статечного наближення неможливо.

Формула:

де c і b - константи.

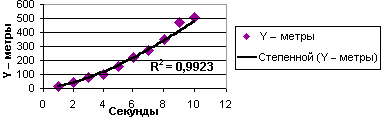
Нижче показаний приклад залежності пройденого шляху від часу (в секундах). Зі ступеневої лінії тренду добре видно збільшення прискорення. Зверніть увагу, що значення R-квадрат у даному прикладі дорівнює 0,9923. Це говорить про високу точність використовуваного наближення.

Експоненціальна

Експоненційне наближення слід використовувати в тому випадку, якщо швидкість зміни даних безперервно зростає. Однак для даних, які містять нульові або негативні значення, цей вид наближення непридатний.

Формула:

де c і b - константи, e - основа натурального логарифма.

На наведеному нижче прикладі експоненціальне наближення ілюструє процес розпаду вуглецю 14. Слід зауважити, що значення R-квадрат тут дорівнює 1, тобто лінія наближення ідеально відповідає даним.