Вариант 3.

1. Выполните задания № 1- 10.3 из практической работы.

2. Предприятие выпускает ежесуточно 8 видов изделий, основные производственно-экономические показатели которых приведены в таблице:

Вид изделия	Количество изделий	Расход сырья, кг/изд	Норма времени изготовления, ч/изд	Цена изделия, ден.ед /изд
1	34	5	10	60,00 грн.
2	123	8	9	45,00 грн.
3	32	2	6	100,22 грн.
4	44	4	14	62,50 грн.
5	12	6	8	80,00 грн.
6	20	12	4	75,10 грн.
7	35	9	12	95,00 грн.
8	20	10	15	60,00 грн.
	вектор ассортимента	вектор расхода сырья	вектор затрат рабочего времени	ценовой вектор
	q	s	t	p

Определить следующие ежесуточные показатели:

1) расход сырья S; S = q ×s

2) затраты рабочего времени T; T = q × t

3) стоимость выпускаемой продукции P. P = q × p

3. Предприятие выпускает 6 видов изделий с использованием 6 видов сырья. Нормы расхода сырья и план выпуска изделий приведены в таблице:

Вид изделия	Нормы расхода сырья						План выпуска
	1	2	3	4	5	6
1	10	3	5	4	2	2	100
2	5	4	2	1	3	5	120
3	1	2	9	2	7	6	80
4	8	5	1	6	1	2	65
5	2	7	4	1	8	4	36
6	1	4	10	7	4	1	40

Определить затраты сырья каждого вида: Q = q^TA

4. В таблице приведены данные о дневной производительности 5 предприятий, выпускающих 4 вида продукции с потреблением 3 видов сырья, а также продолжительность работы каждого предприятия в 2009 году и цена каждого вида сырья.

Вид изделия	Производительность предприятий, изд/день					Затраты сырья, ед. веса / изд
	1	2	3	4	5		1	2	3
1	3	9	5	10	12		6	4	1
2	5	2	2	4	3		3	1	4
3	8	6	12	6	5		2	5	2
4	10	9	5	2	6		6	2	5
	Количество рабочих дней в 2009 году						Цена сырья
	175	204	165	135	175		45	60	80

Определить:

1) годовую производительность каждого предприятия по каждому виду изделий;

(b_ij = t_j * a_{ij ,} где t_j-вектор количества рабочих дней, a_ij-матрица производительности предприятий)

2) годовую потребность каждого предприятия по каждому виду сырья;

(сначала необходимо подсчитать матрицу дневного расхода сырья на предприятиях (D=C^TA, где C^T- матрица затрат сырья на единицу изделия, А- матрица производительности предприятий), а затем найти матрицу годовой потребности предприятий в сырье (e_jk = t_j * d_jk, где t_j - вектор количества рабочих дней, d_jk- матрица дневного расхода сырья на предприятиях)

3) годовую сумму кредитования каждого предприятия для закупки сырья

(G = f*E, где f-вектор стоимости сырья, Е-матрица годовой потребности предприятий в сырье);

4) простой каждого предприятия в 2009 году.

(- сначала подсчитайте количество чистых рабочих дней в 2009 году без учета праздников;

- введите несколько дат, которые будут являться праздниками и подсчитайте количество чистых рабочих дней с учетом праздников;

- подсчитайте вектор вынужденного простоя в 2009 году (h_j = WD - t_j, где WD- количество чистых рабочих дней с учетом праздников, t_j,- вектор количества рабочих дней в году))

5. Отрасль состоит из 4 предприятий, выпускающих по одному виду продукции. Каждое из предприятий отрасли для обеспечения своего производства потребляет часть продукции, выпускаемой им самим и другими предприятиями. Объем продукции и доли потребления продукции предприятиями задаются таблицей:

Продук-ция	Предприятия (доля потребления)				Объем продукции
	1	2	3	4
1	0,8	0,2	0,4	0,45	800
2	0,78	0,86	0,35	0,64	1000
3	0,21	0,54	0,26	0,9	260
4	0,1	0,3	0,78	0,88	640

Определить количество каждого вида продукции, предназначенное для реализации вне данной отрасли (объем конечного продукта).

(Вектор объема конечного продукта можно представить в виде: или в виде y = М*x, M = E – A, где Е – единичная матрица, х – вектор объема продукции.)

6. Предприятие выпускает 5 видов продукции, используя сырье 5 видов. Необходимые характеристики производства указаны в таблице:

Вид сырья	Расход сырья по видам продукции, вес. ед./изм.					Запас сырья, вес.ед.
	1	2	3	4	5
1	4	3	4	2	8	4200
2	2	5	2	3	1	1200
3	1	2	8	5	4	1000
4	5	6	6	1	2	3100
5	6	1	1	4	2	4200

Требуется определить объем выпуска продукции каждого вида при заданных запасах сырья.

(Вектор плана выпуска продукции определяется как решение системы уравнений:

С; Cx = q; x = C^-1 q; где С – матрица расхода сырья по видам продукции, - определитель матрицы С, q - вектор запасов сырья.)

7. Решить системы линейных уравнений АХ=В, А²А^ТАХ=В и вычислить значение квадратичной формы z=Y^TА^ТAA^ТY, где

А= , В= , Y=

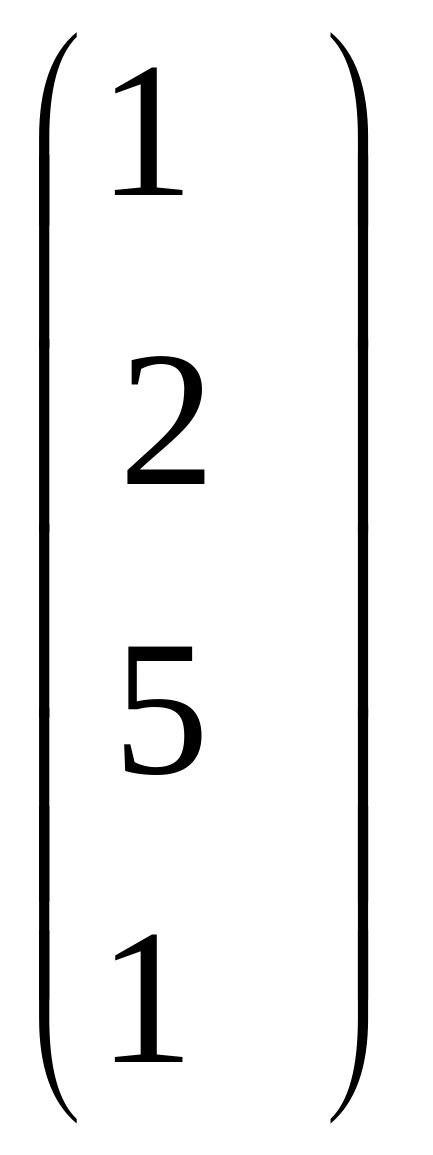
8. Решите методом Гаусса следующую систему линейных уравнений:

х₁+2х₂+3х₃+х₄=3

х₁+4х₂+5х₃+2х₄=2

2х₁+9х₂+8х₃+3х₄=7

3х₁+7х₂+7х₃+2х₄=12

9. Найти все корни уравнения х³+2,84х²-5,6064х-14,766336=0