Запитання для самоконтролю

1. Що називається функцією двох змінних ?

2. Що називається областю визначення функції і її геометричний зміст ?

3. Дати означення функції трьох змінних , n змінних ?

4. Навести приклади функцій двох змінних , трьох змінних .

5. Чи завжди область визначення функції можна зобразити геометрично ? Наведіть приклади .

§5. Границя і неперервність функції

1. Неперервні функції, їх властивості. Число А називається границею функції y=f(x) при х→х₀ , якщо

108

Уся статистична сукупність , з якої відбирається частина для дослідження , утворює генеральну сукупність .

Об’єкти довільно відібрані із генеральної сукупності , утворюють вибірку .

На практиці статистичне дослідження проводять за певними характеристиками або ознаками . Так , у дослідженнях соціологів зустрічаються такі ознаки , як професія , вік , стан матеріального забезпечення . Ознаки поділяють на якісні і кількісні .

Якісні ознаки досліджуваний об’єкт може мати , а може не мати . Вони не піддаються безпосередньому вимірюванню ( напр.: спеціальність , кваліфікація , національність і т. д.)

Кількісні ознаки є результатом вимірювання або підрахунку. Вони поділяються на дискретні і неперервні

Кількісні дискретні ознаки можуть набувати окремих значень із деякої послідовності чисел ( напр.: кількість балів , кількість студентів і т. д.) .

Кількісні неперервні ознаки можуть набувати будь-яких значень у певному інтервалі ( напр.: швидкість руху і т.д.).

У результаті статистичного експерименту над масовими явищами отримують деякий матеріал . Без систематизації та узагальнення розрізнених відомостей у ньому дуже важко розібратися . Тому виникає необхідність представити результат дослідження у вигляді таблиць .

Наприклад , запишемо у вигляді таблиці результати виконання студентами групи РП-11 контрольної роботи з математики .

12

8.Основні поняття математичної статистики.

Термін статистика походить від латинського слова « status » - cтан , становище . Вперше термін статистика був запроваджений Готфрідом Ахенвелем у 1743 році. Він означав сукупність знань про державу , її устрій , чисельність населення, війська .

Сучасна теорія математичної статистики була побудована на початку ХХ століття . Значний внесок у розвиток цього розділу математики зробили українські математики В. Я. Буняковський ( 1804 – 1889 ) та М. П. Кравчук ( 1892 – 1942) .

Статистика – це наука , що збирає , обробляє та вивчає різні дані , які пов’язані з масовими явищами , процесами , подіями .

Сучасна математична статистика поділяється на дві широкі галузі : описову та пояснювальну . Добір потрібної для різних фахівців інформації - справа описової статистики . Як приклад можна навести збір для медичних установ даних про кількість тих , хто захворів на грип у м. Чернівці взимку 2009 – 2010 р.

Коли на основі статистичних результатів описової статистики роблять висновки , будують прогнози , приймають рішення , то застосовують пояснювальну статистику . Наприклад , на основі описової статистики приймається рішення з приводу оголошення карантину в школах у зв’язку з хворобою на грип .

Усі статистичні дослідження можна умовно поділити на такі етапи :

1. Формулювання завдання дослідження та визначення обсягу елементів експерименту.

2. Збирання необхідних даних та їх систематизація .

3. Обробка статистичного матеріалу та його вивчення . Формулювання висновків.

13

для будь-якого додатного числа можна вказати такий окіл точки х₀ , що для всіх х≠х₀ із цього околу виконується нерівність < . Пишуть .

При обчисленні границь користуються наступними правилами: якщо існують і , то

1)

2) де к− стала ;

3)

4) 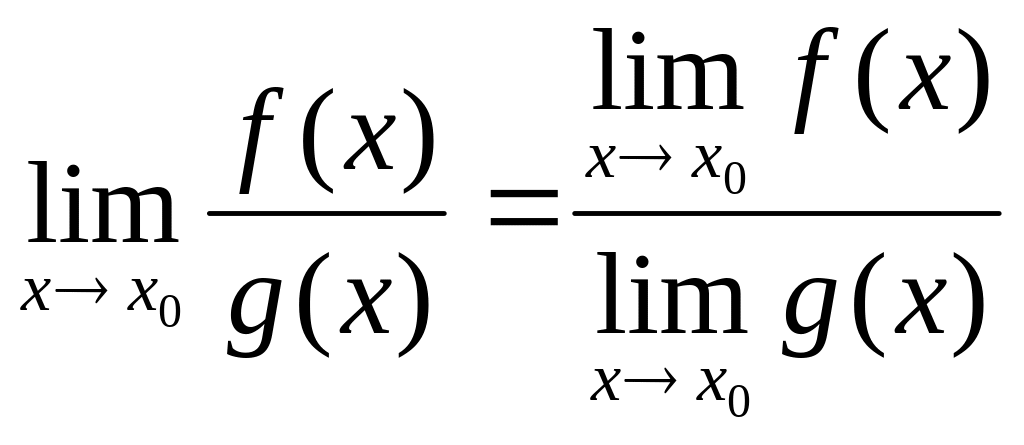при умові , що .

Для розкриття деяких невизначеностей можна скористуватися наступними «чудовими» границями :

; ; = ℮ (℮ = 2,71…)

Функція y=f(x) називається неперервною в точці х₀ , якщо: а) вона визначена в цій точці; б) існує границя ; в) ця границя дорівнює значенню функції в точці х₀.

Функція, неперервна в кожній точці проміжку, називається неперервною на цьому проміжку. Якщо неперервність функції порушується в деякій точці, то цю точку називають точкою розриву функції.

Степенева, показникова, логарифмічна, тригонометрична функції неперервні в своїх областях визначення.

107