§ 17. Ряд Тейлора

Ряд Тейлора має вигляд:

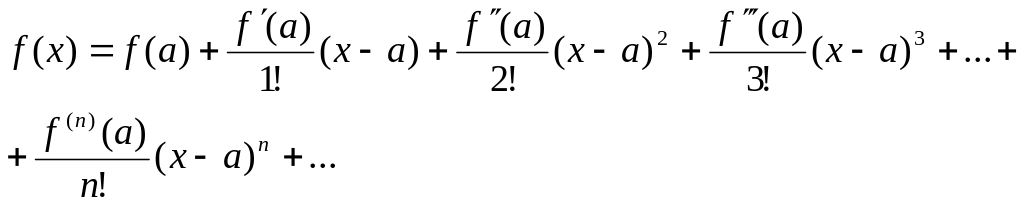(1)

При а=0 маємо ряд Маклорена

(2)

Для розкладу деякої функції f(x) в ряд Маклорена потрібно обчислити значення функції і всіх її похідних при а=0, написати ряд (2) і довести його збіжність до даної функції.

52

= a₀+ a₁ x + a₂ x² +…+ a_n xⁿ +… (3)

де х─ незалежна змінна , а₀ .а₁ ...,а_n , ...─ дійсні числа, які називаються коефіцієнтами ряду.

Як видно буде із наступної теореми, областю збіжності степеневого ряду може бути вся числова вісь, інтервал або тільки одна точка (х=0).

Теорема 1 (теорема Абеля). Якщо степеневий ряд (3) збігається в деякій точці х₀ , то він збігається абсолютно при всіх значеннях х для яких , 2) якщо ряд (3) розбігається при деякому значенні х₁. то він розбігається при всіх х, для яких .

Теорема 2. Областю збіжності степеневого ряду (3) є інтервал з центром в початку координат.

Означення 5. Інтервалом збіжності степеневого ряду називається такий інтервал (- R; R ), що для довільної точки х , що лежить всередині цього інтервалу, ряд збігається абсолютно, а для точок, що знаходяться поза ним, ряд розбігається. Число R називається радіусом збіжності.

Радіус збіжності ряду (3) визначається по формулі: R=

На кінцях інтервалу питання про збіжність або розбіжність даного ряду вирішується індивідуально для кожного конкретного ряду.

Якщо R=0, то ряд (3) збігається тільки в одній точці х=0. Якщо R=∞, то ряд збігається на всій числовій осі.

Приклад 2. Знайдіть область збіжності ряду:

53

Якщо q≠0, то дане рівняння називається лінійним неоднорідним. При розв’язуванні таких рівнянь використовують метод Бернуллі. Для цього використовують підстановку y=uv , y′=uv′+vu′. Підставляючи у і у′ в рівняння, одержимо: uv′+vu′+p uv=q або

uv′+v(u′+pu)=q.

Виберемо функцію u так, щоб u′+pu=0. Тоді v можна знайти з рівняння uv′=q.

Алгоритм розв’язання

1^о. Зводимо рівняння до виду y′+py=q.

2^о. Використовуючи підстановку y=uv , знаходять y′=uv′+vu′ і підставляють ці вирази в рівняння.

3^о. Групують члени рівняння, виносять одну із функцій v або u за дужки. Знаходять другу функцію, прирівнявши вираз в дужках до нуля і розв’язавши одержане рівняння.

4^о. Підставляють знайдену функцію в вираз, що залишився і знаходять другу функцію.

5^о. Записують загальний розв’язок, підставивши вираз для знайдених функцій u і v в рівність y=uv.

6^о. Якщо потрібно знайти частинний розв’язок, то визначають С із початкових умов і підставляють в загальний розв’язок.

Вправи

84. Розв’яжіть рівняння:

1) у′+ =х² (х≠0); 2) у′=2х-2ху; 3) ху′-3у=х⁴;

4) у′х+2у=х³ (х≠0); 5) (1+x²)y′ - xy=2x;

6) y′ cos x+y sin x=1; 7) (x+1) - 2y=(x+1)⁴.

67

85. Знайдіть частинні розв’язки рівнянь, що задовольняють початковим умовам:

1) у′ - у tgx = y = 0 при х = 0.

2) ху′ + у = х² (х≠0) ; у = 2 при х = 1.

3) у′ - у tgx = y = 0 при х = 0.

4) х у′ - у = х³; у = 1/2 при х = 1.

5) х у′ + у – 2 = 0; у = 2 при х = -1.