Запитання для самоконтролю

1. Дайте означення уявної одиниці.

2. Як обчисляють степені уявної одиниці?

3. Яке число називається комплексним?

4. Які комплексні числа називаються рівними?

5. Які комплексні числа називаються спряженими?

6. Як виконуються додавання, віднімання, множення комплексних чисел в алгебраїчній формі?

7. Як виконується ділення комплексних чисел в алгебраїчній формі?

8. Як геометрично зображаються комплексні числа?

9. Що називається модулем і аргументом комплексного числа? Запишіть їх формули.

10. Як записується комплексне число в тригонометричній і показниковій формах?

11. Як виконуються дії комплексних чисел, записаних в тригонометричній формі, в показниковій формі?

12. Як розв’язати квадратне рівняння, якщо дискримінант його від’ємний?

72

називається визначником третього порядку.

Визначник третього порядку обчисляється за правилом трикутників:

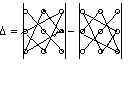
Мінором M_ij елемента a_ij визначників другого і третього порядків відповідно називається визначник першого і другого порядків , які дістаємо з даних визначників викресленням і-го рядка і j-го стовпця .

Алгебраїчним доповненням A_ij елемента a_ij називається його мінор взятий зі знаком (-1)^i+j , тобто

A_ij =(-1)^i+j M_ij

Основні властивості визначників.

1. Визначник не зміниться, якщо його рядки замінити відповідними стовпцями.

2. Якщо переставити місцями два рядки (стовпці), то визначник змінить знак.

3. Якщо один з рядків ( стовпців) визначника складається тільки з нулів , то визначник дорівнює нулю .

4. Якщо визначник має два однакових рядки (стовпці) , то він дорівнює нулю.

5. Спільний множник, що міститься в усіх елементах одного рядка ( стовпця), можна винести за знак визначника .

6. Якщо у визначнику елементи двох рядків ( стовпців ) пропорційні , то визначник дорівнює нулю.

7. Визначник не зміниться , якщо до елементів одного рядка ( стовпця ) додати відповідні елементи іншого рядка ( стовпця ) , помножені на одне й те саме число .

48

110. Розкласти функцію f(x)=5 тільки по косинусах в проміжку (0;5].

Глава 7. Елементи лінійної алгебри

Алгебраїчна символіка була створена в основному в 16-17 ст.

Першим застосував буквенні позначення як для невідомих , так і для заданих в задачі величин , французький математик Ф. Вієт.

До середини 18 ст. алгебра складалася приблизно в тому об’ємі , який нині називають елементарною алгеброю .

Однією з основних задач лінійної алгебри є розв’язування систем лінійних алгебраїчних рівнянь. У зв’язку з вивченням цих систем винили поняття визначника та матриці.

§19. Визначники

Поняття « визначник » ( від латинського determino – визначаю) ввів В. Лейбніц.

Вираз називається визначником (детермінантом ) другого порядку.

Приклад. Обчислити визначник :

Вираз :

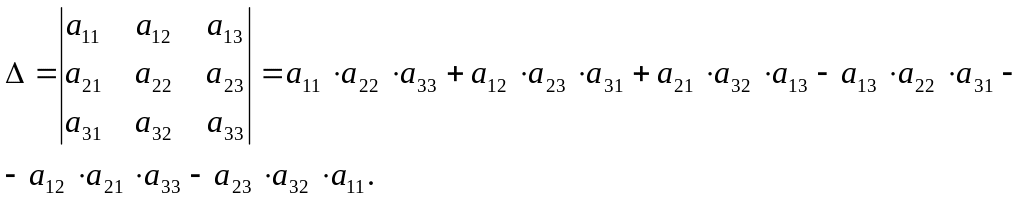
49