
5.3.1. Метод простого перебора
Предположим,
что
.
Строятся точки
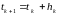 ,
,
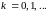 ,
где все
,
где все
 .
Положим
.
Положим
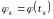 ,
.
Найдем минимальное значение
,
.
Найдем минимальное значение
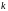 ,
для которого
,
для которого
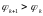 .
Обозначим его через
.
Обозначим его через
 .
Легко увидеть, что метод конечен.
Предположим, что
.
Легко увидеть, что метод конечен.
Предположим, что
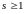 .
Тогда в силу унимодальности функции
отрезок
.
Тогда в силу унимодальности функции
отрезок
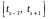 является отрезком локализации.
Заметим, что при этом точки
является отрезком локализации.
Заметим, что при этом точки
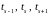 образуют выпуклую тройку. Если же
образуют выпуклую тройку. Если же
 ,
то отрезком локализации является
отрезок
,
то отрезком локализации является
отрезок
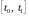 ,
а в качестве выпуклой тройки можно
взять, например, точки
,
а в качестве выпуклой тройки можно
взять, например, точки
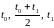 .
.
В случае,
когда
,
точки
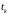 строятся по формуле
строятся по формуле
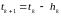 .
.
Варианты
метода простого перебора отличаются
друг от друга выбором шага табуляции
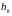 .
В частности, используется формула
.
В частности, используется формула
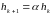 ,
где
,
где
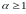 .
Если
.
Если
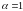 ,
то получаем вариант метода с постоянным
шагом
,
то получаем вариант метода с постоянным
шагом
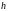 .
Успех применения метода в этом случае
полностью определяется удачным
выбором значения
.
Для ускорения поиска отрезка
локализации, как пра-вило, выбирают
.
Успех применения метода в этом случае
полностью определяется удачным
выбором значения
.
Для ускорения поиска отрезка
локализации, как пра-вило, выбирают
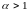 .
Например, если
.
Например, если
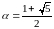 ,
то
,
то
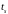 является точкой золотого сечения
отрезка
.
Такой вариант метода отыскания
отрезка локализации удобно сочетать
с последующим применением метода
золотого сечения.
является точкой золотого сечения
отрезка
.
Такой вариант метода отыскания
отрезка локализации удобно сочетать
с последующим применением метода
золотого сечения.
Если же
предполагается использование метода
парабол, то удобно полагать
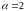 .
В этом случае после нахождения
отрезка локализации
вычисляют точку
.
В этом случае после нахождения
отрезка локализации
вычисляют точку
 .
Из полученных четырёх равноотстоящих
точек выбирают выпуклую тройку. Если
.
Из полученных четырёх равноотстоящих
точек выбирают выпуклую тройку. Если
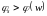 ,
то точки
,
то точки
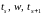 образуют выпуклую тройку, если же
образуют выпуклую тройку, если же
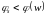 ,
то берутся точки
,
то берутся точки
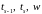 .
Такой прием нахождения начальной
выпуклой тройки используется в методе
Дэвиса, Свенна и Кэмпи
(ДСК).
.
Такой прием нахождения начальной
выпуклой тройки используется в методе
Дэвиса, Свенна и Кэмпи
(ДСК).
5.3.2. Метод дск
В методе
ДСК на основе выпуклой тройки
(найденной по описанному выше правилу)
с помощью метода парабол вычисляется
точка
(минимум квадратного трехчлена), после
чего, если не достигнута заданная
точность, отыскивается новая выпуклая
тройка. Поскольку расположение
искомого минимума
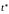 относительно
неизвест-но, поиск осуществляют на
всей числовой оси в соответствии с
описанным выше вариантом мето-да
простого перебора. При этом в качестве
точки
выбирается
,
а начальное значение шага
относительно
неизвест-но, поиск осуществляют на
всей числовой оси в соответствии с
описанным выше вариантом мето-да
простого перебора. При этом в качестве
точки
выбирается
,
а начальное значение шага
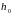 заменяется на
заменяется на
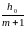 ,
где
,
где
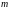 – некоторое натуральное число.
Описанная процедура повторяется до
достижения требуемой точности.
– некоторое натуральное число.
Описанная процедура повторяется до
достижения требуемой точности.
Изложенные в этом параграфе методы предполагают унимодальность функции. Если же минимизируемая функция не унимодальна, то для ее минимизации следует применять другие методы, например, метод ломаных.
