
Методы оптимизации: Часть II
5. _Методы одномерной минимизации
Заключительная глава пособия посвящена методам одномерной минимизации. Задача минимизации функций одной переменной актуальна не только как самостоятельная проблема, имеющая многочисленные приложения, но и как вспомогательная задача в рамках различных методов безусловной минимизации и методов решения задачи нелинейного программирования. Например, задача одномерной минимизации возникает при нахождении полного шага в различных вариантах вышеизложенных методов многомерной оптимизации.
Дадим следующие определения.
Определение
1.
Функция
![]() одного
действительного переменного определенная
на отрезке
одного
действительного переменного определенная
на отрезке
 называется
унимодальной
на
называется
унимодальной
на
 ,
если
существует
точка
,
если
существует
точка
 такая,
что функция
убывает
на
такая,
что функция
убывает
на
 и
возрастает на
и
возрастает на
 .
.
Примером унимодальной функции служит строго выпуклая на функция.
Если унимодальная функция достигает на
точной нижней грани (например, в случае, когда функция непрерывна на ограниченном отрезке
),
то только в точке
![]() .
В этом случае
– это единственный локальный минимум
функции
на отрезке
.
В этом случае
– это единственный локальный минимум
функции
на отрезке
.
Определение 2. Ограниченный отрезок , содержащий единственный локальный минимум функции , называется отрезком локализации.
Легко увидеть, что справедлива следующая теорема.
Теорема 1. Пусть функция унимодальна на отрезке
,
 и
и
![]() .
Тогда,
если
.
Тогда,
если
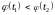 ,
то
,
то
![]() .
Если
же
.
Если
же
 ,
то
,
то
 .
.
Этот факт будет в дальнейшем использоваться в различных методах.
Знакомство с методами одномерного поиска начнем с методов решения задачи минимизации унимодальной функции на отрезке локализации
.
5.1. Метод пассивного поиска
Пусть
![]() – натуральное число, точки
– натуральное число, точки
 .
Обозначим
.
Обозначим
 ,
,
 .
Пусть
.
Пусть
 .
Тогда
в силу унимодальности функции
новым отрезком локализации будет
.
Тогда
в силу унимодальности функции
новым отрезком локализации будет
 ,
если
,
если
 ;
;
 ,
если
,
если
 ;
и
;
и
 ,
если
,
если
 .
В качестве приближённого значения
.
В качестве приближённого значения
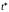 обычно выбирают либо
обычно выбирают либо
 ,
либо середину полученного отрезка
локализации.
,
либо середину полученного отрезка
локализации.
Удобно,
когда в этом методе узлы
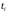 –равноотстоящие, то есть
–равноотстоящие, то есть
 ,
где шаг табуляции
,
где шаг табуляции
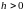 .
В этом случае легко вычислить значение
,
обеспечивающее требуемую точность
(длину полученного отрезка локализации).
.
В этом случае легко вычислить значение
,
обеспечивающее требуемую точность
(длину полученного отрезка локализации).
Таким образом, при пассивном поиске число точек табуляции определяется заранее, и значение функции вычисляется во всех точках. Значение функции в каждой текущей точке не влияет на последующие вычисления.
Существуют методы, где, в отличие от методов пассивного поиска, в ходе вычислений используется ранее полученная информация. Таким методам можно дать общее название методы последовательного поиска.
5.2. Методы последовательного поиска
Большая
группа этих методов основана на следующей
схеме. Строится последовательность
вложенных друг в друга отрезков
локализации
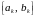 ,
,
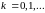 ,
где
,
где
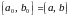 .
Если
.
Если
 ,
то
,
то
 .
На практике знание такой последовательности
отрезков локализации позволяет
локализовать минимум с необходимой
точностью. Например, если задано
некоторое
.
На практике знание такой последовательности
отрезков локализации позволяет
локализовать минимум с необходимой
точностью. Например, если задано
некоторое
 ,
то при
,
то при
 таком, что
таком, что
 ,
любую точку
,
любую точку
![]() отрезка
отрезка
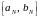 можно
считать приближенным решением задачи.
При этом
можно
считать приближенным решением задачи.
При этом
 .
.
Методы последовательного поиска различаются способами построения последовательности отрезков , В частности, одним из вариантов последовательного поиска является многократное повторение пассивного поиска на получаемых отрезках локализации. Например, ес-
ли
на каждом этапе
![]() полагать
полагать
 ,
то есть
,
то есть
 ,
,
 ,
,
 ,
,
 ,
и
,
и
 ,
то точки
,
то точки
![]() будут делить отрезок локализации на
четыре равные части. Следовательно,
длина нового отрезка локализации
будут делить отрезок локализации на
четыре равные части. Следовательно,
длина нового отрезка локализации
 будет
в 2 (а иногда, возможно, и в 4) раза
меньше длины отрезка
будет
в 2 (а иногда, возможно, и в 4) раза
меньше длины отрезка
 .
.
Положительным
моментом этого метода является
высокая скорость уменьшения длины
отрезка локализации (на каждой итерации
гарантируется ее уменьшение в два
раза). Легко вычислить количество
итераций
![]() ,
необходимое для достижения заданной
точности. Действительно, так как для
любого
выполняется
,
необходимое для достижения заданной
точности. Действительно, так как для
любого
выполняется
 ,
то
–
это наименьшее значение
,
для которого
,
то
–
это наименьшее значение
,
для которого
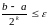 .
Таким образом,
.
Таким образом,
 .
В то же время, отрицательным моментом
этого метода является, то, что на
каждой итерации необходимо к оставшимся
с предыдущей итерации трем точкам
.
В то же время, отрицательным моментом
этого метода является, то, что на
каждой итерации необходимо к оставшимся
с предыдущей итерации трем точкам
 ,
которые теперь обозначим как
,
которые теперь обозначим как
 ,
добавить новые
,
добавить новые
 и вычислить значения функции
и вычислить значения функции
![]() .
.
Далее мы обсудим возможность построения таких схем построения отрезков локализации, ко-торые позволят на каждой итерации добавлять к
уже известным узлам только лишь один новый. Но прежде мы приведем еще одно свойство унимодальной на отрезке функции .
Теорема
1.
Пусть числа
![]() таковы,
что
таковы,
что
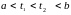 .
Если
.
Если
 ,
то
отрезок
,
то
отрезок
 является
отрезком локализации, если же
является
отрезком локализации, если же
 ,
то
тогда отрезок
,
то
тогда отрезок
 является
отрезком локализации.
является
отрезком локализации.
Это свойство унимодальных функций используется в различных методах одномерного поиска для построения последовательности отрезков локализации. Приведем основанную на теореме 2 принципиальную схему методов минимизации унимодальной функции , для которой известен отрезок локализации
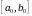 .
.
Пусть
построен отрезок локализации
,
где
Опишем способ нахождения отрезка
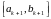 .
Тем или иным способом находятся
числа
такие, что
.
Тем или иным способом находятся
числа
такие, что
 .
Если
.
Если
 ,
то полагаем
,
то полагаем
 .
Иначе полагаем
.
Иначе полагаем
 .
.
Основное различие методов в рамках этой схемы состоит в разных правилах вычисления точек . Во многих из этих методов точки расположены симметрично относительно середины
текущего отрезка локализации. К таким методам
относятся, например, метод дихотомии, метод золотого сечения, метод Фибоначчи и другие.
Остановимся коротко на двух из них.
