2.3. Стаціонарна модель молекулярної дифузії з процесами перетворення речовини.

Установлений процес розповсюдження неконсервативних речовин,або консервативних речовин при наявності джерел їх поповнення, в екосистемі з нерухомим середовищем описується стаціонарним рівнянням молекулярної дифузії, яке у разі лінійної кінетики перетворення речовини записується в такому вигляді:

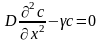(2.41)

Як і раніше , спочатку знайдемо розвязок за умови, що відомі значення концентрації забруднень на краях середовища, тобто виконуються крайові умови:

с(0)=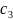 ; с(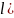 = 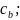(2.42)

Розв’язавши характеристичне рівняння у цьому випадку

D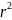 - 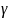=0 (2.43)

маємо :

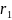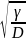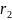=- , = . (2.44)

Отже загальний розв’язок рівняння (2.41) має вигляд:

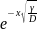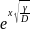c(x)=A + B . (2.45)

Використовуючи граничні умови (2.42),маємо: 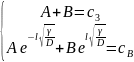(2.46)

Розв’язавши систему рівнянь (1.46) знайдемо невідомі сталі А і В,а саме:

A=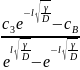 , B=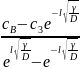 . (2.47)

Підставивши сталі (2.47) в праву частину (2.45) ,шукану математичну модель запишемо в такому функціональному вигляді:

с(х)= + 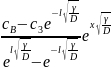(2.48)

або у вигляді:

c(x)=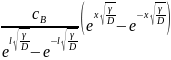 + 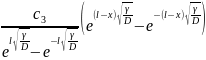(2.49)

Якщо знайти границю виразу (2.49) при y0, то , використовуючи правило Лопіталя = ,

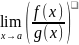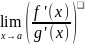одержимо: = + = + = +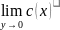

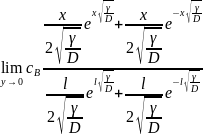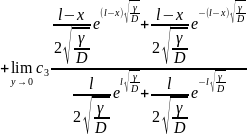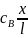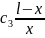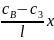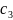
або

с(x)= + .

Остання рівність збігається з одержаним раніше розв’язком (2.9) , що моделює процес молекулярної дифузії без джерел і перетворень (самоочищення). Таке одержання частинного розв’язку із більш загального випадку є підтвердженням правильності побудованих моделей.

Використовуючи означення гіперболічного синуса, а саме:

sh x = 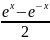, (2.50)

розвязок (2.42) можна записати у досить компактному вигляді:

c(x) =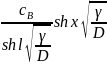 + 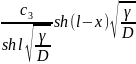. (2.51)

Тепер знайдемо розвязок за умови , що відома концентрація на початку ділянки розповсюдження забруднень , а в кінці ділянки градієнт концентрації дорівнює величині –к , тобто за таких граничних умов:

с(0)= ; 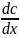|x=l =-k. (2.52)

Загальний розвязок рівняння (2.41) має вигляд (2.45). Використовуючи крайові умови (2.52) , знайдемо сталі А і В у цьому випадку:

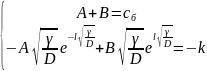(2.53)

A= 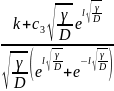, B = 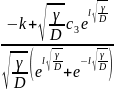(2.54)

Отже шуканий розвязок запишеться у вигляді :

c(x)=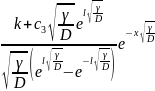 + 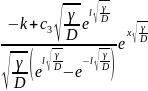(2.55)

Побудовану функціональну модель (2.55) можна записати і в такому вигляді :

c(x)= 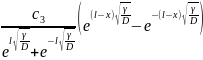+ 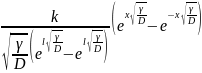. (2.56)

Використовуючи означення гіперболічного синуса (2.50) і гіперболічного косинуса ,

сh x = 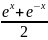, (2.57)

рівність (2.56) можна записати у вигляді :

c(x) =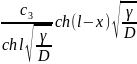 - 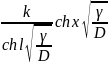. (2.58)

У кінці ділянки шлях розповсюдження речовини закінчується , інакше кажучи, у цій точці градієнт концентрації забруднень дорівнює нулю (к=0).

Отже, у даному випадку процес розповсюдження забруднень описується такою функцією:

c(x) = . (2.59)

Як бачимо, на відміну від розглянутого раніше лінійного закону розповсюдження консервативних речовин, процес розповсюдження неконсервативних речовин відбувається за нелінійним законом.