2.2.Нестаціонарна молекулярна дифузія консервативних речовин

Розглянемо нестаціонарний (неусталений) процес розповсюдження забруднень (або мікроорганізмів) у нерухомому середовищі за відсутності джерел і хімічних або біологічних перетворень (консервативні речовини). Такий процес описується нестаціонарним рівнянням молекулярної дифузії:

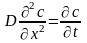, (2.13)

де - коефіцієнт молекулярної дифузії, який визначається природними якостями дифундуючої речовини і середовищем, в якому розповсюджується забруднення.

Розв’язок рівняння в частинних похідних (2.13) визначається однозначно за умови, що він задовольняє додаткові умови, які одержуються на основі спостережень за реальним процесом. Такі умови, як правило, задаються на кінцях ділянки (області), в якій відбувається даний процес.

Додаткові (крайові) умови візьмемо такі: задані значення концентрації забруднення на початку процесу в точці 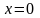і на віддалі від початку в точці , а саме:

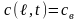, . (2.14)

Крім згаданих додаткових (граничних) умов, потрібно знати ще початковий стан у водоймищі, тобто в момент часу . Якщо в початковий момент часу концентрація забруднень у водоймищі відома, то повинна виконуватись одна з таких додаткових (початкових) умов:

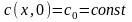, , (2.15)

де – концентрація забруднень в початковий момент часу .

Диференціальне рівняння (2.13) та додаткові (граничні і початкові) умови (2.14) і (2.15) називаються крайовою задачею. Отже, щоб побудувати математичну модель у вигляді функціональної залежності , необхідно розв’язати крайову задачу (2.13) – (2.15), тобто знайти такий розв’язок рівняння (2.13), який би задовольняв граничні (2.14) та початкові (2.15) умови.

Розв’язок крайової задачі (2.13) – (2.15) шукатимемо у вигляді суми:

, (2.16)

де функція – це розв’язок стаціонарної крайової задачі типу (2.2), (2.4), а саме:

, , , (2.17)

що має такий вигляд:

. (2.18)

Невідома функція є розв’язком крайової задачі з нульовими (однорідними) граничними умовами, а саме:

, (2.19)

, , (2.20)

. (2.21)

Розв’язки рівняння (2.19) шукаємо за допомогою методу відокремлених змінних (методом Фур’є) в такому вигляді:

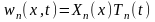. (2.22)

Використовуючи однорідні умови (2.20) та співвідношення (2.22), для функцій 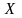і матимемо такі нульові крайові умови:

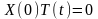, , (2.23)

, . (2.24)

Підставляючи (2.22) в рівняння (2.19), одержимо рівність

,

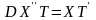з якої після ділення на добуток маємо:

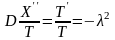, (2.25)

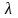
де - довільна стала, яку необхідно визначити.

На основі (2.25),(2.23) і (2.24) можна записати таку крайову задачу для звичайного диференціального рівняння:

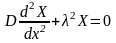, . (2.26)

Тепер потрібно знайти такі значення параметра , за яких існують ненульові розв’язки крайової задачі (2.26), і самі нетривіальні розв’язки. Ці значення параметра називаються власними значеннями, або власними числами, а відповідні розв’язки – власними функціями. Крайова задача (2.26) називається задачею Штурма-Ліувіля.

Характеристичне рівняння і його розв’язки мають такий вигляд:

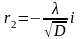, , , . (2.27)

Отже, загальний розв’язок диференціального рівняння запишемо так:

. (2.28)

Використовуючи рівняння (1.28) і граничні умови, одержимо:

. (2.29)

З останнього рівняння знаходимо власні значення:

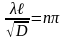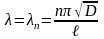, , (2.30)

Враховуючи вирази (2.28), (2.29), (2.30), для кожного власного значення запишемо власні функції – шукані розв’язки крайової задачі (2.26):

. (2.31)

Із співвідношень (1.25) для кожного власного значення одержимо ще одне рівняння:

, (2.32)

частинні розв’язки якого мають такий вигляд:

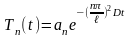. (2.33)

Отже, враховуючи співвідношення (2.22), (2.31) і (2.33) частинні розв’язки рівняння (2.19), що задовольняють нульовим граничним умовам (2.20), запишуться в такому вигляді:

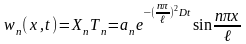, (2.34)

а загальний розв’язок згідно з принципом суперпозиції для лінійних рівнянь має такий вигляд:

, (2.35)

де - поки що невідомі сталі.

Визначимо сталі коефіцієнти ,скориставшись початковими умовами (2.21):

. (2.36)

Помноживши ліву і праву частини рівняння (1.36) на з наступним інтегруванням одержаної рівності, матимемо:

.

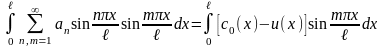Використовуючи ортогональність власних функцій і , маємо:

, ;

.

З останньої рівності знаходимо:

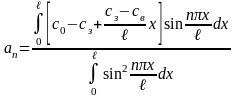. (2.37)

Обчислимо інтеграли в правій частині (1.37), а саме:

1)

.

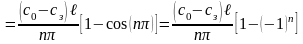2)

.

3) .

Враховуючи 1), 2), 3), вираз (2.37) перепишемо у такому вигляді:

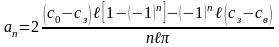
або

.

Остаточно маємо:

. (2.38)

Отже, шуканий розв’язок (2.16) запишеться у вигляді . (2.39)

Зауваження. При розв’язок спрощується і має такий вигляд: , . (2.40)

При з (2.39) або (2.40) одержимо стаціонарний розв’язок (2.9), що не залежить від часу .