Просторові і часові співвідношення

Відносність часових інтервалів

На відміну від перетворень Галілея в перетвореннях Лоренца просторові і часові характеристики ви­являються взаємозв'язаними, і це приводить до досить дивних, на перший погляд, наслідків.

Відносність поняття одночасності

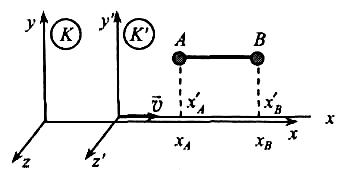
Якщо в системі К (рис. 6.16.) у точках А і В одночасно відбу­лись дві події, то в цій системі інтервал часу між подіями дорівнює нулю:

Δt=t_B – t_A= 0.

Рис. 6.16.

Потрібно б попередньо домовитись, яким чином ми встанови­ли, що події були одночасними в цих, можливо, далеких одна від, одної точках. Найпростіший спосіб — це скористатися сталістю швидкості світла. Встановимо приймач світла точно посередині між точками А і В. Якщо він зафіксує, що світловий сигнал із точ­ки А прийшов одночасно із сигналом з точки В, то це й означати­ме, що події в обох точках відбулися одночасно. Зрозуміло, що си­гнали випускалися в моменти подій.

З точки зору спостерігача в системі К' подія в точці А відбулась у момент часу

,

а подія в точці В – в момент часу

Інтервал часу між подіями в системі К':

Відразу бачимо, що коли Δt = 0, то Δt' може й не дорівнювати нулю через другий член у квадратних дужках. Отже, події, одночасні в одній системі відліку, можуть бути не одночасними в іншій. Звідси випливає висновок: одночасність відносна.

Згідно з формулою можливі випадки, коли події, одночасні в одній системі, будуть фіксуватися як одночасні і в іншій системі:

• х_А=х_В – події відбуваються в тій самій точці,

• υ = 0 – системи відліку нерухомі одна відносно одної,

• с →∞ – сигнал поширюється з нескінченною швидкістю.

Відмінність інтервалів часу між подіями

Розглянемо тепер випадок, коли в системі К події відбуваються неодночасно. Наприклад, подія в точці В відбулася пізніше, ніж у точці А. Інтервал часу в системі К більший за нуль: Δt=t_B – t_A> 0. Інтер­вал часу в системі К' ми щойно записували. Перепишемо його таким чином:

,

де – час, потрібний для того, щоб світло з точки А дійшло до точки В.

Тепер бачимо, що знак Δt′ визначається різницею членів у квадратних дужках, точніше величиною другого члена, в який входить швидкість системи К' відносно системи К. Цілком можливі випадки, коли другий член буде більший, ніж перший, і тоді Δt′ буде менше за нуль. Виходить, що в цій системі спостерігач зафіксує іншу послідовність подій, ніж спостерігач у першій системі.

Виникає якась дивна ситуація. В одній системі відліку відбулися дві події в цілком визначеній послідовності. Наприклад, подія в точці А відбулася раніше, ніж подія в точці В. А спостерігач в іншій системі відліку може зафіксувати або таку саму послідовність подій, або протилежну. Можлива й одночасність. Тут немає ніякої містики, бо будь-які спостереження пов'язані з передаванням сигналів зі швидкістю світла, а вона кінцева. Усі «дива», які дістаємо з перетворень Лоренца, легко пояснюються порівнянням часу поширення світла з однієї точки в іншу та інтервалу часу між подіями.

Якщо подія в точці В є наслідком події в точці А, то вона ніяк не може відбутися раніше, ніж інфор­мація про «подію-причину» дійде до точки В, тобто не раніше, ніж через інтервал часу δt_АВ. Тому Δt завжди більше за і вираз завжди більший за нуль. Висновок: причинно-наслідковий зв'язок не порушується.

Відносність часу

Покажемо тепер відносність самого поняття часу. Нехай у точці А, нерухомій відносно системи К', відбувається низка подій протягом часу t'=t'₂ – t'₁. За цей час точка А відносно системи К зміститься на відстань х₂ – х₁ = υt, бо вона рухається зі сталою швидкістю υ разом із системою відліку К'. Скориста­ємося формулою для зв’язку інтервалів часу:

Оскільки t₂ – t₁= t, то

Звідси випливає, що час у різних системах відліку перебігає по-різному. Час, який відлічується в ру­хомій системі відліку К, буде більшим, ніж у нерухомій, тобто у власній системі відліку К'.

Власний час завжди буде найменшим.

Цей ефект підтверджується розглянутими раніше дослідами з π⁺ -мезонами. Варто наголосити на обо­ротності часу. Якщо в обох системах відбуватимуться події однакової тривалості, то кожному спостерігачеві чужий процес уявлятиметься сповільненим.

Відносність довжини відрізків

Нехай довжина відрізка в системі К' дорівнює l' = х'₂ – х'₁. Визначаючи координати х₂ і х₁ в системі К, знайдемо довжину відрізка в цій системі:

l = х₂ – х_1.

Згідно з перетворенням Лоренцa

і тоді

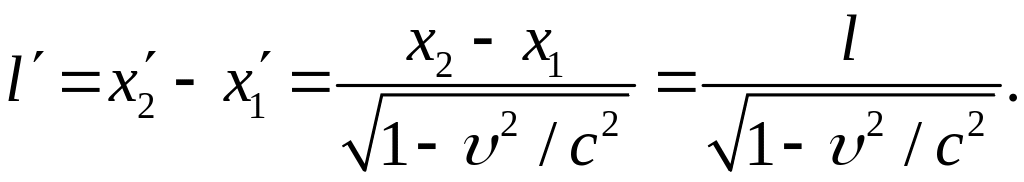
Звичайно здобуту формулу записують так:

Отже, спостерігач, розташований у системі К, побачить відрізок меншої довжини, ніж спостерігач у системі К'.

Довжина відрізка найбільша у власній системі відліку.

Простір-час

Доходимо таких висновків:

– довжина інтервалів часу в різних інерціальних системах відліку різна:

Δt ≠Δt';

– довжина просторових інтервалів у різних інерціальних системах відліку також різна:

Δl ≠Δl';

Тепер згадаємо, що кількість інерціальних систем нескінченно велика і погодимося із сумним висновком про відносність просторових і часових характеристик. Звідси недалеко й до думки про відносність всього сущого або навіть до сумнівів щодо реальності навколишнього світу.

Але ж має бути щось, не змінюване з переходом від однієї випадково вибраної інерціальної системи відліку до іншої, так само випадково вибраної системи? Бо як же можуть фізичні закони бути одними й тими самими в різних системах відліку?

Підказка для пошуку таких незмінних (інваріантних) величин міститься в самих перетвореннях Ло­ренца, в яких «перемішані» просторові і часові характеристики.

Пошуки завершились успіхом, і на сцені з’явився просторово-часовий інтервал або просто інтервал Δs. Він складений із просторових і часових інтервалів:

Звичайно, це інтервал у системі відліку К. Інтервал у системі К':

Користуючись перетвореннями Лоренца, легко довести, що інтервал у будь-якій інерціальній системі відліку однаковий:

Δs =Δs' .

Просторово-часовий інтервал інваріантний відносно перетворень Лоренца.

Але зміст інваріантності інтервалу не вичерпується цим. Зміст набагато глибший. У цій формулі ві­дображене зовсім нове розуміння таких фундаментальних понять, як простір і час.

Простір і час утворюють єдину форму існування матерії.

Не можна окремо розглядати простір і час. Про це образно сказав Мінковський: «Простір сам по собі і час сам по собі зануряться в ріку забуття, а залишиться жити їхній своєрідний союз».

Ґрунтуючись на понятті інтервалу, Мінковський запропонував доволі струнку геометричну інтерпре­тацію просторово-часових змін.

Квадрат модуля звичайного вектора в просторі трьох вимірів дорівнює сумі квадратів трьох його проекцій на осі координат:

За цією аналогією Мінковський запропонував вважати просторово-часовий інтервал також вектором, який має чотири проекції: три просторові – Δх, Δу, Δz і одну часову – iсΔt, де i – уявна одиниця .

Рис. 6.17.

Тоді

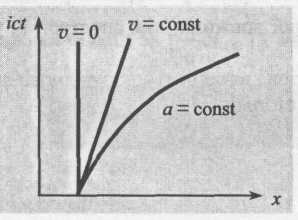
Тобто кожну подію, яка відбувається в даний момент часу в даній точці, слід зображати світовою точкою в чотиривимірному прос­торі. Така точка має три просторові координати й одну часову. Світова точка рухається в цьому чотиривимірному просторі по так званих світових лініях.

На рис.6, як приклад, зображено світові лінії для нерухомої матеріальної точки, для точки, що рухається зі сталою швидкістю, і для точки, що рухається зі сталим прискоренням.