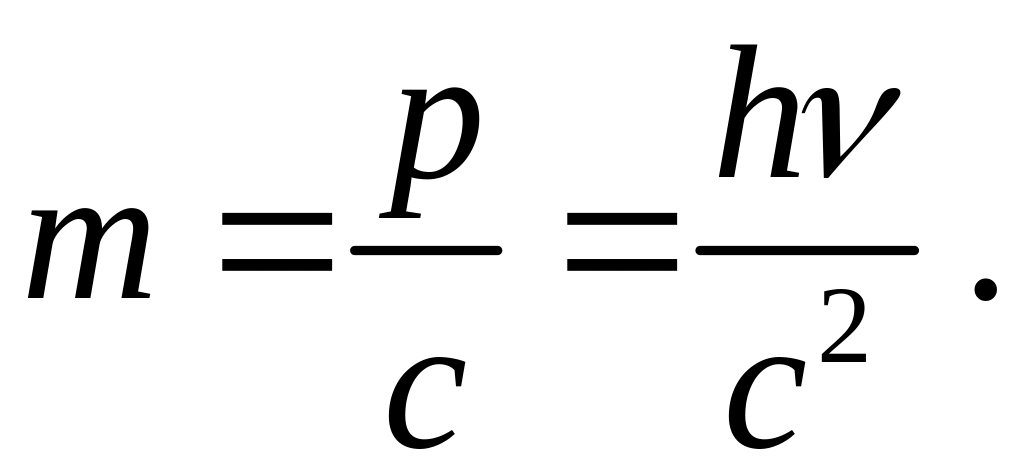Енергія, імпульс і маса фотона.

Фотонами називають найдрібніші частинки світла, або кванти світла. Корпускулярні, або квантові, властивості світла проявляються, наприклад, у явищах фотоефекту або при дослідженні тиску світла. Фотон, як і будь-яка інша матеріальна частинка, має масу, імпульс та енергію.

І все-таки фотон відрізняється від інших частинок тим, що завжди рухається зі сталою швидкістю, яку ніяк не можна змінити.

Швидкість фотона дорівнює швидкості світла, і вона однакова в усих інерціальних системах відліку.

Але тоді з'являються певні утруднення з масою. При υ→с релятивістська маса прямує до нескінченності згідно з формулою

Але цього не може бути! Можна припустити, що маса спокою m₀ дорівнює нулю, і це цілком слушно. Дослід підтверджує, що маса спокою фотона в багато разів менша від маси електрона: m₀<4·10^-21 m_e.

Висновок: частинка з нульовою масою спокою завжди рухається зі швидкістю світла.

Проте маса руху, тобто інертна маса, у фотона є.

Спочатку визначимо інші характеристики фотона: енергію та імпульс. Енергія фотона, як відомо, залежить від частоти електромагнітної хвилі ν:

E=h ν,

де h = 6,63 ·10^-21 Дж · с – стала Планка.

Імпульс фотона знайдемо, скориставшись зв'язком енергії та імпульсу:

Оскільки m₀ = 0, то імпульс фотона

А тепер можна знайти і масу фотона, бо його імпульс p=mc. Маса фотона