Динаміка гармонійного руху. Рух під дією пружних і квазіпружних сил.

а) При прямолінійному гармонійному коливанні прискорення матеріальної крапки змінюється згідно із законом:

(5-9)

;

;

(5-10)

При прямолінійному гармонійному коливанні на матеріальну точку діє сила пропорційна зсуву х і направлена, як і прискорення в сторону, протилежну зсуву ( у бік положення рівноваги ).

Вірне і зворотне твердження.

Силу, що задовольняє умові: вона пропорційна зсуву і направлена вбік протилежно зсуву, називають повертаючою а k – коефіцієнтом повертаючої сили.

б) При крутильних гармонійних коливаннях кутове прискорення:

;

При гармонійних крутильних коливаннях на тіло діє момент сил прямо пропорційний куту повороту і направлений, як і кутове прискорення убік, протилежний повороту (до положення рівноваги). Момент, що задовольняє відміченим умовам, називається повертаючим, а D – коефіцієнтом повертаючого моменту.

(5-10а)

Такими силами, які б змінювалися згідно із законом , є перш за все сили пружності, які виникають в твердих тілах при малих деформаціях розтягування ( стиснення ), а також кручення.

Проте, окрім сил пружності, існують і інші сили підкоряються вказаним законам.

Сили ( моменти сил ), що підкоряються закону ( ), але не є пружними, називаються квазіпружними (майже пружними).

Висновок: Отже, гармонійні коливання матеріальної крапки виникають під дією пружних або квазіпружних сил.

Приклади коливань під дією пружних і квазіпружних сил.

а) пружинний маятник.

Рис. 5.12.

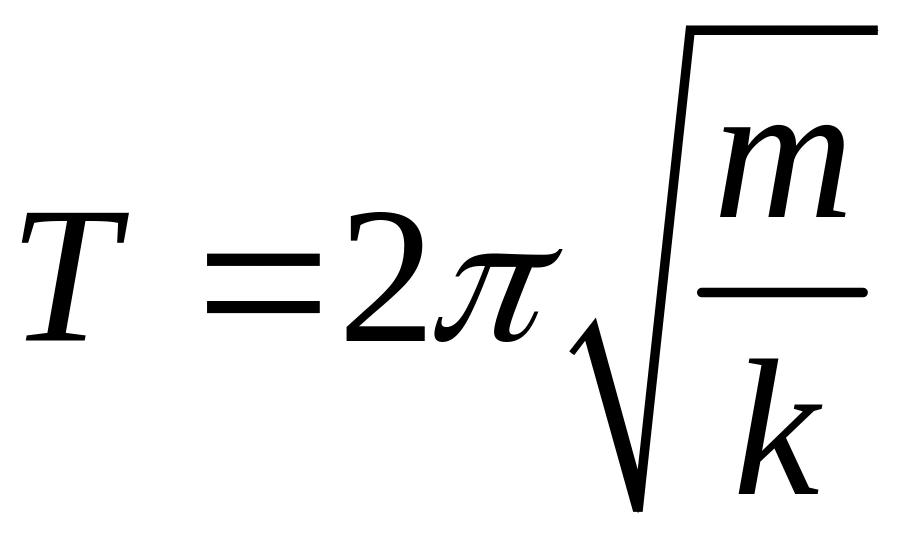
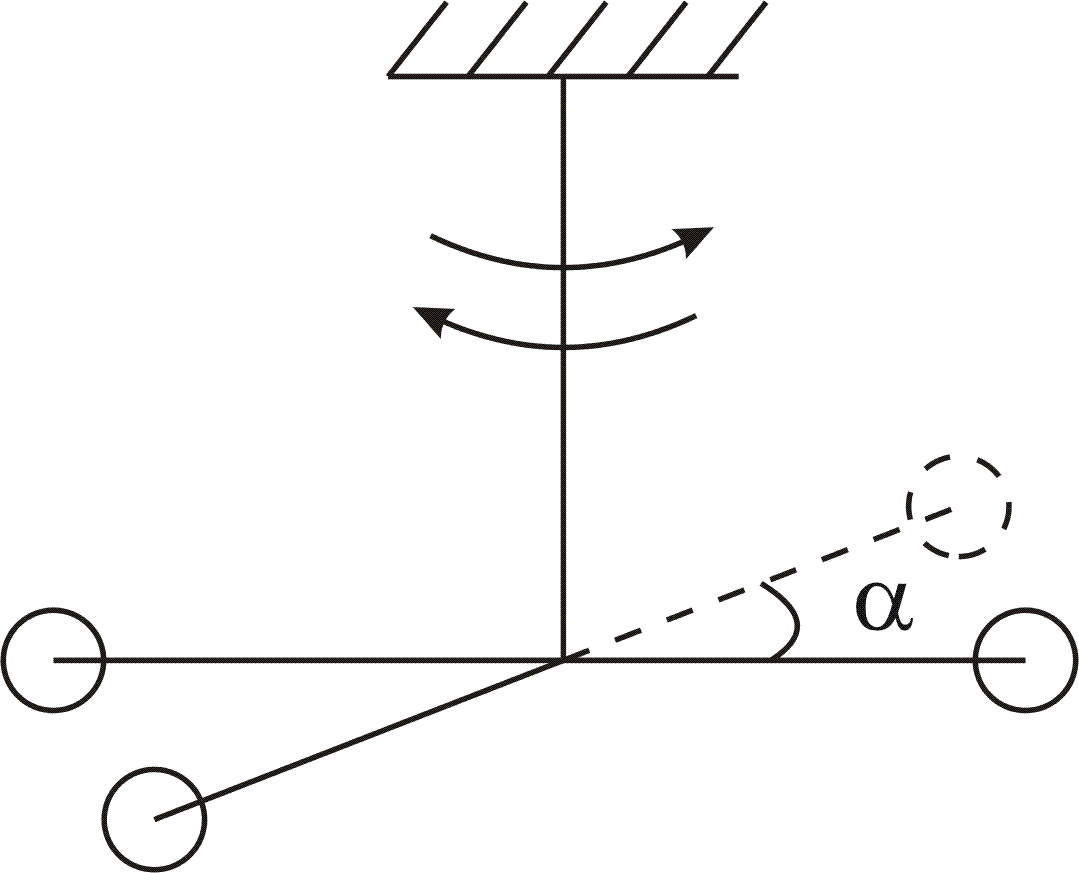
б) крутильний маятник

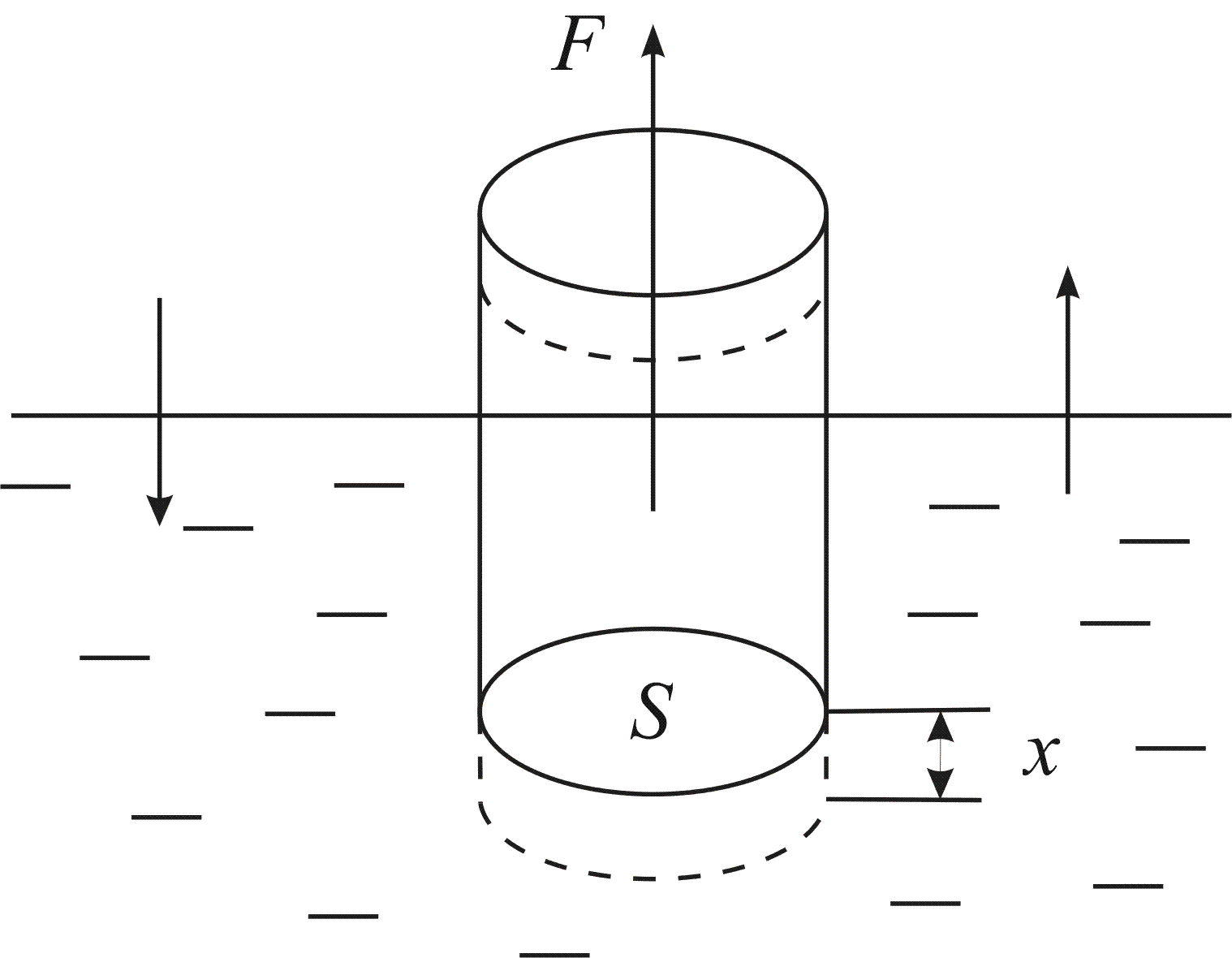
в) коливання плаваючого тіла

Рис. 5.13.

;

Рівняння руху простих механічних коливань систем:

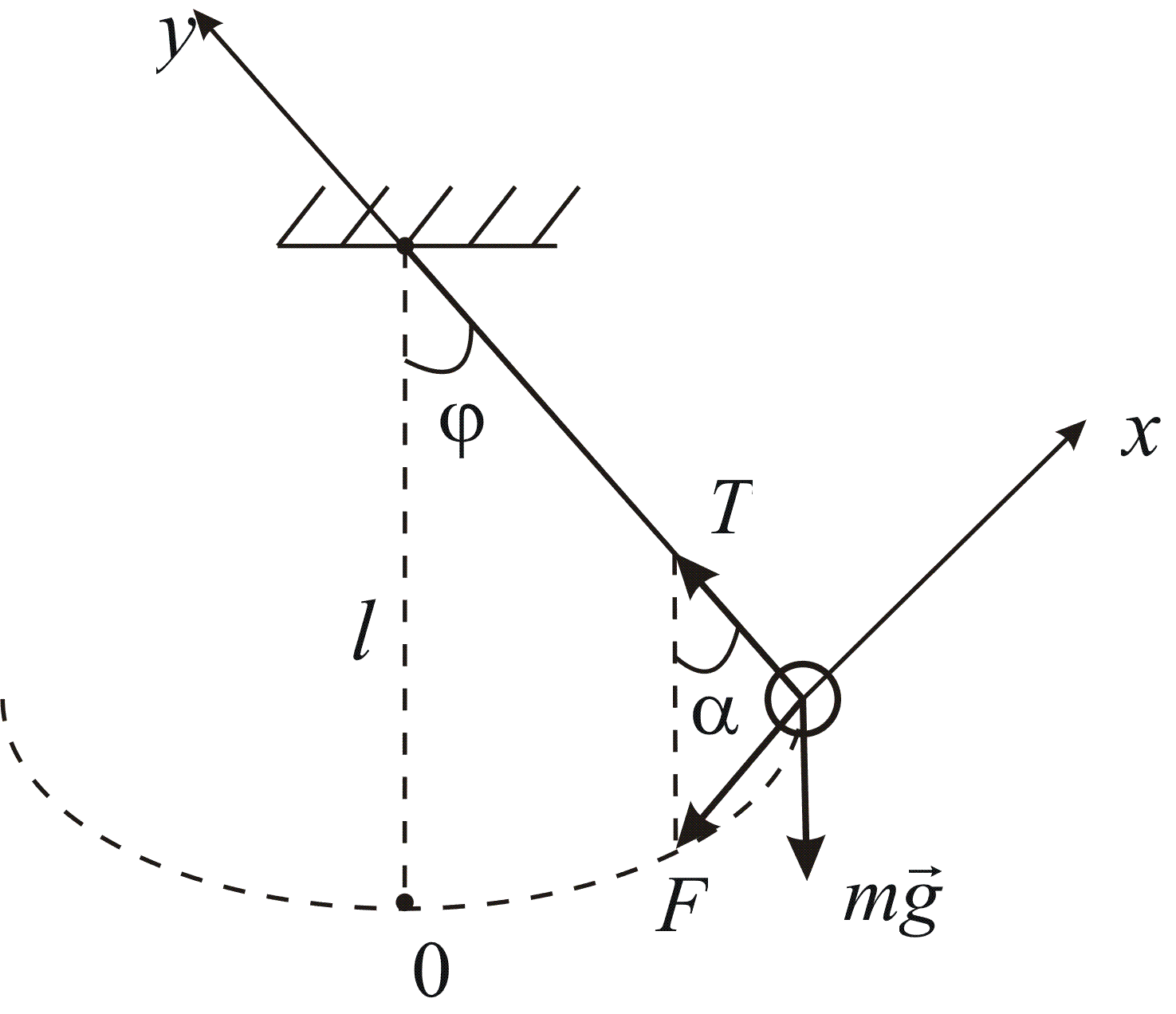
а) Математичний маятник – система, є матеріальною точкою, підвішеною на тонкій невагомій і нерозтяжній нитці.

Рис. 5.14.

;

Таким чином при малих кутах відхилення маятника тангенціальна сила пропорційна відхиленню S і направлена вбік протилежно напряму відхилення. Отже, сила є квазіпружною, а коливання маятника – гармонійними. Порівнюючи k=mω₀²; тоді :

;  (5-10б)

Рішення цього рівняння:

Обертаючий момент:

Динамічне рівняння руху: ; ; ;

; ; ; ;

(5.11)

Якщо точку, що коливається, не можна представити, як матеріальну точку, маятник називається фізичним.

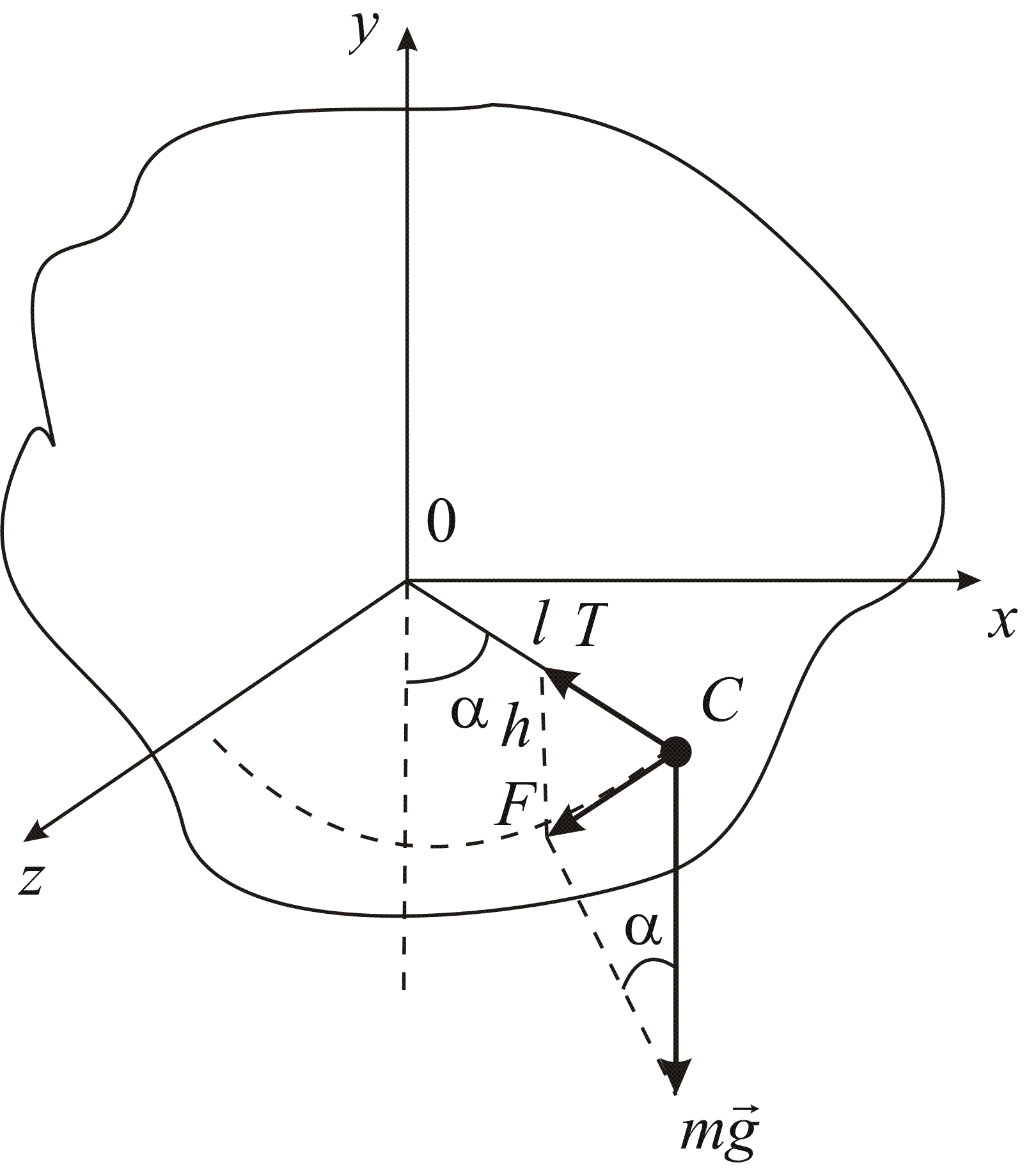
б)Фізичний маятник – тверде тіло, що має нерухому вісь обертання, яка не проходить через його центр тяжіння.

Будучи виведеним з положення рівноваги, тіло скоює біля осі крутильні коливання.

Рис. 5.15.

Обертаючий момент

При малих кутах

I – момент інерції відносно осі обертання.

- приведена довжина фізичного маятника – це довжина такого математичного маятника, який має такий же період коливання, що і даний фізичний маятник.

Обертальний момент:

;

; ; ; ;

(5-12)

; ; (5-13)