Імпульс механічної системи. Рівняння імпульсу механічної системи.

Нехай довільна механічна система складається із n- матеріальних точок з масами m₁, m₂, m₃,….m_i,….m_n.

Тоді імпульс довільної точки:

Імпульсом механічної системи називається сумарний (результуючий) вектор, який дорівнює геометричній сумі векторів імпульсів окремих точок системи.

Нехай на точки системи діють в загальному випадку змінні сили. Розіб’ємо інтервал часу Δt, протягом якого відбувається взаємодія, на нескінченне число нескінченно малих проміжків dt так, що діюча сила .

Тоді застосуємо II закон Ньютона в загальній диференціальній формі, який встановлює взаємозв'язок між імпульсом точки і імпульсом сили, записавши його для кожної ізольованої точки системи: або .

Для точки, що належить механічній системі II закон Ньютона запишеться в диференціальній формі:

,

згідно якого елементарна зміна імпульсу точки механічної системи дорівнює сумі елементарних імпульсів всіх зовнішніх і внутрішніх сил, що діють на точку. Нехай на точки системи діють як внутрішні сили, так і зовнішні:

m₁:

m₂:

.…………………..

m_i:

…………………….

m_n:

Тоді для кожної точки системи II закон Ньютона запишеться:

Щоб знайти загальну (сумарну) зміну імпульсу всіх точок системи необхідно додати почленно всі рівняння руху:

– сумарна елементарна зміна імпульсу всієї механічної системи.

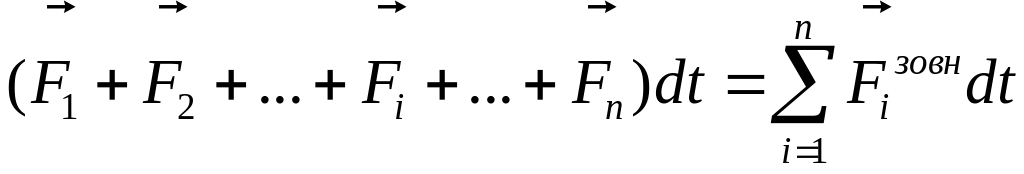– елементарний імпульс результуючої всіх зовнішніх сил.

Якщо додавати імпульси всіх внутрішніх сил, то згідно III закону Ньютона, матимемо:

тоді результуючий вектор внутрішніх сил дорівнює нулю:

і відповідно сумарний імпульс всіх внутрішніх сил теж = 0. Отже маємо:

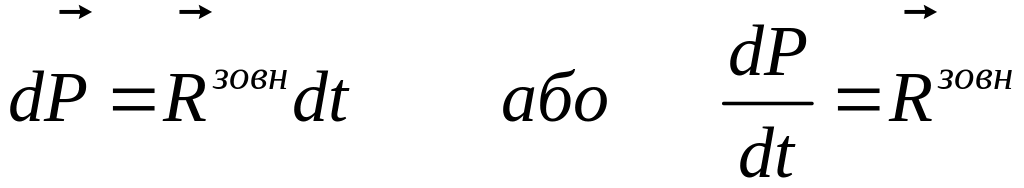(3-19)

Одержаний вираз носить назву рівняння імпульсів механічної системи:

Елементарна зміна імпульсу механічної системи (повний диференціал) дорівнює елементарному імпульсу результуючої всіх зовнішніх сил, що діють на систему;

або: швидкість зміни імпульсу механічної системи дорівнює результуючій всіх зовнішніх сил, що діють на систему.

Закон збереження імпульсу замкненої механічної системи.

Розглянемо випадок замкнутих механічних систем, для яких виконується умова: .

Тоді, використовуючи рівняння імпульсів, маємо:

(3-20)

(3-20а)

Одержаний вираз і складає зміст закону збереження імпульсу замкнутих механічних систем.

Сумарний вектор імпульсу замкнутої механічної системи залишається величиною постійною в процесі її руху, які б зміни не відбувались всередині системи.

Фізична інтерпретація: в процесі взаємодії матеріальної точки (тіла) всередині системи лише обмінюються своїми імпульсами, зберігаючи сумарний імпульс замкнутої механічної системи незмінним. Тобто: внутрішні сили системи не можуть змінити імпульс системи. Зміна імпульсу системи викликається зовнішніми силами. Приклади: легенда барона Мюнхгаузена та ін.