Динамічні характеристики обертального руху.

а) Поняття моменту сили.

Досліди та спостереження показують, що механічний стан рівноваги або стан руху тіла може змінити лише така сила, лінія дії якої не проходить через точку його закріплення або вісь обертання.

Для кількісної оцінки взаємного впливу сили і розміщення її лінії дії відносно осі обертання на зміну механічного стану тіла і вводиться фізична векторна величина – момент сили.

М омент сили – фізична векторна величина, що характеризує обертальну здатність сили і визначається векторним добутком радіус-вектора точки на вектор сили: ;

(3-16)

– плече сили.

Плече сили – найкоротша відстань від осі обертання до лінії дії сили.

(Момент від лат. “movimentum” – рушійна здатність).

З мал. видно, що

Рис. 3.7.

а) Модуль моменту сили дорівнює подвійній площі трикутника побудованого на векторах сили і радіус-вектора.

б) Напрям вектора визначається за правилом векторного добутку: вектор направлений до площини, що визначається векторами і так, що якщо дивитись з кінця його на цю площину, то діюча сила буде намагатись повернути тіло навколо т. О проти годинникової стрілки.

в) Поняття моменту імпульсу точки. У випадку обертального руху матеріальної точки вводиться фізична величина – момент імпульсу, що вважається кількісною мірою обертальної частини руху.

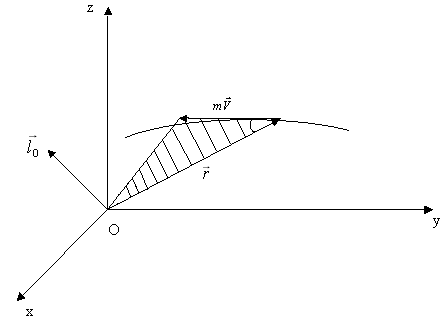
Момент імпульсу матеріальної точки відносно довільного центру визначається векторним добутком радіус-вектора точки на її імпульс:

(3-17)

Рис. 3.8.

Момент імпульсу характеризує не тільки модуль і напрям імпульсу, але і положення точки відносно даного центра О.

Момент імпульсу називається кінетичним моментом точки.

Модуль і напрям визначається аналогічно вектору моменту сили .

, де

Закон збереження моменту імпульсу точки при русі під дією центральної сили.

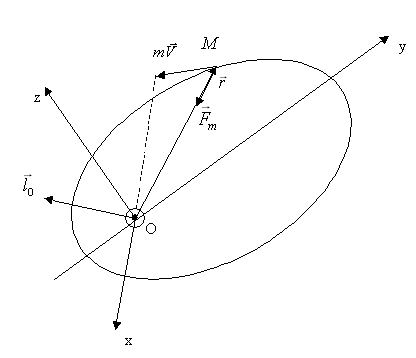
Нехай матеріальна точка рухається під дією сили, лінія дії якої весь час проходить через одну і ту ж нерухому точку О. Така сила називається центральною. Приклади Ц.С.: сила тяжіння (гравітаційна сила), сила пружності – тобто консервативні сили – центральні сили.

Тоді:

Приклад руху точки під дією Ц.С. орбітальний рух Ш.С.З.

Рис. 3.9.

Знайдемо похідну за часом:

, де ;

Так, як – центральна сила, то ; . Тоді:

(3-18)

Момент імпульсу точки, що рухається під дією центральної сили зберігається в процесі її руху.

Динаміка системи матеріальних точок. Закони збереження. Механічні системи та їх класифікація.

Найпростішим матеріальним об’єктом, механічний рух якого досліджується, є матеріальна точка, що є абстракцією реального матеріального тіла. Але в природі, як правило, маємо справу не з окремими тілами (точками), а з системами тіл, точок. Сукупність матеріальних точок (тіл), рух і положення яких взаємозв’язані між собою, називається системою матеріальних точок (тіл), або механічною системою.

Типи механічних систем:

а) консервативні механічні системи, в яких діють потенціальні сили (сили тяжіння і сили пружності);

б) неконсервативні системи, наприклад, в яких діють сили тертя.

Сили, що діють на точки (тіла) системи поділяються на два класи:

а) внутрішні сили – сили, з якими точки (тіла) механічної системи взаємодіють між собою;

б) зовнішні сили – сили, з якими тіла (точки), що не належать до системи, діють на точки (тіла) даної системи.

Остання класифікація – умовна, в залежності від постановки механічної задачі.

Механічні системи, в яких діють тільки внутрішні сили, називаються замкненими (ізольованими). Якщо на механічну систему діють крім внутрішніх і зовнішні сили, то механічна система називається незамкненою. Але в природі замкнених механічних систем не існує (крім Всесвіту в цілому), так як не існує вільних і ізольованих тіл. Іншими словами, замкнена система – абстракція реальних механічних систем.

Математично умову замкнутості механічної системи можна записати:

тобто, система точок називається замкнутою, якщо результуюча всіх зовнішніх сил, що діють на систему, дорівнює нулю.