Фундаментальні взаємодії в природі

До фундаментальних взаємодій належать:

а) гравітаційна;

б) електромагнітна;

в) слабка;

г) сильна, або ядерна;

д) інформаційна.

Гравітаційна взаємодія – взаємодія, що зумовлена взаємним притяганням матеріальних тіл (частинок) одне до одного. Передається через матеріальний посередник – гравітаційне поле. Підкоряється закону всесвітнього тяжіння Ньютона, згідно якого гравітаційна сила зменшується з відстанню по закону оберненого квадрата:

Електромагнітна взаємодія – взаємодія, що виникає між зарядженими тілами (частинками) і передається за допомогою електромагнітного поля. Сили тертя і пружності мають електромагнітну природу. Сюди також належить і вага тіла, яка за природою є силою пружності.

Слабка взаємодія – це взаємодія між окремими елементарними частинками в процесі їх взаємоперетворюваності. Електромагнітна і слабка взаємодія в останній час об’єднані в рамках однієї фізичної теорії.

Сильна взаємодія – взаємодія між елементарними частинками всередині атомного ядра, вона зумовлює ядерні сили, за допомогою яких нуклони об’єднуються в ядра.

Інформаційна взаємодія: У 90-х роках XX сторіччя відкрито нову, п'яту фундаментальну взаємодію – інформаційну, матеріальним посередником якої виявились торсіонні поля, що слугують носієм інформації у тонкому (надтонкому) світі. Тонкий світ - це світ невидимих «не речовинних» явищ і процесів. В науці до понять тонкого світу відносять: поняття свідомості (філософія, психологія), світ нескінченно малих і нескінченно великих величин (математика).

Термін торсіонне походить від англійського слова «torsion», що означає «обертання».

На основі теоретичних та експериментальних досліджень були встановлені три основні властивості торсіонних полів, які істотно відрізняються від відомих фізичних полів: це властивість переносити інформацію без перенесення енергії, передавати інформацію зі швидкістю, яка перевищує швидкість світла, поширюватися не лише в майбутнє, а й у минуле. Ці поля і породжують фізичний вакуум, під яким розуміють в сучасній науці матеріальне середовище, яке народжує і передає взаємодії.

Однією з фундаментальних теоретичних проблем сучасної фізики є створення єдиної фізичної теорії поля, в якій мають бути об’єднані всі фундаментальні взаємодії в природі.

Другий закон динаміки.

З першого закону динаміки випливає, що тіло змінює свій механічний стан спокою або рівномірного прямолінійного руху, тобто набуває прискорення, якщо на нього подіє інше тіло. На запитання, яким буде рух тіла під дією сили, дає відповідь ІІ закон Ньютона, що встановлює кількісний взаємозв’язок між величиною діючої сили, прискоренням і масою тіла.

Цей взаємозв’язок можна встановити за допомогою досліду з візком і капельницею.

Рис. 3.2.

Спочатку встановлюють характер руху візка за допомогою сталої сили. Записуючий пристрій поставить мітки, відстань між якими дорівнює шляхам, пройденим за однаковий проміжок часу Δt. Виявляється, що відношення шляхів, пройдених за проміжки часу Δt, 2Δt, 3Δt …. дорівнює відношенню квадратів цілих чисел 1:2²:3²:…. Ця умова справедлива для рівноприскореного руху:

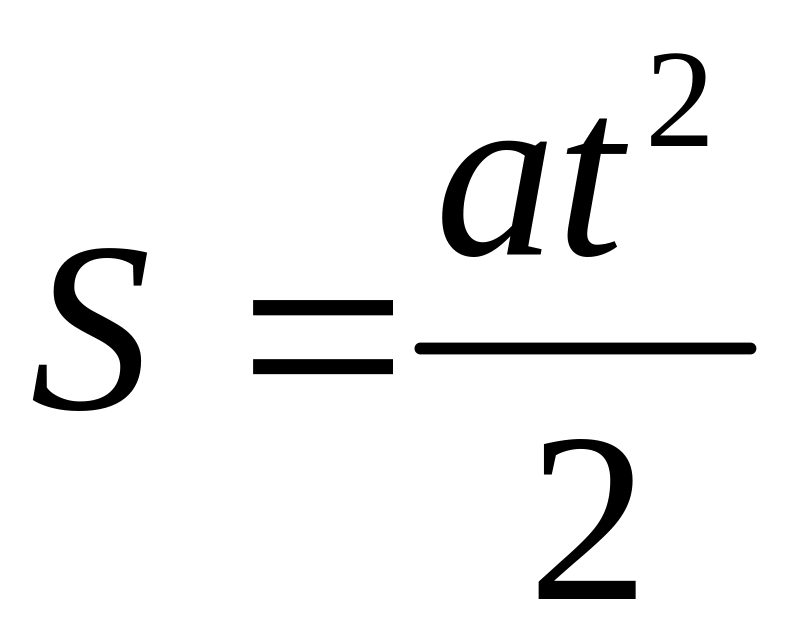
Отже, рух візка під дією сталої сили – рівноприскорений. Далі встановлюють залежність прискорення від величини діючої сили при постійній масі:

а) m=const,

Звідси:

вектори a і F – колінеарні.

б) якщо F=const, а змінювати навантаження візка, тобто його масу, то прискорення при різних навантаженнях буде різним. Причому, із збільшенням навантаження, прискорення, зумовлене дією однією і тією ж силою, зменшується. Отже:

Об’єднуючи обидва результати досліду, маємо:

де a↑↑F, тобто ІІ закон Ньютона носить векторний характер. (3-1)

Висновок. Прискорення, яке отримує тіло під дією прикладеної сили, прямо пропорційне діючій силі, обернено пропорційне масі тіла і направлене в бік діючої сили. Це і є одним із формулювань ІІ закону Ньютона, що виражає функціональну залежність між кінематичними і динамічними величинами.

Перепишемо останній вираз у вигляді:

(3-1а)

Остання формула є математичним записом ІІ закону динаміки, що називається динамічним рівнянням руху, або основного рівняння динаміки матеріальної точки.

Формулювання. В ІСВ сила, що діє на матеріальну точку (тіло), дорівнює добутку маси тіла на прискорення, якого воно набуває.

Принцип незалежної дії сил (принцип суперпозиції) – застосовують, коли на тіло масою m діє декілька сил

Прискорення матеріальної точки при одночасній дії на неї декількох сил дорівнює векторній сумі прискорень, що надають точці окремі сили, тобто вектор прискорення, викликаного дією однієї сили, не залежить від дії інших сил.

(3-1б)

Тоді останній вираз носить назву принцип суперпозиції або незалежні дії сил :

(3-2)

Останній вираз носить назву векторного динамічного рівняння руху. За допомогою цього рівняння розв’язується основна задача механіки, тому воно носить назву основного рівняння динаміки матеріальної точки. Векторне рівняння руху дає три скалярних рівнянь руху:

Скалярна система рівнянь носить назву динамічних рівнянь руху в координатній формі.

(3-2а)

Зауваження:

Із ІІ закону Ньютона випливає, що якщо

Тобто: якщо рівнодійна всіх сил, що діють на тіло, дорівнює нулю, то тіло зберігає стан спокою, або рівномірного прямолінійного руху. Таким чином, І закон Ньютона можна формально розглядати окремим випадком ІІ закону. Незважаючи на це, І закон динаміки має глибоке самостійне значення, а саме: він стверджує існування інерціальних систем відліку, в яких і виконується основний закон динаміки. Цей факт говорить про глибокий взаємозв’язок системи законів динаміки Ньютона.