Коефіцієнт Пуассона

Досліди показують, що деформація лінійного розтягування супроводжується зменшенням поперечного розміру зразка, а деформація стискання – збільшенням поперечного розміру. Зміна поперечних розмірів тіла характеризується коефіцієнтом відносного поперечного стиснення (розтягування).

, де – поперечний розмір тіла до деформації;

– абсолютне значення зміни поперечних розмірів тіла.

Досліди показують, що для всіх тіл з одного й того ж матеріалу відношення коефіцієнта поперечного стиснення (розтягування) до відносної лінійної деформації є величина стала:

.

в честь французького математика і фізика називається коефіцієнтом Пуассона або модулем поперечного стиснення.

~ 0,5 (не перевищує для всіх відомих матеріалів).

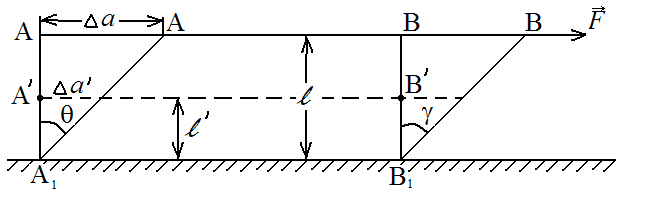
б) деформація зсуву

Рис. 3.11.

Відношення абсолютного зсуву до довжини між рухомими і нерухомими шарами, називається відносним зсувом

абсолютне зміщення (зсув) шару відносно нерухомого шару.

При малих кутах зсуву

Із-за малої деформації абсолютний зсув дорівнює виміряному в радіанах куту зсуву.

При зсуві в середині тіла виникають пружні сили які при статичних деформаціях зрівнюють зовнішню силу, називаються силою зчеплення.

Із-за малої деформації абсолютний зсув прямо пропорційний зовнішній силі зчеплення, довжині границі зміщення від нерухомої сторони та площі рухомого шару.

коефіцієнт зсуву: на практиці – модуль зсуву.

– напруга

При малих деформаціях відносний зсув прямо пропорційний напрузі.

При малих деформаціях пружна напруга прямо пропорційна відносному зсуву.

в) деформація кручення і закон Гука (самостійно)

Границі пружності і міцності.

Рис. 3.12.

Пружна деформація любого виду підкоряється закону Гука, але не для будь-яких напружень. Але закон Гука має місце тільки в деякій мірі: коли деформація лежить нижче деякої границі, яка визначається експериментально.

Пружна деформація любого виду підкоряється закону Гука, але не для будь-яких напружень. Закон Гука має місце тільки в деякій мірі: коли деформація лежить нижче деякої границі, визначається експериментально.

Рис. 3.13.

СД – область пластичної деформації;

ОС – залишкова деформація – деформація, що залишається після дії зовнішніх сил.

ОВ – залишкова деформація;

С – тіло повністю відновлює форму;

ОВ – залишкова деформація розтягування;

ОF – залишкова деформація стиснення;

ОМ – пружна післядія.

Граничне значення напруги, при якому ще не виникають залишкові деформації називаються границею пружності.

Напруга, при якої залишкова деформація досягає величини, тобто деформація збільшується без збільшення навантаження, тобто тіло «тече», називаються границею тягучості. Максимальна напруга, виникає в тілі до руйнування називається границею пружності. В інженерних розрахунках .

Пружна післядія і пружний гістерезис.

Реальні тверді тіла мають слабку залежність: . Ця залежність не міститься у законі Гука.

Досліди показують, що після початку дії зовнішньої сили деформація досягає відповідного значення не відразу а лише по закінченню певного проміжку часу. Після закінчення дії зовнішньої сили деформація зникає також не миттєво, тобто тіло повільно відновлює свою форму і об’єм. Це явище називається пружною післядією.

Для ліквідації залишкової деформації тіло треба стиснути (розтягнути).

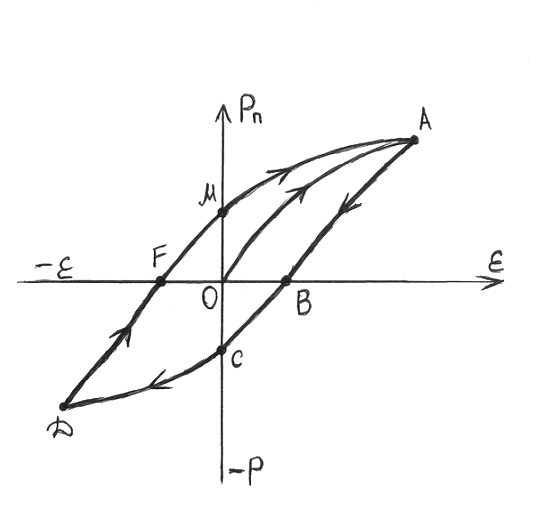
При змінні зовнішньої пружності залежність Р від Е буде виражатися петлею, яка називається петля пружного гістерезису.

Площа петлі гістерезиса пропорційна енергії, що виділяється в тілі (нагрівання) при кожному циклі періодично змінюючої деформації. Чим більша площа петлі гістерезиса, тим більше виділена енергія і тим сильніше нагрівається тіло.

Відповідальні деталі машин виготовляють з металу з вузькою петлею гістерезиса.

Явище пружного гістерезиса полягає у відставанні деформації від зміни прикладеної напруги.