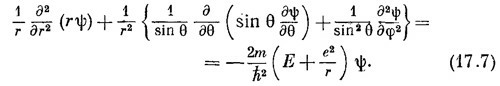- •Дискретный характер испускания и поглощения электромагниного теплового излучения веществом
- •Законы фотоэффекта:
- •Дуализм волновых и корпускулярных свойств излучения
- •Опыты по рассеянию a - частиц
- •Формула Резерфорда
- •Постулаты Бора
- •Границы применяемости квантовой механики
- •Принцип суперпозиции в квантовой механике
- •Частица в одномерной потенциальной яме с бесконечно высокими стенками
- •Квантование энергии электрона в атоме
- •Понятие о вырождении состояний
- •Квантовые числа, их физический смысл
- •Орбитальный, спиновый и полный механический и магнитный моменты электрона.
- •Атом во внешнем магнитном поле
- •Эффект Зеемана
Частица в одномерной потенциальной яме с бесконечно высокими стенками
|
U(x)
= {![]() x < 0, x > L
0
0 < x < L
x < 0, x > L
0
0 < x < L
При таких граничных условиях частица находится внутри потенциальной ямы 0 < x < L и не может выйти за ее пределы, т.е.
![]() (x)
= 0 x < 0, x > L
(x)
= 0 x < 0, x > L
для бесконечной одномерной потенциальной ямы имеем следующее:
Энергия частицы принимает определенные дискретные значения. Обычно говорят, что частица находится в определенных энергетических состояниях.
Частица может находиться в каком-то одном из множества энергетических состояний.
Частица не может иметь энергию равную нулю.
Каждому значению энергии En соответствует собственная волновая функция n, описывающая данное состояние.
Для собственной функции 1(x) вероятность обнаружить частицу в точке x = L/2 максимальна. Для состояния 2(x) вероятность обнаружения частицы в этой точке равна 0.
Квантование энергии электрона в атоме
Некоторые физические величины, относящиеся к микрообъектам, изменяются не непрерывно, а скачкообразно. О величинах, которые могут принимать только дискретные значения, говорят, что они квантуются.
В 1900 г. немецкий физик М. Планк, изучавший тепловое излучение твердых тел, пришел к выводу, что электромагнитное излучение испускается в виде отдельных порций - квантов - энергии. Значение одного кванта энергии равно
ΔE = hν,
где ΔE - энергия кванта, Дж; ν - частота, с-1; h - постоянная Планка (одна из фундаментальных постоянных природы), равная 6,626·10−34 Дж·с. Кванты энергии впоследствии назвали фотонами.
Идея
о квантовании энергии позволила объяснить
происхождение линейчатых атомных
спектров, состоящих из набора линий,
объединенных в серии.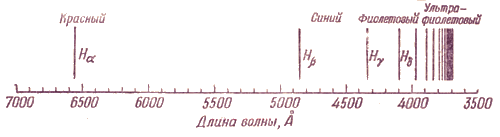
Энергетический спектр (закон дисперсии) — зависимость энергии частицы от импульса. Для свободной частицы закон дисперсии зависит квадратично от импульса. Параболический закон дисперсии встречается в физике твёрдого тела, поскольку при движении электрона в кристалле низкоэнергетический предел имеет параболическую зависимость от квазиимпульса, и по аналогии со свободной частицей вводят эффективную массу для частиц в твёрдом теле, отличную от массы частицы в вакууме. Энергетический спектр в твёрдом теле имеет более сложную структуру по сравнению со свободной частицей. Его знание очень важно для предсказания транспортных, оптических свойств электронного и дырочного газа в полупроводниках. На двумерной гексагональной решётке закон дисперсии линеен по волновому вектору, что делает квазичастицы безмассовыми
Понятие о вырождении состояний
Энергетический уровень квантовой системы называется вырожденным, если содержит более одного состояния. Говоря математически, соответствующее значение энергии является кратным собственным значением гамильтониана.
Количество независимых таких состояний (то есть кратность собственного значения) называется кратностью вырождения.
(Квантовое состояние — любое возможное состояние, в котором может находиться квантовая система.)
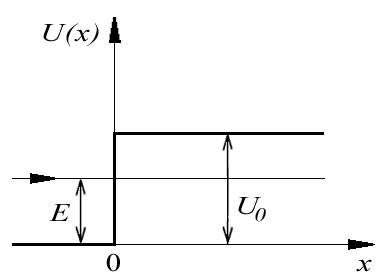
Движение
частицы в области потенциального порога.
Рассмотрим движение частицы в силовом
поле, в котором ее потенциальная
энергия ![]() имеет
вид
имеет
вид
![]()

В
этом случае говорят, что частица находится
в области потенциального порога. На
границе порога, т.е при![]() ,
потенциальная энергия частицы скачком
меняется на конечную величину
,
потенциальная энергия частицы скачком
меняется на конечную величину ![]() (рис.4.7)
.
(рис.4.7)
.
|
Туннельный эффект (туннелирование) — прохождение частицы (или системы) сквозь область пространства, пребывание в которой запрещено классической механикой. Наиболее известный пример такого процесса – прохождение частицы сквозь потенциальный барьер, когда её энергия Е меньше высоты барьера U0.
В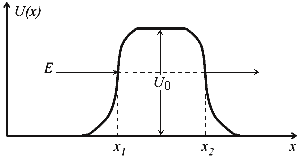 озможность
прохождения частицы сквозь потенциальный
барьер обусловлена требованием
непрерывной волновой функции на стенках
потенциального барьера. Вероятность
обнаружения частицы справа и слева
связаны между собой соотношением,
зависящим от разности E - U(x) в
области потенциального барьера и от
ширины барьера x1 - x2 при
данной энергии.
озможность
прохождения частицы сквозь потенциальный
барьер обусловлена требованием
непрерывной волновой функции на стенках
потенциального барьера. Вероятность
обнаружения частицы справа и слева
связаны между собой соотношением,
зависящим от разности E - U(x) в
области потенциального барьера и от
ширины барьера x1 - x2 при
данной энергии.
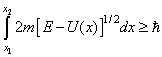
С увеличением высоты и ширины барьера вероятность туннельного эффекта экспоненциально спадает. Вероятность туннельного эффекта также быстро убывает с увеличением массы частицы. Проникновение сквозь барьер носит вероятностный характер. Частица с Е < U0, натолкнувшись на барьер, может либо пройти сквозь него, либо отразиться. Суммарная вероятность этих двух возможностей равна 1. Если на барьер падает поток частиц с Е < U0, то часть этого потока будет просачиваться сквозь барьер, а часть – отражаться.
уравнение Шредингера для линейного гармонического осциллятора
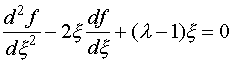
![]() и
и ![]()
При
четных значениях величины ![]() ,
, ![]() это
уравнение есть хорошо известное уравнение
Эрмита, решениями которого
для n=0,1,2... являются
функции
это
уравнение есть хорошо известное уравнение
Эрмита, решениями которого
для n=0,1,2... являются
функции ![]() ,
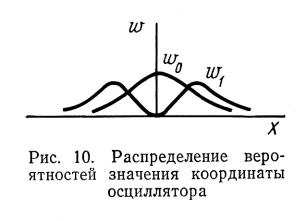
называемыми полиномами Эрмита. Для
низших n полиномы
Эрмита имеют вид:
,
называемыми полиномами Эрмита. Для
низших n полиномы
Эрмита имеют вид:
![]()
![]()
![]()
![]()
.........................................
а для собственных функций и собственных значений гармонического осциллятора мы получим выражения:
![]() (III.30)
(III.30)
![]() (III.31)
(III.31)
Представление физических величин операторами
В квантовой физике существует «нестрогое» правило для построения оператора физических величин: соотношения между операторами в целом такое же, как между соответствующими классическими величинами. Основываясь на этом правиле, были введены следующие операторы (в координатном представлении):
Оператор координат:
![]()
Действие оператора координат заключается в умножении на вектор координат.
Оператор импульса:
![]()
Здесь ![]() — мнимая
единица,
— мнимая
единица, ![]() — оператор
набла.
— оператор
набла.
Оператор кинетической энергии:
![]()
Здесь
— постоянная
Планка, ![]() — оператор
Лапласа.
— оператор
Лапласа.
Оператор потенциальной энергии:
![]()
Действие оператора здесь сводится к умножению на функцию.
Оператор Гамильтона:
![]()
Оператор момента импульса:
![]()
Оператор спина:
В важнейшем случае спина 1/2 оператор спина имеет вид:
![]() ,
где
,
где
![]() ,
, ![]() ,
, ![]() -
т.н. матрицы
Паули.
-
т.н. матрицы
Паули.
Основные свойства собственных
функций. Значения, которые может
принимать данная физическая
величина ![]() называют
в квантовой механике ее собственными
значениями. Нахождение таких значений
тесно связано с математической задачей
определения собственных функций и
соответствующих им собственных значений
оператора
называют
в квантовой механике ее собственными
значениями. Нахождение таких значений
тесно связано с математической задачей
определения собственных функций и
соответствующих им собственных значений
оператора ![]() .
.
Если при действии оператора на некоторую функцию получается та же самая функция, умноженная на число, то есть если
|
то такую функцию
называют собственной функцией оператора
,
а число ![]() его
собственным значением.
его
собственным значением.
Условия возможности одновременного измерения разных механических величин
Если две разные физические
величины ![]() и
и ![]() могут
быть одновременно точно измерены, то
соответствующие им операторы
могут
быть одновременно точно измерены, то
соответствующие им операторы ![]() и
и ![]() должны
быть коммутирующими операторами, то
есть для них должно выполняться
соотношение
должны
быть коммутирующими операторами, то
есть для них должно выполняться
соотношение
![]()
Соотношение неопределённости Гейзенберга
Если имеется несколько (много) идентичных
копий системы в данном состоянии, то
измеренные значения координаты и
импульса будут подчиняться
определённому распределению
вероятности — это
фундаментальный постулат квантовой
механики. Измеряя величину среднеквадратического
отклонения ![]() координаты
и среднеквадратического отклонения
координаты
и среднеквадратического отклонения ![]() импульса,
мы найдем что:
импульса,
мы найдем что:
![]() ,
,
где — приведённая постоянная Планка.
Уравнение Шредингера для атома водорода
Решение уравнения Шрёдингера для водородного атома использует факт, что кулоновский потенциал является изотропным, то есть не зависит от направления в пространстве, другими словами, обладает сферической симметрией.
Уравнение Шрёдингера запишется следующим образом:
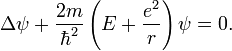
Здесь ψ — волновая
функция электрона в
системе отсчёта протона, m —
масса электрона, ![]() — постоянная
Планка, E — полная
энергия электрона,
— постоянная
Планка, E — полная
энергия электрона, ![]() — оператор
Лапласа. Так как потенциальная
функция зависит от r, а не от
координат по отдельности, удобно будет
записать лапласиан в сферической
системе координат
— оператор
Лапласа. Так как потенциальная
функция зависит от r, а не от
координат по отдельности, удобно будет
записать лапласиан в сферической
системе координат ![]()
В полярных координатах уравнение, которому должна удовлетворять функция ψ(r, θ, φ), принимает вид
|

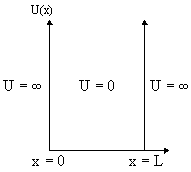 Рис. 1.
Рис. 1.