
- •76 Классическое опр-е вер-ти. Геометрическая вер-ть. Ф-ла полной вер-ти. Ф-ла Байеса.
- •Событие наз. Простым (элементарным), если оно состоит только лишь из одного элементарного исхода, и составным – если k исходов.
- •Геометрическая вероятность
- •77 Повторение испытании. Формула Бернулли. Формула Пуассона. Локальная и интегральная теоремы Муавра и Лапласа.
58 БУЛЕВА АЛГЕБРА И ВОПРОСЫ, СВЯЗАННЫЕ С ЕЕ ПРИМЕНЕНИЕМ
Булева алгебра – непустое мн-во, для кот-го определены три операции: две бинарные операции, представленные знаками , и одна унарная операция, представленная чертой, ставящейся перед эл-том мн-ва(дополнение).
Эл-ты непустого мн-ва(обозн. чер. U) принято обозначать буквами , ,… В результате бинарных операций из произвольных эл-тов и из U получаются более сложные эл-ты: и , кот. соотв-но наз. объединением и пересечением и . По опр-ю для каждого эл-та из мн. U однозначно представлен эл-т -, кот. наз. дополнением к . Для непустого множества U характерно следующее:
вместе с эл-ми и в нем содержатся их теоретико-множественное пересечение () и их теоретико-множественное объединение ();
если эл-т сод-ся в мн-ве U, то в U содержится и теоретико-множественное дополнение к , т. е. мн-во всех подэл-тов из U, кот. не принадлежат . При этом каждый эл-т имеет только одно доп-е.
Система аксиом, предложенная Сикорским :
законы коммутативности : = , =
законы ассоциативности: (С) = ()С , (С) = ()С
законы поглощения: () = , () =
законы дистрибутивности: (С) = ()(С), (С) = ()(С)
(-) = , (-) = . Из этих аксиом следует, что - и -, где - знак включения.
Элемент - наз. нулевым элементом, или нулем бул. алгебры и обознач. .
Элемент - наз. единичным элементом, или единицей бул. алгебры и обозн. .
При этом считается, что когда бул. алгебра явл. полем подмножеств простр.-ва Х, нулевым элементом U явл. пустое множество, а единичным элементом – все пространство Х.
В бул алгебре действительны законы идемпотентности, согласно кот.
= , = .
Бул. алгебра наз. вырожденной алгеброй, если в ней имеется только один эл-т. Необходимым и достаточным усл-ем вырожденности бул. алгебры счит-ся рав.-во =, т.е. совпадение нуля и единицы.
Принятая в бул. алгебре система аксиом основана на принципе двойственности. Запас выводимых в ней формул остается без изменений, если всюду соот-но заменить на , а на .
В булевой логике действительны законы де Моргана, согласно кот.
-( ) = - -, -( ) = - - . Из этих законов следует, что тогда и т. т., когда - -, а также то, что = - (- -), = - (- -).
Когда для непустого подмн.-ва счит.-ся выполненными след. два условия:
из того, что , , следует, что ,
из того, что и , следует, что ,то такое непустое мн.-во наз. идеалом и обознач. гр. бук. ( дельта).
В том случае, когда для непустого подмн.-ва оказ.-ся выполненными след. условия:
из , , следует, что ,
из и , следует, что , то такое непуст. подмн.-во наз фильтром и обозн. переверн. гр. бук. . Понятие фильтра двойственно к понятию идеала.
Если непустое подмн.-во U0 бул. алгебры U замкнуто относительно операций , ,-, т.е. удовлетворяет след. усл.:
если , U0 , то U0
если , U0, то U0
если U0, то - U0, то оно U0 наз. подалгеброй алгебры U.
Отображение (обозн. его ) алгебры U в алгебру U наз. гомоморфизмом, если оно сохраняет операции объединения, пересеч.-я, взятия дополнения, т.е.
( )= () (),( )= () (),(- )= - ().
Взаимно однозначный гомоморфизм наз. изоморфизмом.
Б ул.
алгебра U
наз. атомной,
если для каждого эл.-та
(U)
существует атом а
.
Безатомной бул. алгебра наз. тогда, когда
она не содержит ни одного атома. Атомом
бул. алгебры наз. эл.-т а,
если для любого U
включение а
означает, что или =,
или =
а. Понятие
атома явл. бул. аналогией одноточечного
мн.-ва. Изоморфизм
бул. алгебры U
на себя наз. автоморфизмом.
ул.
алгебра U
наз. атомной,
если для каждого эл.-та
(U)
существует атом а
.
Безатомной бул. алгебра наз. тогда, когда
она не содержит ни одного атома. Атомом
бул. алгебры наз. эл.-т а,
если для любого U
включение а
означает, что или =,
или =
а. Понятие
атома явл. бул. аналогией одноточечного
мн.-ва. Изоморфизм
бул. алгебры U
на себя наз. автоморфизмом.
Самым важным применением теории бул. алгебр считается ее применение к мат. логике. Булев метод позволяет проще и легче доказывать многие фундаментальные теоремы исчисления предикатов, как , напр., теорему о существовании моделей. Булевы алгебры находят широкое применение также в неклассической логике, в теории меры, в функц. анализе, к основаниям теории вероятностей.
Определения:
Бинарная операция – такая операция мат. логики, когда связ.-ся два высказыв.-я в новое, более сложное высказывания.(конъюнкция, дизъюнкция, импликация, эквив.-ть)
Унарная операция – так. операция, в кот. участвует одна пропорциональная связка и одно высказывание. Такими операциями явл.: операция отрицания или , операция необходимости , операция возможности .
Пустое множество – мн.-во, не имеющее эл.-тов (обознач. ) - явл. подмн.-вом любого мн.-ва. В операциях с пустыми мн.-вами действуют след. правила:
М = М М = \ М= М \ = М.
Непустое мн.-во – такое мн.-во, кот имеет хотя бы один элемент.(обозн. М ).
76 Классическое опр-е вер-ти. Геометрическая вер-ть. Ф-ла полной вер-ти. Ф-ла Байеса.
Некоторые определения.
Эксперимент (опыт) – комплекс условий которые могут воспроизводится неограниченное число раз.
Пространством
элементарных исходов
![]() (омега)
наз-ся множество, содержащее все возможные
результаты данного случайного
эксперимента, из которых в эксперименте
происходит ровно один. Элементы этого
множества называют элементарными
исходами
и обозначают
(омега)
наз-ся множество, содержащее все возможные
результаты данного случайного
эксперимента, из которых в эксперименте
происходит ровно один. Элементы этого
множества называют элементарными
исходами
и обозначают
![]() (омега)
с индексами или без.
(омега)
с индексами или без.
Событиями
называют
подмножества множества
,
причем
не обязательно все подмножества множества
,
а лишь множества из некоторого набора
подмножеств. Говорят, что в результате
эксперимента произошло
событие
![]() ,
если
в эксперименте произошел один из
элементарных исходов, входящих в
множество А.
,
если
в эксперименте произошел один из
элементарных исходов, входящих в
множество А.
Вероятностью
события наз. численная
мера степени объективной возможности
события P(A).
Вероятность
события лежит в пределах
![]() .
.
Достоверным наз. событие, которое обязательно происходит в результате эксперимента, то есть единственное событие, включающее все без исключения элементарные исходы – событие .
Невозможным наз. событие, которое не может произойти в результате эксперимента, то есть событие, не содержащее ни одного элементарного исхода («пустое множество» ). Заметим, что всегда .
Событие наз. Простым (элементарным), если оно состоит только лишь из одного элементарного исхода, и составным – если k исходов.
Несколько
событий
![]() образуют
полную группу,
если в результате стохастического (не
можем предугадать результат) эксперимента
произойдет хотя бы одно из них, т.е. их
сумма есть достоверное событие.
образуют
полную группу,
если в результате стохастического (не
можем предугадать результат) эксперимента
произойдет хотя бы одно из них, т.е. их
сумма есть достоверное событие.
Два события наз. несовместными, если в результате опыта появление одного из событии исключает появление другого, т.е. эти события не могут произойти одновременно.
Несколько
событий
наз.
равновозможными,
если
![]() .
.
Условной
вероятностью P(A\B)
события А при наличии события В наз.
вероятность события А, вычисленного
при условии, что событие В произошло:![]() .
.
Классическое определение вероятности Колмагорова
Предположим,
что мы имеем дело с пространством
элементарных
исходов, состоящим из конечного числа
n
элементов:
![]() Более того, предположим, что из каких-
либо соображений мы можем считать
элементарные исходы равновозможными.
Тогда вероятность любого из них
принимается равной 1/n.
Более того, предположим, что из каких-
либо соображений мы можем считать
элементарные исходы равновозможными.
Тогда вероятность любого из них
принимается равной 1/n.
Эти соображения чаще всего не имеют отношения к математической модели и основаны на какой-либо симметрии в эксперименте (симметричная монета, правильная кость). Либо мы можем заранее считать исходы экс-та равновозможными, но тогда рано или поздно возникнет вопрос о соответствии такой мат. модели реальному эксперименту.
Если
событие
![]() состоит
из m
элементарных исходов, то вероятность
этого события равняется
состоит
из m
элементарных исходов, то вероятность
этого события равняется
![]()
Определение.
Говорят, что
эксперимент удовлетворяет классическому
определению вероятности
(или классической вероятностной схеме),
если пространство элементарных исходов
состоит из конечного числа
![]() равновозможных исходов.
равновозможных исходов.
В этом случае вероятность любого события А равна отношению числа исходов, благоприятствующих событию А, к общему числу исходов.
Геометрическая вероятность
Классическое определение вероятности пригодно только для экспериментов с ограниченным числом равномерных элементарных событий.

Рассмотрим
какую-нибудь непрерывную квадрируемую
область
в![]() ,
(на прямой, на плоскости, в пространстве).
Предположим, что «мера»
(длина, площадь, объём, соответственно)
конечна. Пусть случайный эксперимент
состоит в том, что мы наудачу бросаем в
эту область точку
,
(на прямой, на плоскости, в пространстве).
Предположим, что «мера»
(длина, площадь, объём, соответственно)
конечна. Пусть случайный эксперимент
состоит в том, что мы наудачу бросаем в
эту область точку
![]() .
Термин «наудачу»
здесь означает, что вероятность попадания
в любую часть
не
зависит от формы или расположения A
внутри
,
а зависит лишь от «меры» области.
.
Термин «наудачу»
здесь означает, что вероятность попадания
в любую часть
не
зависит от формы или расположения A
внутри
,
а зависит лишь от «меры» области.
Определение.
Эксперимент
удовлетворяет условиям «геометрического
определения вероятности», если его
исходы можно изобразить точками некоторой
области
в
![]() так, что вероятность попадания точки в
так, что вероятность попадания точки в
![]() не зависит от формы или расположения A
внутри
,
а зависит лишь от «меры» области A
( и следовательно, пропорциональна этой
мере):
не зависит от формы или расположения A
внутри
,
а зависит лишь от «меры» области A
( и следовательно, пропорциональна этой
мере):
![]() ,
где
,
где
![]() обозначает
меру обл. A.
обозначает
меру обл. A.
«Мерой» мы пока будем называть длину, площадь, объём.
Если для точки, брошенной в область , выполнены условия геометрического определения вероятности, то говорят, что точка равномерно распределена в области .
Замечание. Если даже эксперимент удовлетворяет геометрическому определению вероятности, далеко не для всех множеств вероятность может быть вычислена как отношение меры А к мере . Причиной этого является существование так называемых «неизмеримых» множеств, то есть множеств, мера которых не существует. А если для всех подмножеств мы можем определить их вероятности, следует сузить класс множеств, называемых «событиями», оставив в этом классе только те множества, для которых мы можем определить вероятность.
Формула полной вероятности.
Пусть событие А может наступить только при условии появления одного из несовместных событий Hi (гипотез), которые образуют полную группу. Тогда вероятность любого события А может быть вычислена по формуле:
![]() .
.
События H1, H2,…, образующие полную группу событий, часто наз. гипотезами. При подходящем выборе гипотез для произвольного события А могут быть сравнительно просто вычислены P(A\Hi) (вероятность событию А произойти при выполнении Hi).
Формула Байеса.
Пусть H1, H2,…- полная группа событий и А- некоторое событие положительной вероятности. Тогда условная вероятность того, что имело место событие Hk, если в результате эксперимента наблюдалось событие А, может быть вычислена по формуле:
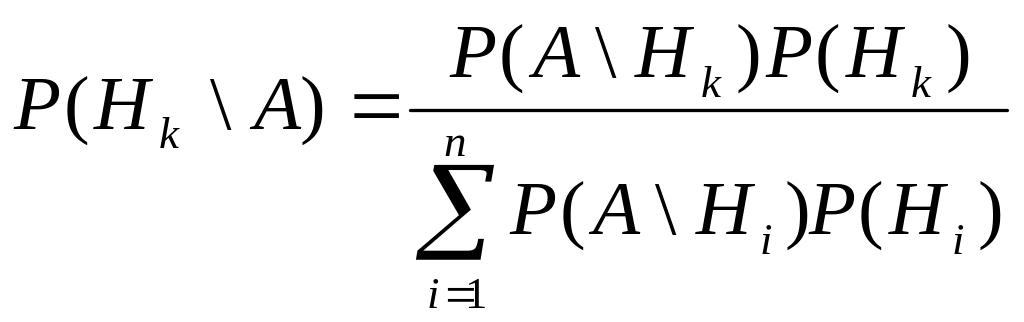 .
.
Формулы Байеса позволяют переоценивать вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.
