Задача № 5

Плотность вероятности случайной величины имеет вид:

Найти: а) параметр ;

б) математическое ожидание и дисперсию случайной величины ;

в) функцию распределения и построить её график.

Оценить с помощью неравенства Чебышева вероятность того, что случайная величина принимает значения на промежутке . Вычислить эту вероятность с помощью функции распределения. Объяснить различие результатов.

Решение.

1. Сначала определим параметр . Для этого воспользуемся основным свойством плотности распределения вероятностей : .

.

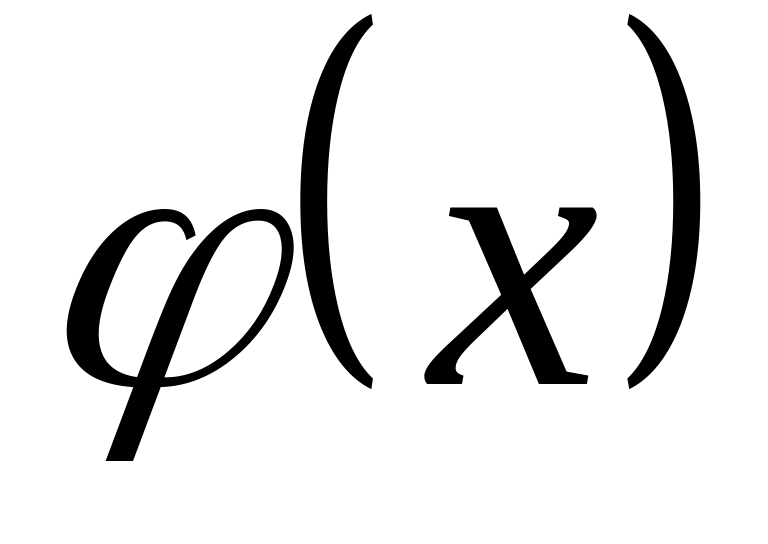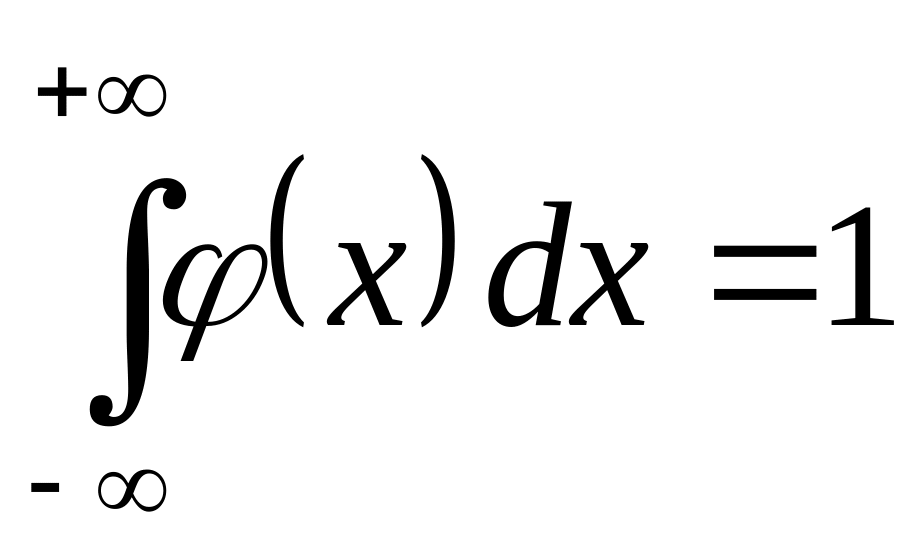, откуда ; .

Значит плотность распределения вероятностей случайной величины задаётся функцией

2. Математическое ожидание

.

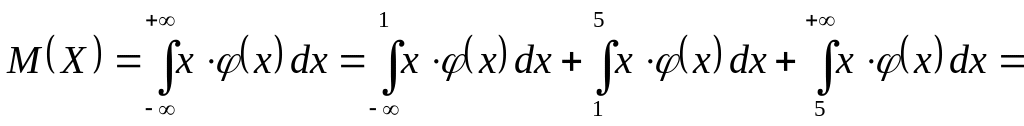
Дисперсия .

.

Значит .

3. Найдём функцию распределения 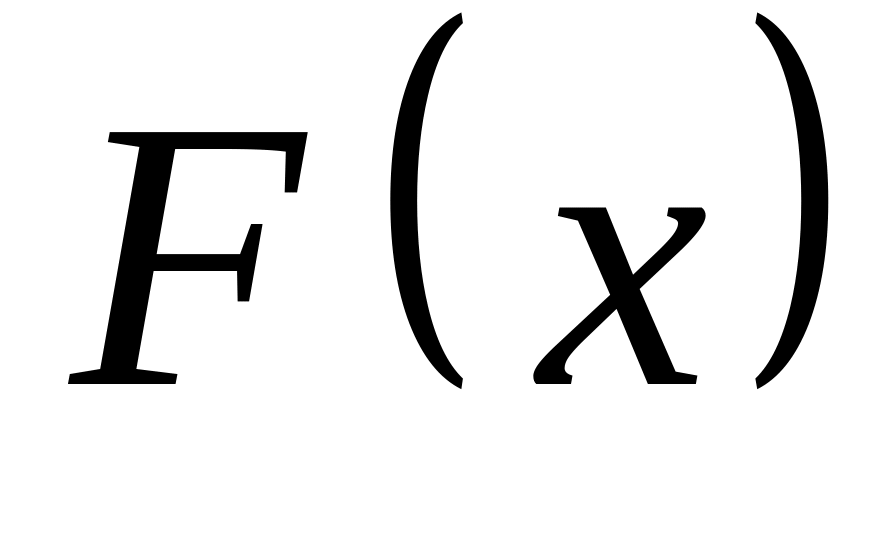случайной величины . Для этого воспользуемся формулой 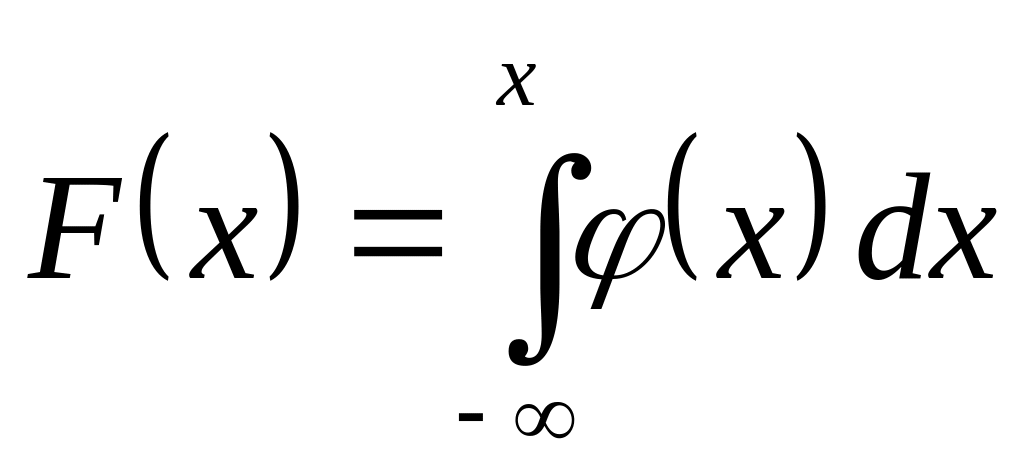, связывающей функцию распределения вероятностей с плотностью распределения вероятностей .

Для и .

Для

.

Для

.

Следовательно, функция распределения случайной величины имеет вид

Схематично построим график функции :

						3
						2
						1
		-2		-1		О		1		2		3		4		5		6		7		Х
						-1
						-2