Лабораторные работы 7_8 / LAB78

1. Постановка задачи.

Требуется, используя квадратурные формулы прямоугольников, трапеций и Симпсона, вычислить значения заданного интеграла и, применив правило Рунге, найти наименьшее значение (наибольшее значение шага ), при котором каждая из указанных формул дает приближенное значение интеграла с погрешностью , не превышающей заданную.

2. Выполнение лабораторной работы.

2. 1. Теоретические сведения.

Повышения точности численного интегрирования добиваются путем применения составных формул. Для этого при нахождении определенного интеграла отрезок разбивают на четное число отрезков длины и на каждом из отрезков длины применяют соответствующую формулу. Таким образом получают составные формулы прямоугольников, трапеций и Симпсона.

На сетке , , , составные формулы имеют следующий вид:

формула прямоугольников

;

формула трапеций

;

формула Симпсона

,

где - остаточные члены. При приближенные значения интегралов для всех трех формул (в предположении отсутствия погрешностей округления) стремятся к точному значению интеграла.

Для практической оценки погрешности квадратурной можно использовать правило Рунге. Для этого проводят вычисления на сетках с шагом и , получают приближенные значения интеграла и и за окончательные значения интеграла принимают величины:

- для формулы прямоугольников;

- для формулы трапеций;

- для формулы Симпсона.

За погрешность приближенного значения интеграла для формул прямоугольников и трапеций тогда принимают величину , а для формулы Симпсона .

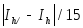2. 2. Интеграл, значение которого требуется вычислить.

2. 3. Текст программы.

# include <math.h>

# include <iostream.h>

double F(double);

double Rectangle(double h, double a, int n)

{

int i;

double y=0,x_i=0;

for (i=0; i<=n-1;i++)

{

x_i=a+i*h;

y=y+h*F(x_i+h/2);

}

return y;

}

double Trapezium(double h, double a, int n)

{

int i;

double y=0,x_i=0,x_i_1=0;

for (i=0; i<=n-1; i++)

{

x_i=a+i*h;

x_i_1=a+(i+1)*h;

y=y+(h/2)*(F(x_i)+F(x_i_1));

}

return y;

}

double Simpson(double h, double a, int m)

{

int i;

double y=0, x_2i=0, x_2i_1=0, x_2i_2=0;

for (i=0; i<=m-1; i++)

{

x_2i=a+2*i*h;

x_2i_1=a+(2*i+1)*h;

x_2i_2=a+(2*i+2)*h;

y=y+(h/3)*(F(x_2i)+4*F(x_2i_1)+F(x_2i_2));

}

return y;

}

double F (double x)

{

return exp(sin(x));

}

void main (void)

{

csr(0);

double h,b,a,eps[3]={0.01,0.001,0.0001},y_R,y_R_1,y_T, y_T_1,y_S, y_S_1;

int m,n,N,n1;

do {

cout<<"\nВведите четное количество интервалов: ";

cin>>N;

n1=fmod(N,2);

if(n1==1)

{cout<<"Неправильный ввод.\nНажмите любую клавишу для повторного ввода.";

waitpress();csr(0);}

} while (n1!=0);

m=N/2;

a=0;//нижий предел

b=1;//верхний предел

for(int i=0;i<3;i++)

{

csr(0);

cout<<"Значение EPS: "<<eps[i]<<endl;

n=N;

do

{

h=(b-a)/n;

y_R=Rectangle(h,a,n);

n=n*2;

h=(b-a)/n;

y_R_1=Rectangle(h,a,n);

}while (fabs(y_R-y_R_1)>eps[i]);

double y,y1;

y1=fabs(y_R_1-y_R);

y=y_R_1+y1/3;

cout<<"\n Значение интеграла (прямоуг.)";

cout<<y;

cout<<"\n Окончательное количество интервалов "<<n<<"\n\n";

n=N;

do{

h=(b-a)/n;

y_T=Trapezium(h,a,n);

n=n*2;

h=(b-a)/n;

y_T_1=Trapezium(h,a,n);

}while (fabs(y_T-y_T_1)>eps[i]);

y1=fabs(y_T_1-y_T);

y=y_T_1-y1/3;

cout<<"\n Значение интеграла (трапеция) "<<y;

cout<<"\n Окончательное количество интервалов "<<n<<"\n\n";

n=N;

do{

h=(b-a)/n;

m=n/2;

y_S=Simpson(h,a,m);

n=n*2;

h=(b-a)/n;

m=n/2;

y_S_1=Simpson(h,a,m);

}while (fabs(y_S-y_S_1)>eps[i]);

y1=fabs(y_S_1-y_S);

y=y_S_1-y1/15;

cout<<"\n Значение интеграла (Симпсон)"<<y;

cout<<"\n Окончательное количество интервалов "<<n<<"\n\n";

waitpress();

}

}

2. 4. Вычисленное значение интеграла.

Результат вычисления интеграла в пакете MathCad 1.631869.

2. 5. Сравнительная характеристика формул.

	Прямоугольников	Трапеций	Симпсона
0.01	Интеграл: 1.63 Интервалов: 4	Интеграл: 1.63 Интервалов: 4	Интеграл: 1.63 Интервалов: 4
0.001	Интеграл: 1.631 Интервалов: 8	Интеграл: 1.631 Интервалов: 16	Интеграл: 1.631 Интервалов: 8
0.0001	Интеграл: 1.6318 Интервалов: 32	Интеграл: 1.6318 Интервалов: 32	Интеграл: 1.6318 Интервалов: 8

Вывод: анализ таблицы показывает, что наиболее точные результаты при малом объёме вычислений даёт формула Симпсона.

1. Постановка задачи.

В лабораторной работе требуется, используя квадратурную формулу Гаусса наивысшего порядка точности, вычислить приближенное значение заданного интеграла.

Интеграл предлагается вычислить по квадратурной формуле Гаусса с восемью узлами:

, ;

,;

,;

,

2. Выполнение лабораторной работы.

2. 1. Теоретические сведения.

В квадратурной формуле Гаусса

узлы и коэффициенты подобраны так, чтобы формула была точна для всех многочленов степени . Для приближенного вычисления интеграла по конечному отрезку выполняется замена переменной ; тогда квадратурная формула Гаусса принимает вид:

,

где ; - узлы квадратурной формулы Гаусса; - гауссовы коэффициенты .

Если подынтегральная функция достаточно гладкая, то формула Гаусса обеспечивает очень высокую точность при небольшом числе узлов.

2. 2. Интеграл, значение которого требуется вычислить.

2. 3. Текст программы.

# include <math.h>

# include <iostream.h>

double F(double x);

double X[8]={-0.96028986,-0.79666648,-0.52553242,-0.18343464,

0.18343464, 0.52553242, 0.79666648, 0.96028986};

double A[8]={0.10122854,0.22238103,0.31370664,0.36268378,

0.36268378,0.31370664,0.22238103,0.10122854};

double Gauss(double a, double b, int n)

{

int i;

double ti,y=0;

for (i=1; i<=n; i++)

{

ti=((a+b)/2)+(b-a)*X[i-1]/2;

y=y+((b-a)/2)*A[i-1]*F(ti);

}

return y;

}

double F (double t)

{

return (1/(log(1+t)));

}

void main (void)

{

double a,b;

a=1;

b=3;

int n=8;

csr(0);

cout<<"\n Значение интеграла: "<<Gauss(a,b,n);

waitpress();

}

2. 4. Вычисленное значение интеграла.

Значение интеграла, вычисленное по формуле Гаусса, равно 1.922421.

Выводы.

Как видно функция между верхним и нижним пределами интегрирования имеет довольно гладкий вид, поэтому метод с использованием функции Гауссса сходится хорошо. Значение интеграла, вычисленное в программе полностью совподает со значением полученным в пакете MathCad.