Cанкт-Петербургский Государственный Электротехнический Университет

КАФЕДРА МОЭВМ

Отчет по курсовой работе

Преподаватель : Титов М. С.

Студент : Евдокимов С. Н.

Санкт-Петербург

Задание на курсовую работу :

Используя программы - функции BISECT , NEWTON , HORDA , ITER, Round из файла metods.cpp найти корень уравнения f(x)=0 с заданной точностью методом бисекции , Ньютона , хорд и итераций соответственно .

Исследуйте обусловленность методов и зависимость числа итераций от точности результата Eps при изменении Eps от 0.1 до 0.000001 .

Порядок выполнения работы :

1. Графически или аналитически отделить корень уравнения f(x)=0 (т.е. найти отрезки [Left, Right], на которых функция f(x) удовлетворяет условиям применимости методов).

2. Составить подпрограмму- функцию вычисления функции f(x) и ее производной f’(x) (при необходимости), предусмотрев округление их значений с заданной точностью Delta с использованием библиотечной функции Round.

3. Составить головную программу, содержащую ввод исходных данных, обращение к подпрограммам BISECT, NEWTON, HORDA, ITER вывод результатов.

4. Выполнить вычисления по программе. Построить графики зависимости числа итераций, необходимых для достижения заданной точности Eps, от величины Eps, а также достижимой точности результатов от точности Delta задания функции f(x) .

5. Теоретически и экспериментально сравнить методы бисекции, Ньютона, хорд и итераций по скорости сходимости и степени обусловленности.

6. Результаты оформить в виде отчета, содержащего постановку задачи, тексты разработанных программ, результаты теоретического и экспериментального анализа в виде таблиц и графиков, выводы.

Теоретическое введение :

В данной работе исследуются четыре метода нахождения корня нелинейного уравнения.

1. Метод Бисекции основан на половинном делении отрезка, на концах которого функция принимает значения разных знаков. Это самый медленный метод из данных, однако он самый точный.

2. Метод Ньютона геометрически эквивалентен замене небольшой дуги кривой y=f(x) касательной, проведенной в некоторой точке кривой. Это один из самых быстрых методов т.к. обладает квадратичной скоростью сходимости. По точности уступает методу Бисекции.

3. Метод Хорд основан на пропорциональном делении отрезка.Это почти самый быстрый метод, однако по точности он уступает методу Бисекции.

4. Метод Простых Итераций основан на замене данной функции другой функцией. Это один из быстрых методов, причем чем ближе к единице взят параметр q, тем бистрее получается результат.

F(x)=x²-5sin(x)

Содержание работы :

1. Локализуем корни уравнения. В данном уравнении два кореня,возьмем больший. Выбераем отрезок, на котором функция, первая () и вторая (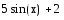) производные монотонны ( см. графики ) , это необходимые условия методов нахождения корня. В данном случае выберем отрезок [1.2;3.2] при корне уравнения » 2.08.

2. Для метода простых итераций вводим новую функцию j(x)=x-a*f(x) 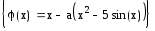Проверяем выполнимость условия монотонности 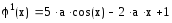(cм. график) . По графику видно, что f’(x)>0 на исследуемом отрезке, следовательно .

   f’(x): 0<m=f₁’(1.2)£f’(x)£f₂’(3.2)=M ; m=0.58821, M=11.3914, q»0.948363, a=0.091325. Выбираем начальное приближение равное левой границе (1.2).

3. Для метода Ньютона выбираем начальное приближение, отвечающее условию f(x₀)*f”( x₀)>0, по графикам видно, что правая граница удовлетворяет этому условию, поэтому в качестве начального приближения берем правую границу, равную 3.2 .

4. Исследуем данные методы по скорости сходимости , изменяя Eps от 0.1 до 0.000001 при Delta =0. Данные и результаты приведены в таблице и отображены на графиках.

5. Исследуем данные методы по степени обусловленности , изменяя Delta от 0.1 до 0.000001 при значениях Eps=0.000001 и Eps=0.01. Данные и результаты приведены в таблице и отображены на графиках.

6. Вычисляем обусловленности f(x) =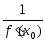= 0,151579 è j(x)==1.65972