Рассуждения с нечеткими множествами

В формальной логике по отношению к множествам действует два предположения, которые не могут нарушаться:

1. Установление принадлежности (любой элемент является либо членом множества, либо членом дополнения этого множества).

Дополнение – это операция, которая ставит в соответствие подмножеству М множества Х другое подмножество N, также принадлежащее Х, так что по этим двум подмножествам множество Х может быть восстановлено.

2. Закон исключения третьего (элемент не может одновременно принадлежать и множеству и его дополнению).

Оба эти положения нарушаются в так называемой теории нечетких множеств (fuzzy set theory) автора Лофти Заде (Zadeh). Именно он множества и законы традиционной логики назвал четкими, а свои множества – нечеткими.

Главное утверждение Заде относится к 1983 г. и говорит о том, что теория вероятностей является хорошим инструментом для измерения количества случайной информации, но не подходит для измерения смысла информации.

Пример:

Путаница, которая возникает при распознавании слов и фраз естественного языка связанна не с неопределенностью этих слов с точки зрения их случайности, а с отсутствием ясности, как их распознать.

Именно это играет важнейшую роль для определения меры достоверности правил, по которым определяется вывод. Для измерения такой неопределенности, связанной со смыслом, Заде разработал теорию возможностей.

В ней сформулировано два основных положения:

1. количественное выражение точности, для чего введена функция принадлежности, которая принимает значения в интервале от 0 до 1;

2. понятие нечеткого множества (fuzzy set)

Пусть S – некоторое множество, а – его элемент.

Нечеткое подмножество F этого множества S определяется функцией принадлежности mF( ), которой задают степень принадлежности элемента подмножеству F.

Рассмотрим пример:

Пусть S – множество всех положительных чисел. И пусть мы хотим задать множество малых целых чисел. Это будет нечеткое подмножество F.

Функцию принадлежности для него можно задать, например, в таком виде:

В общем случае для описания принадлежности некоторого элемента множеству F необходимо задать такую функцию принадлежности mF для всего множества элементов S, которому F принадлежит как подмножество.

Создание таких конкретных функций для разных задач – это первый важный вопрос теории нечетких множеств.

Второй вопрос этой теории – это создание таких отношений, таких правил вычисления комбинированных возможностей, которые позволяют производить вычисления на выражениях, содержащих нечеткие переменные.

Заде ввел правила для вычисления меры возможности для операций логических «или» (or) и логических «и» (and) над такими выражениями.

Эти правила напоминают соответствующие выражения стэндфордской алгебры фактора уверенности. А именно, если две предпосылки правила связанны логическим «или», то в качестве меры берется максимум, если же логической «и», то – минимум.

Рассмотрим классический пример задачи управления из теории нечетких множеств.

Пусть в вертикальном положении необходимо удерживать перевернутый маятник за счет передвижения его основания.

В искусственных системах классический подход к решению такой задачи состоит в измерении Q отклонения маятника от вертикали, скорости отклонения dQ/dt и формировании закона управления перемещением основания на базе решения системы дифференциальных уравнений. Это очень сложная задача при таком традиционном подходе. Решение есть, но в очень ограниченном диапазоне малых углов отклонения Q.

Теория нечетких множеств дает эффективный алгоритм управления в реальном времени без этих ограничений и позволяет построить контроллер , входными сигналами для которого являются отклонение Q и скорость dQ/dt, а выходными сигналами – детерминированный неразмытый закон управления.

Обычно этот сигнал формируется в виде величины и направления перемещения основания системы.

Внутри контроллера входные данные интерпретируются как два нечетких подмножества Q и dQ/dt, которые затем используются в множестве нечетких правил.

Этот второй шаг реализуется с помощью нечеткой ассоциативной матрицы (fuzzy associative matrix). В этой матрице входы и выходы контроллера кодируются напрямую.

Правила не объединяются в цепочку, как при традиционном решении. Все применимые на данном шаге правила активизируются и срабатывают, а затем их результаты объединяются. При этом общий результат задается, также как и входные параметры, областью пространства нечетких выходных параметров.

И, наконец, эта область подвергается операции, которая называется дефазификацией для получения четкого управляющего воздействия.

Таким образом, и выходы здесь четкие, т.е. внешне контроллер ведет себя как обычное устройство управления, а внутри между этими двумя точками действуют законы нечетких множеств.

Упростим задачу: пусть движение происходит в плоскости, а именно:

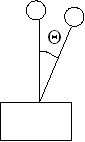
Вправо положительное отклонение, влево - отрицательное. Соответственно положительным или отрицательным может быть и перемещение основания.

Измеряются угол Q и скорость dQ/dt. Вырабатывается управляющее воздействие U.

Рассмотрим конкретный пример.

Пусть необходимо удерживать в вертикальном положении маятник на плоскости. Измеряются угол отклонения маятника Q вправо или влево и скорость этого отклонения dQ/dt. Необходимо сформировать перемещение основания маятника вправо или влево с тем, чтобы удержать маятник в вертикальном положении.

Пусть отклонение Q меняется в пределах -2 2 радиан, а скорость может колебаться в пределах -5 5 °/с.

На первом шаге необходимо представить эти входные сигналы в виде размытых множеств с соответствующими функциями принадлежности.

Пусть каждый из входных сигналов может находиться в одной из трех областей:

• области N отрицательных значений;

• области P положительных значений;

• области Z нулевых значений.

Для Q функция принадлежности в этом случае может иметь вид:

-2 -1 0 1 2

Аналогично для угловой скорости функция принадлежности имеет вид:

Общие правила задания этих функций принадлежности:

1. Область равновесия находится в области нулевых значений. Задается эта область так: ордината равна единице в нулевой точке (точке равновесия) и из этой точки значения функций принадлежности линейно падают до границ изменения сигнала.

2. Области положительных и отрицательных значений в точке равновесия начинаются из нуля и линейно нарастают до границ изменения входного сигнала, становясь на границе равными единице, и для значений вне диапазона остаются равными единице.

На следующем, втором шаге, необходимо задать формируемый выходной сигнал в виде размытого множества.

Пусть сигнал управления перемещением основания маятника меняется в интервале -24 24 единиц. В рассматриваемом случае целесообразно ввести пять областей неоднозначности для выходного сигнала, что зависит от того, совпадает ли характер областей у обоих входных сигналов. Эта функция принадлежности имеет вид:

Здесь уже пять областей неоднозначности выходного сигнала:

Z – область нулевых значений;

N – область отрицательных значений;

NB – область больших отрицательных значений;

PB – область больших положительных значений;

Попадание выходного сигнала в ту или иную область при соответствующих значениях входных сигналов напрямую кодируется с помощью ассоциативной матрицы, которая в данном случае имеет вид:

dQ\dt Q	P	Z	N
P	PB	P	Z
Z	P	Z	N
N	Z	N	NB

Введем обозначения: Q ; dQ/dt .

Этой ассоциативной матрице в базе знаний с учетом введенных обозначений будут соответствовать следующие правила:

if =P and =P then U=PB

if =P and =Z then U=P

if =Z and =P then U=P

if =Z and =Z then U=Z

if =Z and =N then U=N

if =N and =Z then U=N

if =N and =P then U=Z

if =P and =N then U=Z

if =N and =N then U=NB

Теперь для каждого из результатов этих правил необходимо определить в соответствии с правилами Заде значения функции принадлежности.

Рассмотрим этот шаг на примере:

Пусть перемещение Q=1, а скорость dQ/dt=-4. В соответствии с их функциями принадлежности Q=1 принадлежит двум областям: нулевой области Z и положительной области P, причем каждой из них со значениями функции равной 0,5. Значение скорости, равное –4, также принадлежит двум областям: области отрицательных значений N и области нулевых значений Z. Но функция принадлежности для области Z равна 0,2, а для области N – 0,8.

Итак, может принадлежать области Z и P, а – областям N и Z. Это означает, что из девяти записанных правил в данном случае будут активизированы 4, в которых и принимают соответствующие значения.

Активизируются 4 правила, в которых предпосылки связанны логическими «и». Поэтому в соответствии с сформулированными правилами определяются функции принадлежности результата для каждого из этих правил будет браться минимальное из значений функции принадлежности предпосылок.

if =P and =Z then U=P

min(0.5, 0.2)=0.2P

if =P and =N then U=Z

min(0.5, 0.8)=0.5Z

if =Z and =Z then U=Z

min(0.5, 0.2)=0.2Z

if =Z and =N then U=N

min(0.5, 0.8)=0.5N

Итак, в соответствии с теорией Заде сработало не одно, а все правила, которые включают входные сигналы в соответствующих областях.

Теперь необходимо объединить эти результаты.

Для этого выбираются все области, в которых может находиться выходной сигнал. В них строится фигура, ограниченная границами самих областей и соответствующими уровнями функции принадлежности.

И на последнем шаге определяется координата центра тяжести этой фигуры.

Этот метод объединения результатов наиболее распространен и называется методом центра тяжести.

Выполним этот шаг для рассматриваемого примера.

Выходной сигнал может находиться в трех областях N, Z, P. Причем в соответствии со срабатывающими правилами функция принадлежности принимает следующие значения:

1. 0.2P;

2. 0.5Z;

3. 0.2Z;

4. 0.5N.

Здесь два правила, которые приводят к попаданию в одну и ту же область. Такой результат требует объединения. Так как правила независимы, а результаты объединены логическим «или», тогда в соответствии с сформулированными правилами из этих двух результатов нужно взять максимум:

Строим ограниченную границами областей и уровнями функций принадлежности фигуру.

Осталось определить центр тяжести.

Центр тяжести этой фигуры соответствует значению U=-2.

Итак, на контроллер здесь поступили реальные измеряемые неразмытые сигналы Q=1 и dQ/dt=-4. В результате контроллер выработал обычный управляющий сигнал величиной две единицы в отрицательном направлении.

Это управляющее воздействие применяется в системе, опять измеряются Q и dQ/dt, цикл повторяется, а маятник удерживается в вертикальном положении.

Таким образом, аппарат Заде дает инженеру мощный инструментарий для решения задач управления в тех случаях, когда традиционный аппарат с оптимальным управлением не справляется.