
Министерство образования и науки РФ
Санкт-Петербургский государственный электротехнический университет
“ЛЭТИ”
кафедра МОЭВМ
Лабораторная работа №5 по дисциплине вычислительная математика
на тему:
«Метод Ньютона».
г. Санкт-Петербург
-
Год
I. Цель работы:
Найти корень уравнения
![]() для функции
для функции
![]() методом Ньютона с заданной точностью
Eps, исследовать скорость
сходимости и обусловленности метода.
методом Ньютона с заданной точностью
Eps, исследовать скорость
сходимости и обусловленности метода.
II. Общие сведения:
В
случае, когда известно хорошее начальное
приближение решения уравнения
![]() ,
эффективным методом повышения точности
является метод Ньютона. Он состоит в
построении итерационной последовательности
,
эффективным методом повышения точности
является метод Ньютона. Он состоит в
построении итерационной последовательности
![]() сходящейся к корню уравнения
сходящейся к корню уравнения
![]() .
.
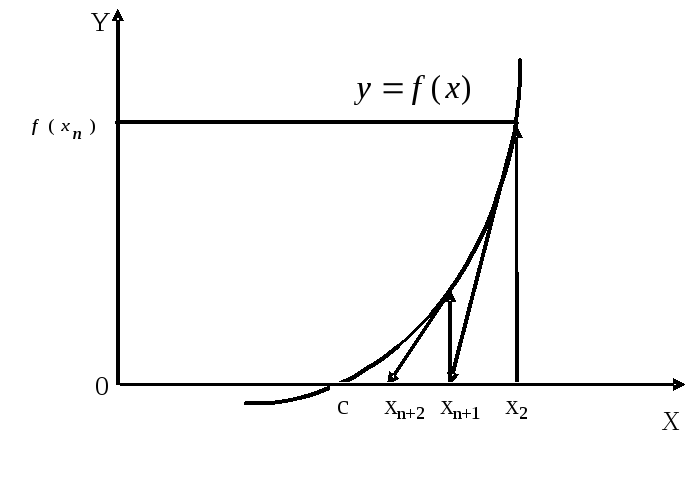
Метод
Ньютона допускает простую геометрическую
интерпретацию (рис. 2). Если через точку
с координатами
![]() провести касательную, то абсцисса точки
пересечения этой касательной с осью Ох
будет очередным приближением xn+1
корня
уравнения
провести касательную, то абсцисса точки
пересечения этой касательной с осью Ох
будет очередным приближением xn+1
корня
уравнения
![]() .
.
Для оценки погрешности n-го приближения корня предлагается пользоваться неравенством
![]()
где
М2-наибольшее
значение модуля второй производной
![]() на отрезке [a,b];
m1-наименьшее
значение модуля первой производной
на отрезке [a,b];
m1-наименьшее
значение модуля первой производной
![]() на отрезке [a,b].
Таким образом, если
на отрезке [a,b].
Таким образом, если
![]() то
то
![]() Это означает, что при хорошем начальном
приближении корня после каждой итерации
число верных десятичных знаков в
очередном приближении удваивается,
т.е. процесс сходится очень быстро (имеет
место квадратическая сходимость). Из
указанного следует, что при необходимости
нахождения корня с точностью
итерационный процесс можно прекращать,
когда
Это означает, что при хорошем начальном
приближении корня после каждой итерации
число верных десятичных знаков в
очередном приближении удваивается,
т.е. процесс сходится очень быстро (имеет
место квадратическая сходимость). Из
указанного следует, что при необходимости
нахождения корня с точностью
итерационный процесс можно прекращать,
когда
![]() (3.1)
(3.1)
Рассмотрим
один шаг итераций. Если на (n-1)-м
шаге очередное приближение xn-1
не
удовлетворяет
условию окончания процесса, то вычисляются
величины
![]() и следующие приближение корня
и следующие приближение корня
![]() При выполнении условия (3.1) величина xn
принимается
за приближенное значение корня с,
вычисленное с точностью .
При выполнении условия (3.1) величина xn
принимается
за приближенное значение корня с,
вычисленное с точностью .
III. Порядок выполнения работы:
-
Графически или аналитически отделить корень уравнения
 (т.е. найти отрезки [Left,
Right],
на которых функция
(т.е. найти отрезки [Left,
Right],
на которых функция
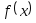 удовлетворяет
условиям сходимости метода Ньютона).
удовлетворяет
условиям сходимости метода Ньютона). -
Составить подпрограмму - функцию вычисления функции
 ,
f’(x)
предусмотрев округление значений
функции с заданной точностью Delta.
,
f’(x)
предусмотрев округление значений
функции с заданной точностью Delta. -
Составить головную программу, вычисляющую корень уравнения
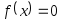 и содержащую обращение к подпрограммам
,
и содержащую обращение к подпрограммам
,
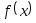 ,
,
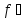 (x),
Round,
NEWTON
и индикацию результатов.
(x),
Round,
NEWTON
и индикацию результатов. -
Выбрать начальное приближение корня x0 из [Left, Right] так, чтобы
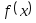
 >0.
>0. -
Провести вычисления по программе. Исследовать скорость сходимости метода и чувствительность метода к ошибкам в исходных данных.
IV. Выполнение работы:
-
Отделим графическим методом корни уравнения
 ,
т.е. найдем отрезки
,
т.е. найдем отрезки
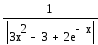
![]() удовлетворяет
условиям применимости метода бисекции.
Для этого сначала определим абсолютное
число обусловленности задачи вычисления
корня:
удовлетворяет
условиям применимости метода бисекции.
Для этого сначала определим абсолютное
число обусловленности задачи вычисления
корня:
 =
,
=
,
тогда Eps ≤ Delta / |1/(3x2-3+2e-x) |.
Теперь графически определим отрезок [Left, Right].

Где
![]() .
.
Проанализировав результаты, мы получаем
отрезок [1, 2]. На этом отрезке мы можем
брать любое начальное приближение x,
т. к.
![]() ∙
∙![]() >0
всюду на отрезке [1, 2].
>0
всюду на отрезке [1, 2].
2)Составим
подпрограмму вычисления функции
![]() и производной этой функции f’(x)
= 3x2
–
3 + 2e(-x).
и производной этой функции f’(x)
= 3x2
–
3 + 2e(-x).
double F(double x)
{
extern double c,d,delta;
double s;
long int S;
s = x*x*x-3*x-2*exp(-x);
if( s/delta < 0 )
S = s/delta - .5;
else
S = s/delta + .5;
s = S*delta;
s = Round( s,delta );
return(s);
}
double F1(double x)
{
extern double delta;
double s;
long int S;
s = 3*x*x-3+2*exp(-x);
if( s/delta < 0 )
S = s/delta - .5;
else
S = s/delta + .5;
s = S*delta;
s = Round( s,delta );
cout<<" {f'(x)="<<s<<"}"<<endl;
return(s);
}
3)Составляем головную программу, вычисляющую корень уравнения с заданной точностью Eps и содержащую обращение к подпрограмме f(x), программам-функциям NEWTON, Round и представление результатов.
void main()
{
clrscr();
int k;
long int s;
float x11,eps1,delta1;
double x1,eps,x;
double F(double);
printf("Input eps: ");
scanf("%f",&eps1);
eps = eps1;
printf("Input x1: ");
scanf("%f",&x11);
x1 = x11;
printf("Input delta: ");
scanf("%f",&delta1);
delta = delta1;
x = NEWTON(x1,eps,k);
printf("x=%f k=%d\n",x,k);
getch();
}
4) Проведем вычисления по программе, варьируя значения параметров Eps (точность вычисления корня) и Delta (точность задания исходных данных).
|
eps |
delta |
a |
b |
x1 |
x* |
k |
f(x*) |
|
|
|
0,000001 |
0,1 |
1 |
2 |
1,5 |
1,792345 |
2 |
0,047736173 |
0,143459 |
|
|
0,00001 |
0,1 |
1 |
2 |
1,5 |
1,792345 |
2 |
0,047736173 |
0,143459 |
|
|
0,0001 |
0,1 |
1 |
2 |
1,5 |
1,792345 |
2 |
0,047736173 |
0,143459 |
|
|
0,001 |
0,1 |
1 |
2 |
1,5 |
1,792345 |
2 |
0,047736173 |
0,143459 |
|
|
0,01 |
0,1 |
1 |
2 |
1,5 |
1,792345 |
2 |
0,047736173 |
0,143459 |
|
|
0,1 |
0,1 |
1 |
2 |
1,5 |
1,792345 |
2 |
0,047736173 |
0,143459 |
|
|
0,000001 |
0,01 |
1 |
2 |
1,5 |
1,785154 |
3 |
-0,002120657 |
0,145014 |
|
|
0,00001 |
0,01 |
1 |
2 |
1,5 |
1,785154 |
3 |
-0,002120657 |
0,145014 |
|
|
0,0001 |
0,01 |
1 |
2 |
1,5 |
1,785154 |
3 |
-0,002120657 |
0,145014 |
|
|
0,001 |
0,01 |
1 |
2 |
1,5 |
1,785154 |
3 |
-0,002120657 |
0,145014 |
|
|
0,01 |
0,01 |
1 |
2 |
1,5 |
1,785154 |
3 |
-0,002120657 |
0,145014 |
|
|
0,1 |
0,01 |
1 |
2 |
1,5 |
1,790901 |
2 |
0,03768143 |
0,143769 |
|
|
0,000001 |
0,001 |
1 |
2 |
1,5 |
1,785470 |
3 |
5,89554E-05 |
0,144945 |
|
|
0,00001 |
0,001 |
1 |
2 |
1,5 |
1,785470 |
3 |
5,89554E-05 |
0,144945 |
|
|
0,0001 |
0,001 |
1 |
2 |
1,5 |
1,785470 |
3 |
5,89554E-05 |
0,144945 |
|
|
0,001 |
0,001 |
1 |
2 |
1,5 |
1,785470 |
3 |
5,89554E-05 |
0,144945 |
|
|
0,01 |
0,001 |
1 |
2 |
1,5 |
1,785470 |
3 |
5,89554E-05 |
0,144945 |
|
|
0,1 |
0,001 |
1 |
2 |
1,5 |
1,790933 |
2 |
0,037904014 |
0,143762 |
|
|
0,000001 |
0,0001 |
1 |
2 |
1,5 |
1,785461 |
4 |
-3,13644E-06 |
0,144947 |
|
|
0,00001 |
0,0001 |
1 |
2 |
1,5 |
1,785461 |
4 |
-3,13644E-06 |
0,144947 |
|
|
0,0001 |
0,0001 |
1 |
2 |
1,5 |
1,785461 |
4 |
-3,13644E-06 |
0,144947 |
|
|
0,001 |
0,0001 |
1 |
2 |
1,5 |
1,785461 |
4 |
-3,13644E-06 |
0,144947 |
|
|
0,01 |
0,0001 |
1 |
2 |
1,5 |
1,785490 |
3 |
0,00019694 |
0,144941 |
|
|
0,1 |
0,0001 |
1 |
2 |
1,5 |
1,790882 |
2 |
0,037549275 |
0,143773 |
|
|
0,000001 |
0,00001 |
1 |
2 |
1,5 |
1,785462 |
4 |
3,76262E-06 |
0,144947 |
|
|
0,00001 |
0,00001 |
1 |
2 |
1,5 |
1,785462 |
4 |
3,76262E-06 |
0,144947 |
|
|
0,0001 |
0,00001 |
1 |
2 |
1,5 |
1,785462 |
4 |
3,76262E-06 |
0,144947 |
|
|
0,001 |
0,00001 |
1 |
2 |
1,5 |
1,785462 |
4 |
3,76262E-06 |
0,144947 |
|
|
0,01 |
0,00001 |
1 |
2 |
1,5 |
1,785483 |
3 |
0,000148645 |
0,144943 |
|
|
0,1 |
0,00001 |
1 |
2 |
1,5 |
1,790886 |
2 |
0,037577097 |
0,143772 |
|
|
0,000001 |
0,000001 |
1 |
2 |
1,5 |
1,785462 |
4 |
3,76262E-06 |
0,144947 |
|
|
0,00001 |
0,000001 |
1 |
2 |
1,5 |
1,785462 |
4 |
3,76262E-06 |
0,144947 |
|
|
0,0001 |
0,000001 |
1 |
2 |
1,5 |
1,785462 |
4 |
3,76262E-06 |
0,144947 |
|
|
0,001 |
0,000001 |
1 |
2 |
1,5 |
1,785462 |
4 |
3,76262E-06 |
0,144947 |
|
|
0,01 |
0,000001 |
1 |
2 |
1,5 |
1,785483 |
3 |
0,000148645 |
0,144943 |
|
|
0,1 |
0,000001 |
1 |
2 |
1,5 |
1,790886 |
2 |
0,037577097 |
0,143772 |
|
eps |
delta |
a |
b |
x1 |
x* |
k |
f(x*) |
|
|
|
0,000001 |
0,1 |
0 |
90 |
86 |
1,785440 |
12 |
-0,000148014 |
0,371503 |
|
|
0,00001 |
0,1 |
0 |
90 |
86 |
1,785440 |
12 |
-0,000148014 |
0,371503 |
|
|
0,0001 |
0,1 |
0 |
90 |
86 |
1,785440 |
12 |
-0,000148014 |
0,371503 |
|
|
0,001 |
0,1 |
0 |
90 |
86 |
1,785440 |
12 |
-0,000148014 |
0,371503 |
|
|
0,01 |
0,1 |
0 |
90 |
86 |
1,785440 |
12 |
-0,000148014 |
0,371503 |
|
|
0,1 |
0,1 |
0 |
90 |
86 |
1,785440 |
12 |
-0,000148014 |
0,371503 |
|
|
0,000001 |
0,01 |
0 |
90 |
86 |
1,786826 |
13 |
0,00942374 |
0,370994 |
|
|
0,00001 |
0,01 |
0 |
90 |
86 |
1,786826 |
13 |
0,00942374 |
0,370994 |
|
|
0,0001 |
0,01 |
0 |
90 |
86 |
1,786826 |
13 |
0,00942374 |
0,370994 |
|
|
0,001 |
0,01 |
0 |
90 |
86 |
1,786826 |
13 |
0,00942374 |
0,370994 |
|
|
0,01 |
0,01 |
0 |
90 |
86 |
1,785826 |
13 |
0,002515709 |
0,371361 |
|
|
0,1 |
0,01 |
0 |
90 |
86 |
1,787271 |
12 |
0,012501153 |
0,370831 |
|
|
0,000001 |
0,001 |
0 |
90 |
86 |
1,785465 |
13 |
2,44599E-05 |
0,371494 |
|
|
0,00001 |
0,001 |
0 |
90 |
86 |
1,785465 |
13 |
2,44599E-05 |
0,371494 |
|
|
0,0001 |
0,001 |
0 |
90 |
86 |
1,785465 |
13 |
2,44599E-05 |
0,371494 |
|
|
0,001 |
0,001 |
0 |
90 |
86 |
1,785465 |
13 |
2,44599E-05 |
0,371494 |
|
|
0,01 |
0,001 |
0 |
90 |
86 |
1,785465 |
13 |
2,44599E-05 |
0,371494 |
|
|
0,1 |
0,001 |
0 |
90 |
86 |
1,786623 |
12 |
0,00802057 |
0,371069 |
|
|
0,000001 |
0,0001 |
0 |
90 |
86 |
72,462218 |
4 |
380265,2739 |
0,004664 |
|
|
0,00001 |
0,0001 |
0 |
90 |
86 |
72,462218 |
4 |
380265,2739 |
0,004664 |
|
|
0,0001 |
0,0001 |
0 |
90 |
86 |
72,462218 |
4 |
380265,2739 |
0,004664 |
|
|
0,001 |
0,0001 |
0 |
90 |
86 |
72,462218 |
4 |
380265,2739 |
0,004664 |
|
|
0,01 |
0,0001 |
0 |
90 |
86 |
72,462218 |
4 |
380265,2739 |
0,004664 |
|
|
0,1 |
0,0001 |
0 |
90 |
86 |
75,762224 |
3 |
434641,4079 |
0,004459 |
|
|
0,000001 |
0,00001 |
0 |
90 |
86 |
84,415770 |
36 |
601295,4058 |
0,003996 |
|
|
0,00001 |
0,00001 |
0 |
90 |
86 |
84,415770 |
36 |
601295,4058 |
0,003996 |
|
|
0,0001 |
0,00001 |
0 |
90 |
86 |
84,415770 |
36 |
601295,4058 |
0,003996 |
|
|
0,001 |
0,00001 |
0 |
90 |
86 |
84,415770 |
35 |
601295,4058 |
0,003996 |
|
|
0,01 |
0,00001 |
0 |
90 |
86 |
84,415770 |
35 |
601295,4058 |
0,003996 |
|
|
0,1 |
0,00001 |
0 |
90 |
86 |
86,222318 |
25 |
640742,8875 |
0,003911 |
|
|
0,000001 |
0,000001 |
0 |
90 |
86 |
25,841938 |
82 |
17179,86922 |
0,013418 |
|
|
0,00001 |
0,000001 |
0 |
90 |
86 |
25,841938 |
82 |
17179,86922 |
0,013418 |
|
|
0,0001 |
0,000001 |
0 |
90 |
86 |
25,841938 |
81 |
17179,86922 |
0,013418 |
|
|
0,001 |
0,000001 |
0 |
90 |
86 |
25,841938 |
81 |
17179,86922 |
0,013418 |
|
|
0,01 |
0,000001 |
0 |
90 |
86 |
25,841938 |
81 |
17179,86922 |
0,013418 |
|
|
0,1 |
0,000001 |
0 |
90 |
86 |
25,822004 |
2 |
17140,0237 |
0,013429 |
Точное значение:
x* = 1,7854615
f(x*) = 0.00000031
5) Из полученных результатов видно, что, чем более высокая точность выходных данных нам необходима, тем больше нам необходимо сделать итераций. Кроме того, из таблицы видно, что с ростом ошибок в исходных данных, уменьшается точность выходных данных. Таким образом, теоретические результаты совпадают с экспериментальными данными.
