Лабораторная работа

Министерство образования РФ

Санкт-Петербургский Государственный Электротехнический Университет

Кафедра ВМ – 2

Индивидуальное задание №3

по дисциплине: «Вычислительная математика»

вариант № 19

Выполнил: студент гр. 2373

Маннанов Б.Г.

Проверил:

Санкт-Петербург 2004 г.

I Прямые итерации для системы Ах = b при х0 = (1,1,1,1,1); t = ¾.

, где D – диагональная матрица, состоящая из диагональных элементов матрицы А:

Расчётная формула:

В результате проведения 20-ти итераций получаем:

II Метод Зайделя для системы Ах = b при х0 = (1,1,1,1,1).

A = A^– + D + A⁺, где А^– и А⁺ – верхнедиагональная и нижнедиагональная подматрицы А.

Формула итераций метода:

Расчётная формула:

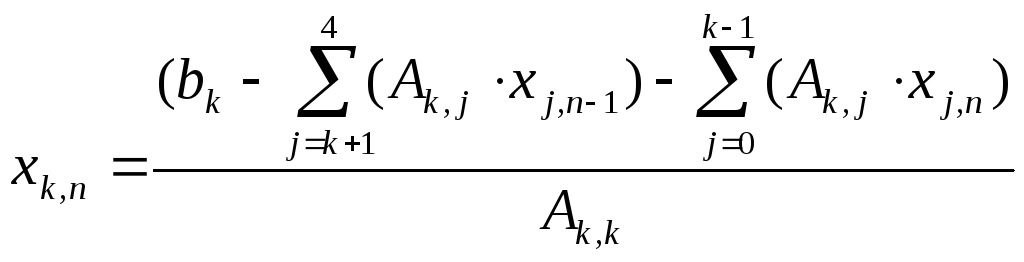
Результаты проведения итераций:

Метод сходится уже после 10-й итерации!

III Метод релаксаций для системы Ах = b при х0 = (1,1,1,1,1); w=4/3.

Формула метода:

Расчётная формула:

Метод даёт следующие результаты:

IV Метод Зайделя для системы (А+ΔA)х = b при х0 = (1,1,1,1,1).

A + ΔA = B

Получаем следующие результаты:

V Метод релаксаций для системы (А+ΔA)х = b при х0 = (1,1,1,1,1); w=4/3.

A + ΔA = B

Получаем следующие результаты:

Не сходится!