3.4. Метод Ньютона

305. В случае, когда известно хорошее начальное приближение решения уравнения , эффективным методом повышения точности является метод Ньютона. Он состоит в построении итерационной последовательностисходящейся к корню уравнения. Достаточные условия сходимости метода сформулированы в[1,7].

306. Метод Ньютона допускает простую геометрическую интерпретацию (рис. 3.2). Если через точку с координатами провести касательную, то координата точки пересечения этой касательной с осью абсцисс будет очередным приближениемx_{n +1} корня уравнения.

307. 

308. Для оценки погрешности n-го приближения корня предлагается пользоваться неравенством

5. 

309. где М₂ - наибольшее значение модуля второй производнойна отрезке(a, b); m₁ - наименьшее значение модуля первой производнойна отрезке(a, b).

310. Таким образом, если тоЭто означает, что при хорошем начальном приближении корня после каждой итерации число верных десятичных знаков в очередном приближении удваивается, т. е. процесс сходится очень быстро (имеет место квадратичная сходимость). Из указанного следует, что, при необходимости нахождения корня с точностьюe, итерационный процесс можно прекращать, когда соблюдается неравенство

6. . (3.1)

311. Рассмотрим один шаг итераций. Если на (n-1)-м шаге очередное приближениеx_{n -1} не удовлетворяет условию окончания процесса, то вычисляются величиныи следующее приближение корня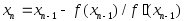. При выполнении условия(3.1)величинаx_n принимается за приближенное значение корняс, вычисленное с точностьюe.

Лабораторная работа № 5

315. В лабораторной работе предлагается, используя подпрограммы-функцииNEWTON иRoundиз файлаmethods.cpp (файл заголовковmethods.h,директорияLIBR1), найти корень уравнения 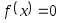с заданной точностьюEpsметодом Ньютона, исследовать скорость сходимости и обусловленность метода.

316. Для данной работы вид функции задается преподавателем индивидуально каждому студенту из числа вариантов, приведенных в 3.6.

317. Порядок выполнения лабораторной работы.

318. 1) Графически или аналитически отделить корень уравнения (т. е. найти отрезки(Left, Right),на которых функция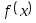удовлетворяет условиям сходимости метода Ньютона).

319. 2) Составить подпрограммы вычисления функций ,, предусмотрев округление их значений с заданной точностьюDelta.

320. 3) Составить головную программу, вычисляющую корень уравнения и содержащую обращения к подпрограммам-функциям, , Round,NEWTONи индикацию результатов.

321. 4) Выбрать начальное приближение корня x₀ из(Left, Right)так, чтобы.

322. 5) Провести вычисления по программе. Исследовать скорость сходимости метода и его чувствительность к ошибкам в исходных данных, сравнить скорости сходимости методов Ньютона, бисекции и хорд.

323. Для приближенного вычисления корней уравнения 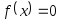методом Ньютона предназначена подпрограмма-функцияNEWTON, текст которой представлен в 3.7.

3.5. Метод простых итераций

325. Метод простых итераций решения уравнения состоит в замене исходного уравнения эквивалентным ему уравнениеми построении последовательности, сходящейся приn ® ¥ к точному решению. Достаточные условия сходимости метода простых итераций формулируются теоремой, приведенной в[1,2,7].

326. Рассмотрим один шаг итерационного процесса. Исходя из найденного на предыдущем шаге значения ,вычисляется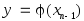.Если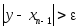, то принимаетсяx_n = y и выполняется очередная итерация. Если же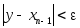, то вычисления заканчиваются и за приближенное значение корня принимается величинаx_n = y. Погрешность результата вычислений зависит от знака производнойприпогрешность определения корня составляет, а припогрешность не превышаетe. Здесьq-число такое, чтона отрезке(a, b).Существование числаqявляется условием сходимости метода в соответствии с названной ранее теоремой.

327. Для применения метода простых итераций определяющее значение имеет выбор функции в уравнении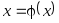, эквивалентном исходному. Функциюнеобходимо подбирать так, чтобы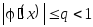. Это обусловливается тем, что еслина отрезке(a, b), то последовательные приближения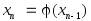будут колебаться около корняc, если же, то последовательные приближения будут сходиться к корнюc монотонно. Следует также помнить, что скорость сходимости последовательности{x_n}к корнюc функциитем выше, чем меньше числоq.