
- •Введение
- •1. Особенности машинной арифметики,точность вычислений на эвм
- •Лабораторная работа № 1
- •2. Изучение понятия обусловленности вычислительной задачи
- •Лабораторная работа № 2
- •3. Решение нелинейных уравнений
- •3.1. Общие сведения
- •3.2. Метод бисекции
- •Лабораторная работа № 3
- •3.3. Метод хорд
- •Лабораторная работа №4
- •3.4. Метод Ньютона
- •Лабораторная работа № 5
- •3.5. Метод простых итераций
- •Лабораторная работа № 6
- •3.6. Курсовая работа по дисциплине и варианты заданий
- •3.7. Программы для решения нелинейных уравнений
- •4.Численное интегрирование
- •4.1. Составные формулы прямоугольников, трапеций, Симпсона
- •Лабораторная работа № 7
- •4.2. Формула Гаусса
- •Лабораторная работа № 8
- •Список литературы
- •197376, С.-Петербург, ул. Проф. Попова, 5
3.1. Общие сведения
Пусть задана непрерывная функция
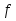 вещественного аргументаxи требуется численным методом решить
уравнение
вещественного аргументаxи требуется численным методом решить
уравнение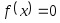 ,
т. е. найти приближениеx*
к вещественному корню этого
уравнения. Если уравнение имеет несколько
вещественных корней, то сначала
производят их отделение (изоляцию), а
затем уточняют положение отдельного
корня. Считается, что отделение корня
произведено, если выделен такой интервал(a0,
b0)
области определения функции
,
т. е. найти приближениеx*
к вещественному корню этого
уравнения. Если уравнение имеет несколько
вещественных корней, то сначала
производят их отделение (изоляцию), а
затем уточняют положение отдельного
корня. Считается, что отделение корня
произведено, если выделен такой интервал(a0,
b0)
области определения функции
 ,
на концах которого значения функции
,
на концах которого значения функции
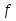 (a0)
и
(a0)
и
 (b0)имеют разные знаки и внутри которого
имеется только один корень уравнения
(b0)имеют разные знаки и внутри которого
имеется только один корень уравнения .
Для уточнения метода используют
итерационные методы, такие как метод
бисекции (половинного деления), метод
хорд (секущих или ложного положения),
метод Ньютона (касательных), метод
итераций (последовательных приближений).
В указанных методах вычисляются либо
последовательность значений границ
сужающихся интерваловa0,
b0,
a1,
b1,
...,
an,
bn,
содержащих корень, либо
последовательность приближений к корнюx0,
x1,
x2,
. . ., xn,
[2,7,8,11].
.
Для уточнения метода используют
итерационные методы, такие как метод
бисекции (половинного деления), метод
хорд (секущих или ложного положения),
метод Ньютона (касательных), метод
итераций (последовательных приближений).
В указанных методах вычисляются либо
последовательность значений границ
сужающихся интерваловa0,
b0,
a1,
b1,
...,
an,
bn,
содержащих корень, либо
последовательность приближений к корнюx0,
x1,
x2,
. . ., xn,
[2,7,8,11].В первом случае итерационный процесс заканчивается, как только длина текущего интервала становится достаточно малой (например,
 ).Во втором случае условием остановки
вычислений является малость очередного
приращенияhn
=xn-xn
-1,
½hn½<e.В
обоих случаях величина параметраeопределяет момент остановки вычислений.
Иногда в качестве критерия остановки
используют условие½
).Во втором случае условием остановки
вычислений является малость очередного
приращенияhn
=xn-xn
-1,
½hn½<e.В
обоих случаях величина параметраeопределяет момент остановки вычислений.
Иногда в качестве критерия остановки
используют условие½ (
( )½<e, где
)½<e, где
 -
текущее приближение к корню, например,
-
текущее приближение к корню, например,
 =1/2
(an
+
bn
)
в методе бисекции. Выполнение этого
условия свидетельствует о малости
значения функции в точке
=1/2
(an
+
bn
)
в методе бисекции. Выполнение этого
условия свидетельствует о малости
значения функции в точке
 ,
т. е. позволяет считать, что
,
т. е. позволяет считать, что
 .
.Для каждого итерационного метода можно указать некоторые условия сходимости. Однако не всегда легко проверить или гарантировать выполнение этих условий. Кроме того,необходимо учесть особенности машинных вычислений при реализации итерационных методов. На практике эти затруднения обходят, вводя ограничениеnmax на число итераций. Такое ограничение предохраняет от "зацикливания" метода, а также позволяет выявить практическое отсутствие сходимости вычислительного процесса.
Целью лабораторных работ, помещенных в данном разделе, является изучение перечисленных ранее четырех итерационных методов приближенного решения нелинейных уравнений, при этом каждая работа посвящена одному из них. Для выполнения работ предлагается использовать набор подпрограмм-функций, реализующих конкретные численные методы, а также подпрограмму-функцию Round, позволяющую моделировать ошибки в исходных данных. Указанные подпрограммы (языкC) размещаются в директорииLIBR1.
3.2. Метод бисекции
Если найден отрезок (a, b), такой, что
 (a)
(a) (b)<0,
то существует точкаc,
в которой значение функции равно нулю,
т. е.
(b)<0,
то существует точкаc,
в которой значение функции равно нулю,
т. е.
 (с)=0,с Î(a,
b).
Метод бисекции состоит в построении
последовательности вложенных друг в
друга отрезков, на концах которых
функция имеет разные знаки. Каждый
последующий отрезок получается делением
пополам предыдущего. Процесс построения
последовательности отрезков позволяет
найти нуль функции
(с)=0,с Î(a,
b).
Метод бисекции состоит в построении
последовательности вложенных друг в
друга отрезков, на концах которых
функция имеет разные знаки. Каждый
последующий отрезок получается делением
пополам предыдущего. Процесс построения
последовательности отрезков позволяет
найти нуль функции (корень уравнения
(корень уравнения )
с любой заданной точностью.
)
с любой заданной точностью.Рассмотрим один шаг итерационного процесса. Пусть на (n-1)-м шаге найден отрезок(an -1, bn -1)Ì(a,b), такой, что
 (an
-1)
(an
-1) (bn
-1)
<0.Разделим его пополам точкойx=(an
-1
+
bn
-1)
/
2и вычислим
(bn
-1)
<0.Разделим его пополам точкойx=(an
-1
+
bn
-1)
/
2и вычислим
 (x).
(x).Если
 (x)
=0,
то x=(
an
-1
+bn
-1)
/ 2- корень уравнения.
(x)
=0,
то x=(
an
-1
+bn
-1)
/ 2- корень уравнения.Если
 (x)¹0,
то из двух половин отрезка выбирается
та, на концах которой функция имеет
противоположные знаки, поскольку
искомый корень лежит на этой половине:
(x)¹0,
то из двух половин отрезка выбирается
та, на концах которой функция имеет
противоположные знаки, поскольку
искомый корень лежит на этой половине:an = an -1, bn = x, если
 (x)
(x) (an
-1)
< 0
;
(an
-1)
< 0
;an = x, bn = bn -1 , если
 (x)
(x) (an
-1)
> 0
.
(an
-1)
> 0
.Если требуется найти корень с точностью e, то деление пополам продолжается до тех пор, пока длина отрезка не станет меньше2e. Тогда координата середины отрезка и будет значением корня с требуемой точностью.
Метод бисекции является простым и надежным методом поиска простого корня уравнения
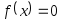 (простым называется кореньx
=
c дифференцируемой функции
(простым называется кореньx
=
c дифференцируемой функции ,
если
,
если
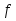 (с)= 0
и
(с)= 0
и
 (с)
¹0).
Этот метод сходится для любых непрерывных
функций
(с)
¹0).
Этот метод сходится для любых непрерывных
функций ,
в том числе недифференцируемых. Скорость
его сходимости невысока. Для достижения
точностиeнеобходимо
совершитьN
»
log2
(b
-
a)
/eитераций. Это означает, что для получения
каждых трех верных десятичных знаков
необходимо совершить около 10 итераций.
,
в том числе недифференцируемых. Скорость
его сходимости невысока. Для достижения
точностиeнеобходимо
совершитьN
»
log2
(b
-
a)
/eитераций. Это означает, что для получения
каждых трех верных десятичных знаков
необходимо совершить около 10 итераций.
