4. Степенные ряды
Степенным называется ряд вида
,
(8)
где сn – действительные числа, называемые коэффициентами ряда.
Для всякого
степенного ряда существует интервал
сходимости
,
или
с центром в точке а, внутри которого
степенной ряд абсолютно сходится и вне
которого он расходится. На концах
интервала сходимости (в точках
)
степенной ряд необходимо исследовать
отдельно. Число R
называется радиусом сходимости
степенного ряда. Если
,
то ряд (8) сходится лишь при
;
если же
,
то ряд (8) сходится на всей числовой оси.
Для нахождения интервала сходимости можно применять либо признак Даламбера, либо признак Коши, т.е.
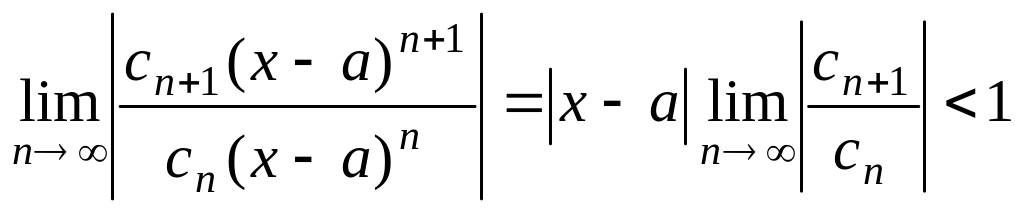
или
.
Тогда
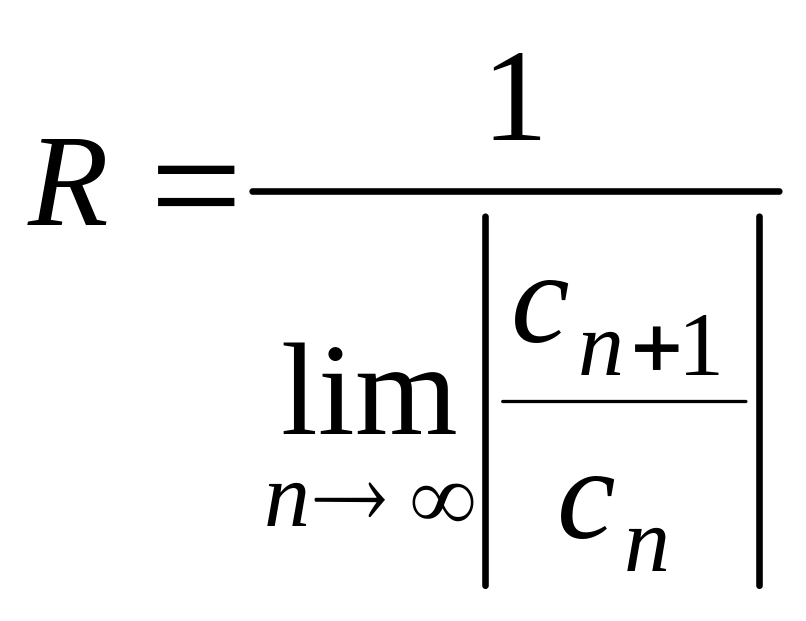или
.
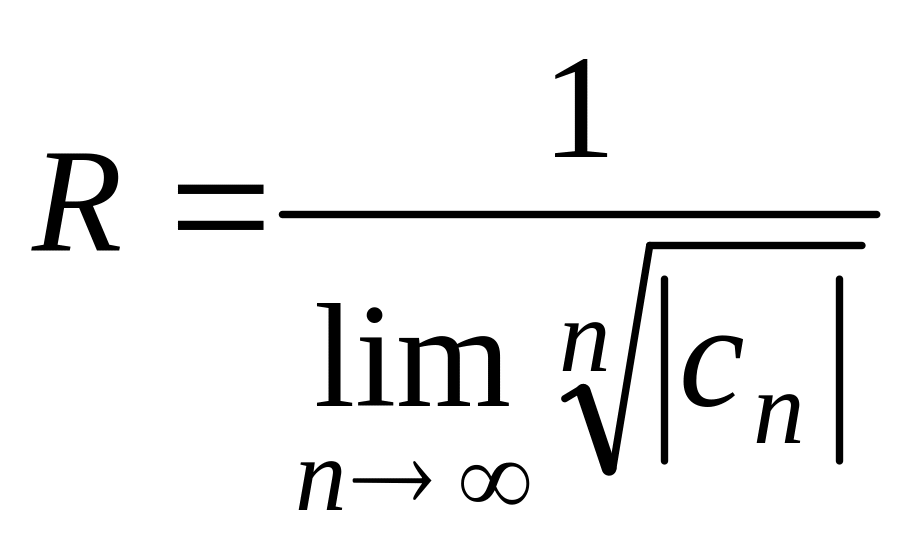Пример.
Найти область сходимости ряда
.
Решение.
Применяем признак Даламбера
.
Ряд сходится, когда полученный
предел меньше единицы, т.е.
.
При
ряд расходится. Радиус сходимости
;
интервал сходимости
.
Исследуем поведение ряда на концах
промежутка
.
При
получаем знакочередующийся ряд
.
Этот ряд удовлетворяет условиям признака
Лейбница, поэтому он сходится. При
получаем ряд
.
Полученный ряд расходится, так как
каждый его член больше соответствующего
члена гармонического ряда
.
Следовательно, областью сходимости
данного ряда является промежуток
.
Задачи.
Найти области сходимости степенных рядов:
12.37.
; 12.38.
;
12.39.
; 12.40.
;
12.41.
; 12.42.
;
12.43.
; 12.44.
;
12.45.
; 12.46.
;
12.47.
; 12.48.
.
5. Разложение функций в ряд Тейлора
Всякая функция,
бесконечно дифференцируемая в интервале
,
может быть разложена в этом интервале
в сходящийся к ней степенной ряд
Тейлора:
если в этом интервале выполняется условие
,
где
– остаток ряда Тейлора,
.
При
получается ряд Маклорена:
.
При решении многих задач рекомендуется пользоваться следующими разложениями в ряд Маклорена элементарных функций:
,
,
,
,
,
,
,
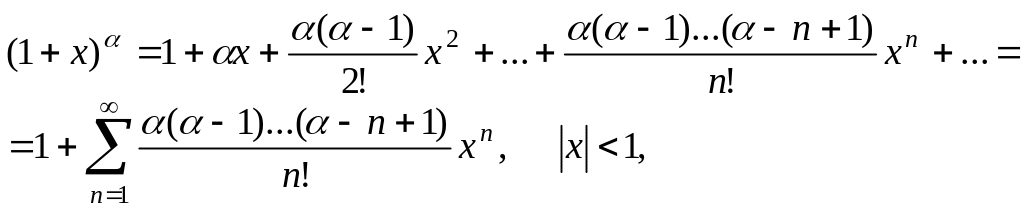
при
из предыдущего разложения получаем
бесконечную геометрическую прогрессию
со знаменателем
:
.
Пример.
Разложить в ряд по степеням х
функцию
.
Решение.
Найдем значения функции и ее
производных при
:
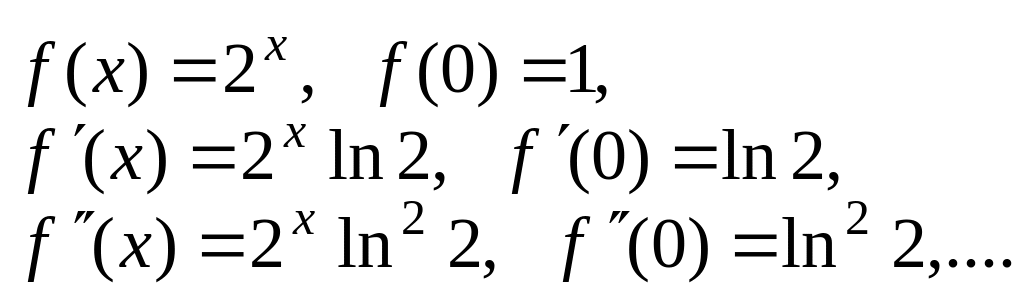
Следовательно,
Это разложение можно получить
иначе. Достаточно в разложении
заменить х на
,
так как
.
Пример.
Разложить в ряд по степеням
функцию
.
Решение.
Воспользуемся равенством
.
Правую часть этого равенства
можно рассматривать как сумму бесконечно
убывающей геометрической прогрессии
с первым членом
и знаменателем
.
Отсюда получаем
,
т.е.
Так как
,
то
-
область сходимости ряда.
Задачи.
Разложить в ряды по степеням х следующие функции:
12.49.
; 12.50.
;
12.51.
; 12.52.
;
12.53.
; 12.54.
.
Разложить в ряды по степеням
и определить области сходимости
полученных рядов:
12.55.
;
12.56.
;
12.57.
;
12.58.
.
6. Ряды Фурье
В естествознании и технике часто приходится иметь дело с периодическими процессами: колебательным и вращательным движением различных деталей машин и приборов, периодическим движением небесных тел и элементарных частиц, акустическими и электромагнитными колебаниями и т.п.
Математически
все такие процессы описываются
периодическими функциями. Простейшими
периодическими функциями являются
тригонометрические функции
и
с периодом
.
Основным вопросом настоящего раздела
является вопрос о представлении
произвольной периодической функции в
виде суммы тригонометрических функций.
Ряды Фурье
периода
.
Рядом Фурье периодической функции
с периодом
,
определенной на отрезке
,
называется тригонометрический ряд
, (9)
коэффициенты которого определяются формулами
, (10)
. (11)
Ряды Фурье
периода 2l.
Если периодическая функция
с периодом 2l
задана на отрезке
,
то при выполнении на этом отрезке условий
теоремы Дирихле указанная функция может
быть представлена в виде суммы ряда
Фурье
,
где
, (12)
. (13)
Ряд Фурье четной
функции содержит только свободный член
и косинусы
;
ряд Фурье нечетной функции содержит
только члены с синусами
.
Если функция
задана на отрезке
,
то для разложения в ряд Фурье достаточно
доопределить ее на отрезке
произвольным способом, а затем разложить
в ряд Фурье, считая ее заданной на отрезке
.
Наиболее целесообразно функцию
доопределить так, чтобы ее значения в
точках отрезка
находились из условия
или
.
В первом случае функция
на отрезке
будет четной, а во втором – нечетной.
Пример.
Разложить в ряд Фурье периодическую
функцию
с периодом
,
заданную на интервале
.
Решение.
Определяем коэффициенты ряда Фурье по формулам (10) и (11).
.
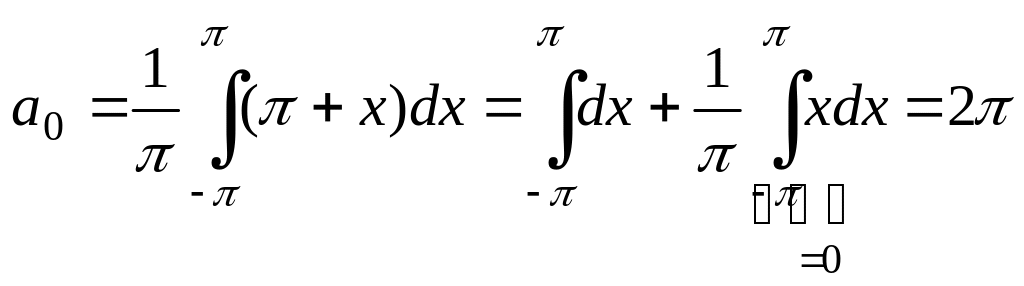Далее, находим коэффициенты
:
.
Первый интеграл равен нулю, т.к.
Второй интеграл равен нулю, как интеграл от нечетной функции, взятый по интервалу, симметричному относительно начала координат.
Найдем теперь коэффициенты
:
.
Первый интеграл равен нулю, как интеграл от нечетной функции. Подынтегральная функция второго интеграла – четная как произведение двух нечетных функций. Таким образом,
Следовательно, разложение функции в ряд Фурье имеет вид
.
Задачи.
Разложить в ряд Фурье следующие функции периода l:
12.59.
;
12.60.
;
12.61.
.
12.62.
;
12.63.
;
12.64.
;
12.65.
;
12.66.
.
Ответы
12.1.
Расходится 12.2.
Сходится 12.3.
Сходится 12.4.
Расходится 12.5.
Расходится 12.6.
Сходится 12.7.
Сходится 12.8.
Сходится 12.9.
Расходится 12.10.
Расходится 12.11.
Расходится 12.12.
Сходится 12.13.
Сходится 12.14.
Расходится 12.15.
Сходится
12.16.
Сходится 12.17.
Расходится 12.18.
Сходится 12.19.
Сходится 12.20.
Расходится 12.21.
Расходится 12.22.
Сходится 12.23.
Сходится условно 12.24.
Сходится абсолютно 12.25.
Расходится 12.26.
Сходится абсолютно 12.27.
Расходится 12.28.
Расходится 12.29.
Сходится 12.30.
Расходится 12.31.
Расходится 12.32.
Сходится 12.33.
Расходится 12.34.
Сходится 12.35.
Сходится условно 12.36.
Сходится абсолютно 12.37.
х
= 5 12.38.
(-,+)
12.39.
[1,3] 12.40.
12.41.
[-2,2]
12.42.
(-,+)
12.43.
[3,5) 12.44.
(-1,3) 12.45.
x
= 0 12.46.
(-,+)
12.47.
(-1,1) 12.48.
[-1,1] 12.49.
12.50.
12.51.
12.52.
12.53.
12.54.
12.55.
12.56.
12.57.
12.58.
12.59.
12.60.
12.61.
12.62.
12.63.
12.64.
12.65.
12.66.
.
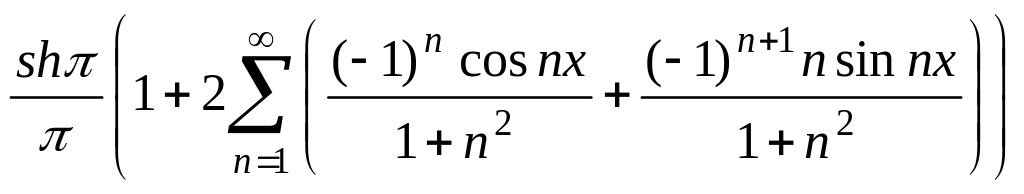