
- •Кафедра математики и естественнонаучных дисциплин Борисова о.Н. Интегральное исчисление функций одной переменной
- •Введение
- •Неопределённый интеграл
- •Замена переменной
- •Интегрирование по частям
- •2) Интеграл вида , , .
- •3) Интеграл вида , .
- •Интегрирование рациональных функций
- •Интегрирование иррациональных функций
- •4) Избавление от иррациональности с помощью тригонометрических подстановок
- •2) Универсальная тригонометрическая подстановка.
- •Определенный интеграл
- •Замена переменной.
- •Интегрирование по частям.
- •Приложение определённого интеграла.
- •1) Площадь криволинейного сектора.
- •Контрольная работа №1
- •Решение варианта 0
- •Решение варианта 0
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант №13
- •Вариант №15
- •Вариант №23
- •Вариант №25
4) Избавление от иррациональности с помощью тригонометрических подстановок
В выражениях
![]() ,
,
![]() ,
,
![]() можно избавиться от радикалов, заменяя
x на подходящую
тригонометрическую функцию. Список
замен приведен в таблице.
можно избавиться от радикалов, заменяя
x на подходящую
тригонометрическую функцию. Список
замен приведен в таблице.
-
Интеграл
Замена
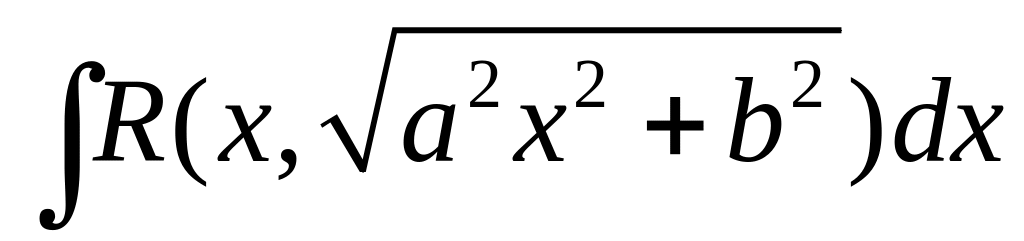
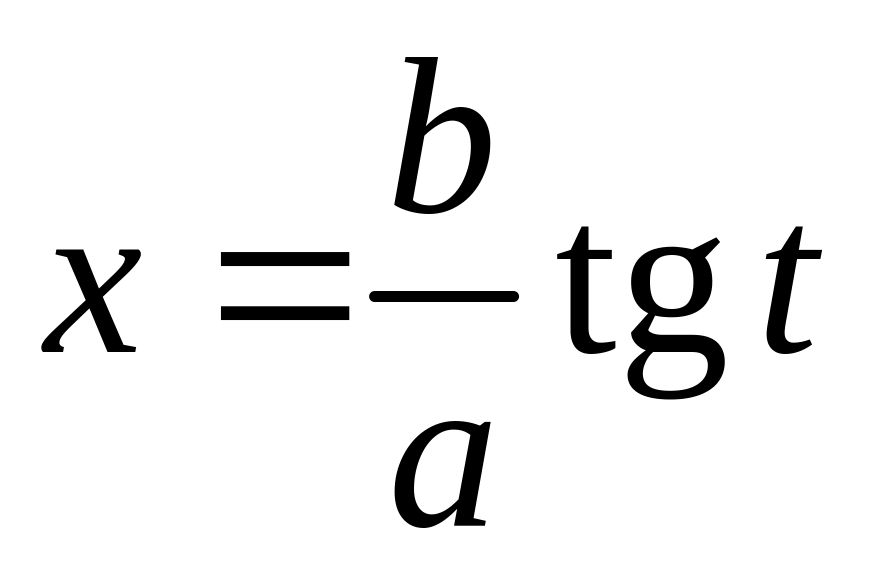
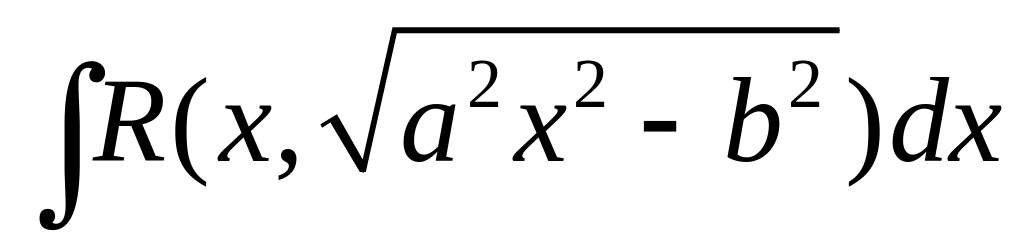
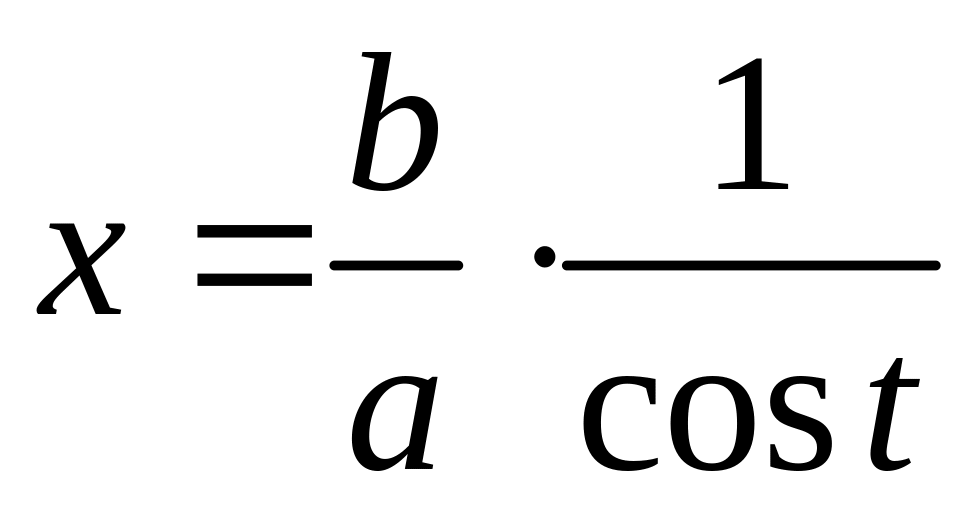
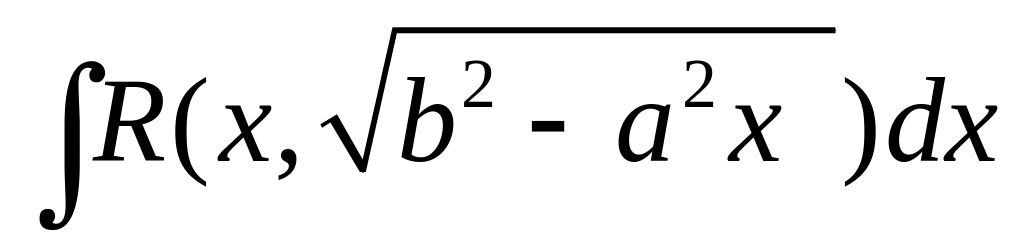
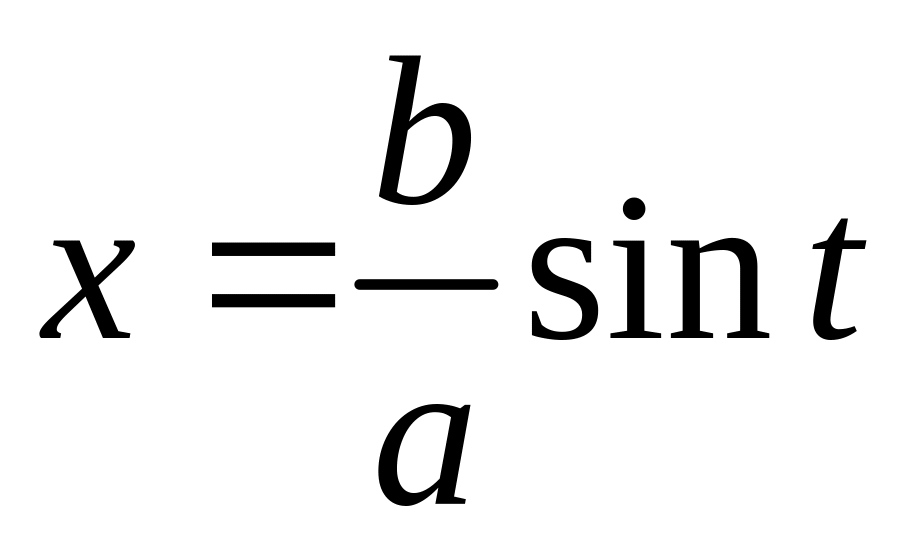
Примеры.
i)
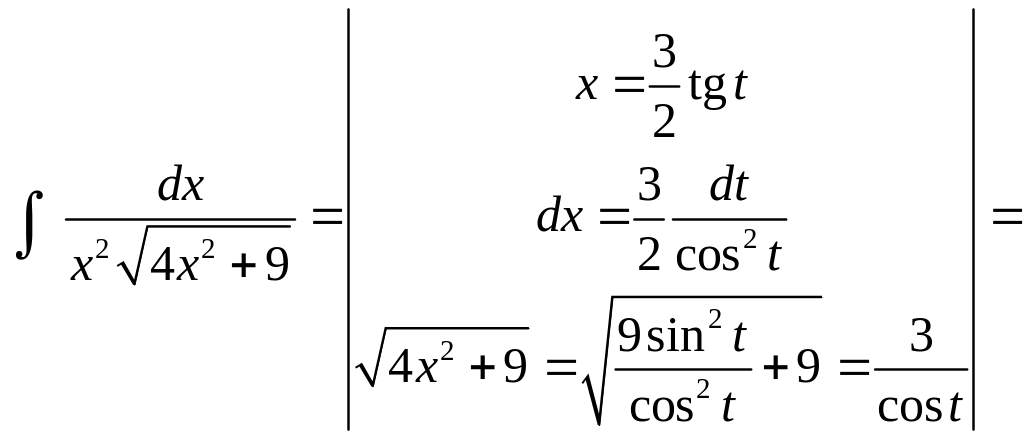
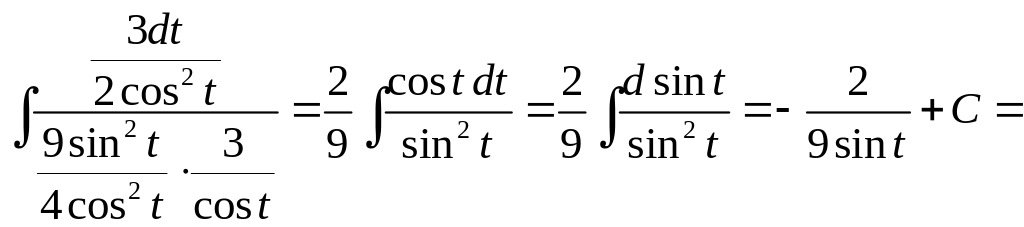
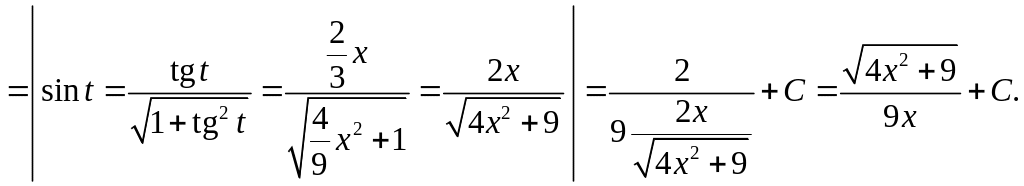
ii)
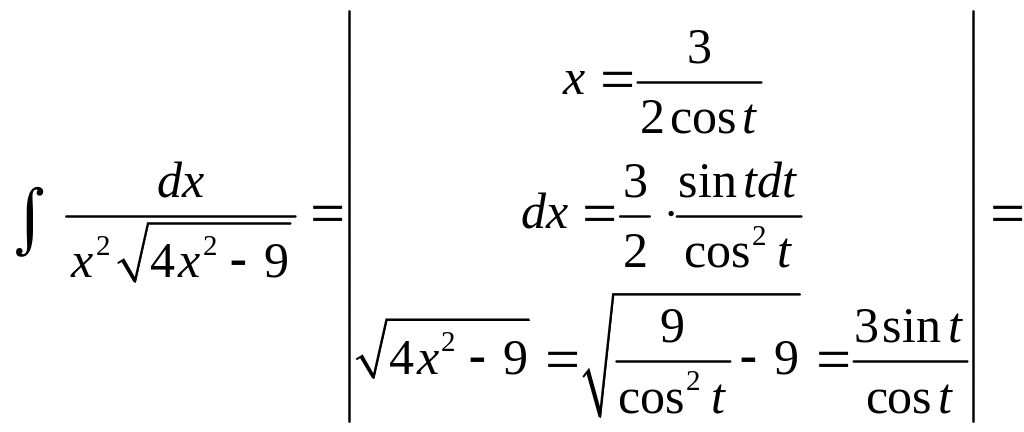
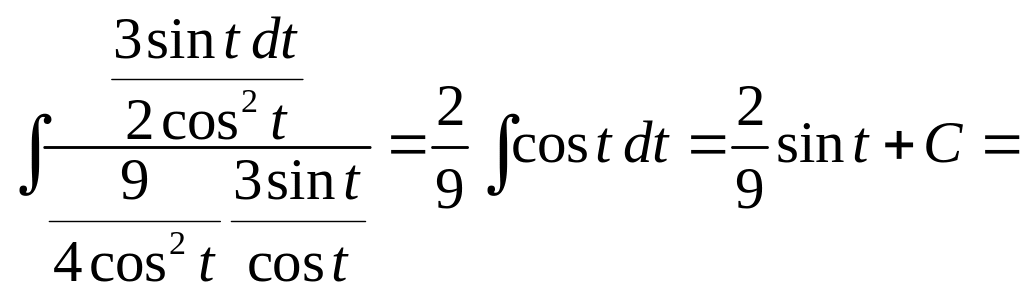
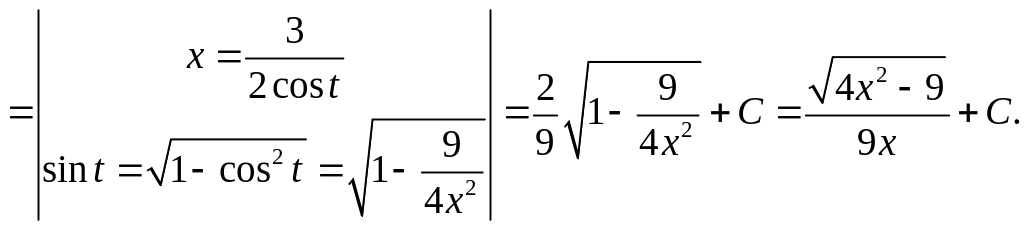
iii)
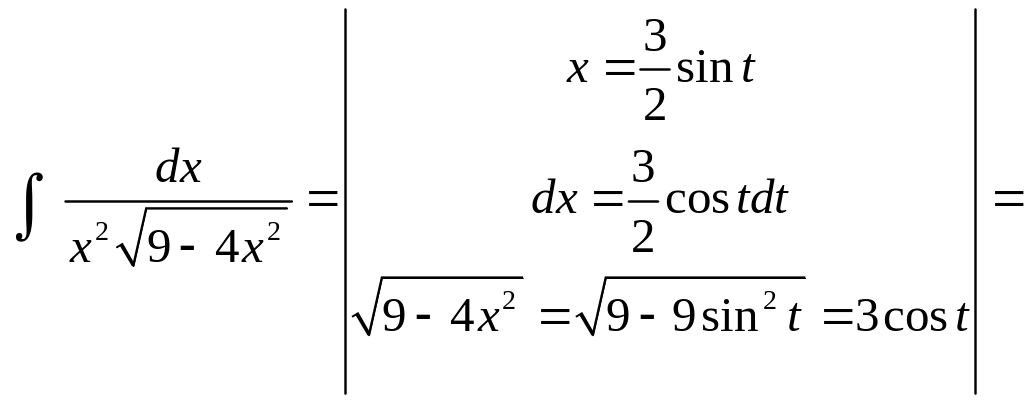
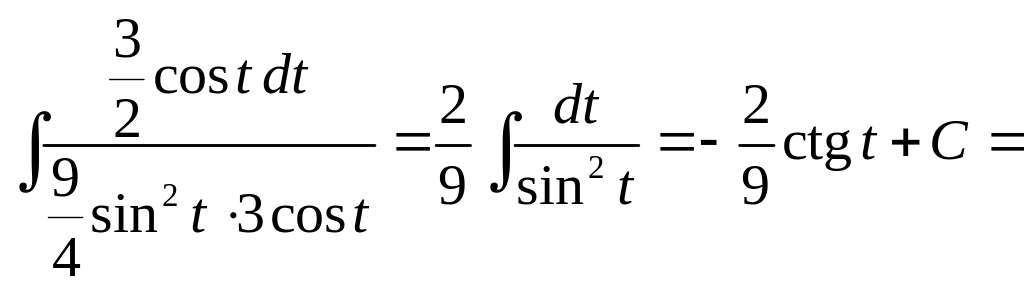

5) Подстановки Эйлера. Подстановки
Эйлера помогают избавиться от
иррационального вида
![]() .
.
Пример.
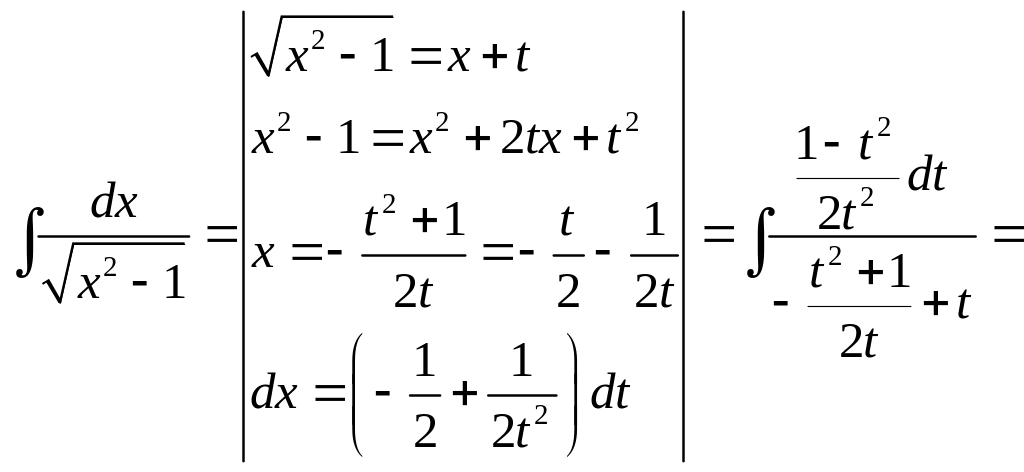
![]()
Интегрирование рациональных функций от sin x и cos x.
1) Интегралы вида
![]() ,
,
![]() ,
,
![]() .
.
Различают два случая:
а) хотя бы одно из чисел p или q нечетно; тогда в качестве новой переменной интегрирования берут функцию sin x (если q нечетно) или cos x (если p нечетно).
б) если p и q оба четны, делают замену t = tg x или t = ctg x.
Примеры. i)
![]()
![]()
![]()
ii)
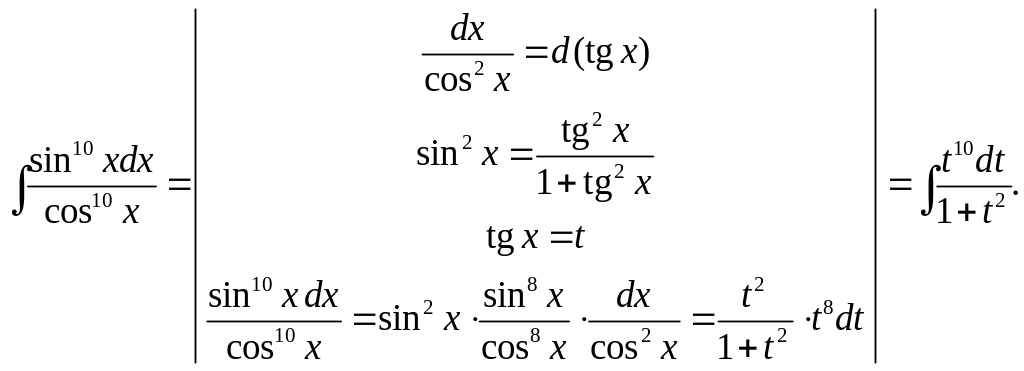
Поделим
![]() на
на
![]() с остатком:
с остатком:
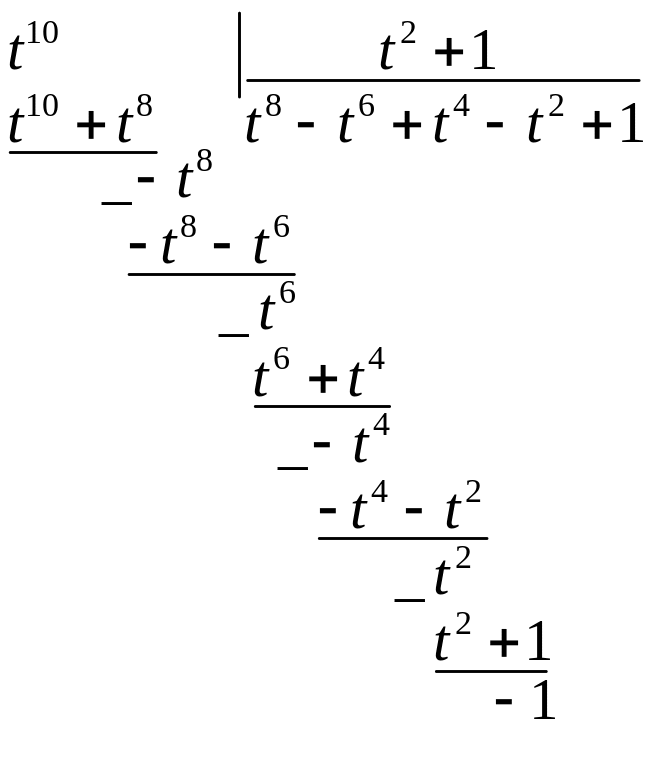
Таким образом
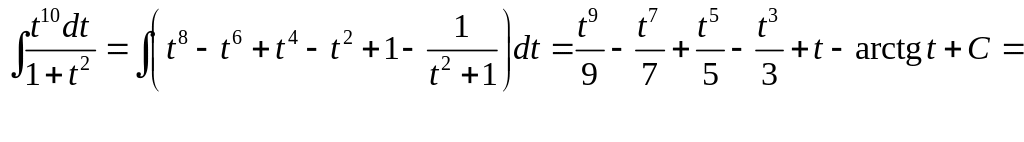
![]()
2) Универсальная тригонометрическая подстановка.
Из курса тригонометрии известно, что
функции sin x
и cos x
можно выразить как рациональные функции
от
![]() :
:
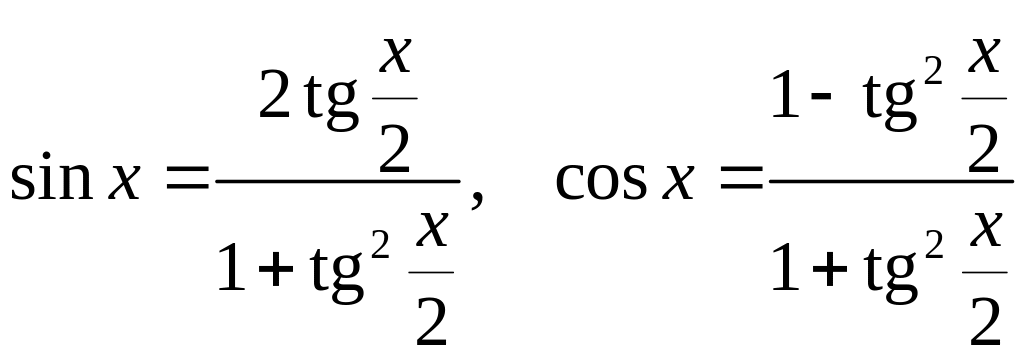 .
.
Замена
![]() ,
,
![]() ,
,
![]() называется универсальной
тригонометрической подстановкой.
называется универсальной
тригонометрической подстановкой.
Пример.
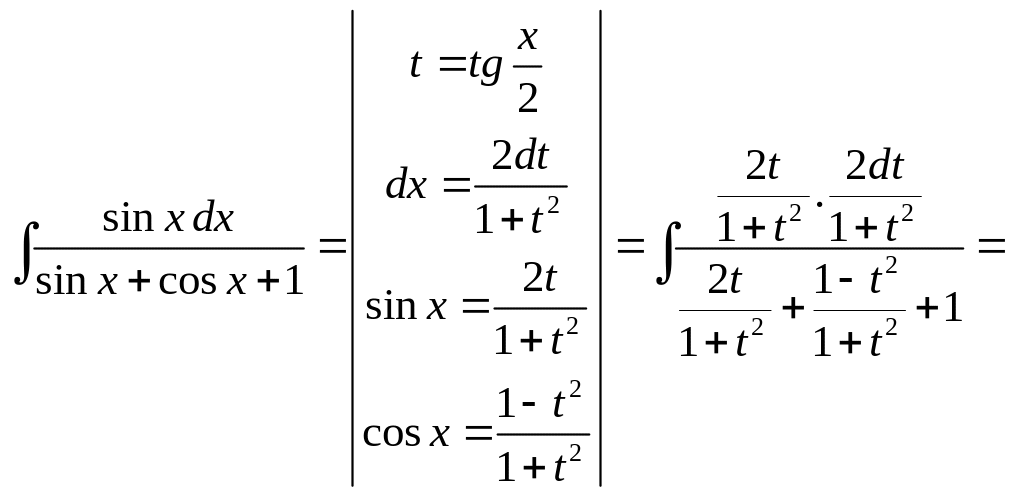
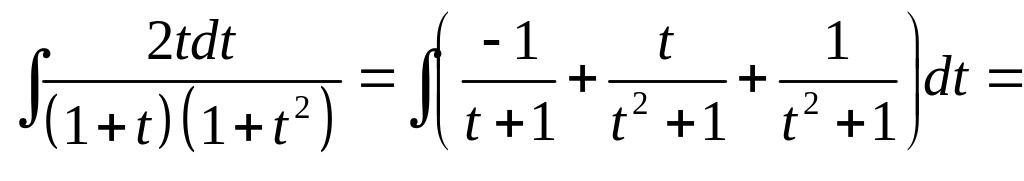
![]()
Определенный интеграл
Определенный интеграл (Римана) позволяет распространить формулу площади прямоугольника на площадь более или менее произвольной плоской геометрической фигуры. В основе понятия определенного интеграла лежит так называемая интегральная сумма, определяемая следующим образом.
Пусть функция y =
f(x)
определена на отрезке [a,b].
Разобьем отрезок [a,b]
на n частей [x0,x1],
[x1,x2],
…, [xn1,xn]
(x0 = a,
xn
= b) произвольным
образом. В частности, можно разбить
[a,b]
на n равных частей,
тогда длина каждого отрезка разбиения
будет равна
![]() .
В общем случае, пусть
.
В общем случае, пусть
![]() .
Возьмем опять же произвольным образом
внутри каждого из отрезков [xi1,xi]
по точке
.
Возьмем опять же произвольным образом
внутри каждого из отрезков [xi1,xi]
по точке
![]() .
Интегральной суммой функции на
[a,b]
по разбиению τ = (n,
x0, x1,
..., xn,
.
Интегральной суммой функции на
[a,b]
по разбиению τ = (n,
x0, x1,
..., xn,
![]() ,
…,
,
…,
![]() )
называется число
)
называется число
![]() .
.
 y
y
![]()
y = f(x)
a xi−1 i xi b x
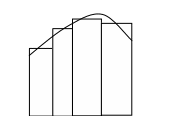
Если
![]() ,
то интегральная сумма есть площадь
фигуры, состоящей из прямоугольников
со сторонами (
,
то интегральная сумма есть площадь
фигуры, состоящей из прямоугольников
со сторонами (![]() )
и
)
и
![]() ,
i = 1, ..., n.
Интуитивно ясно, что чем меньше
максимальная длина отрезков разбиения
,
i = 1, ..., n.
Интуитивно ясно, что чем меньше
максимальная длина отрезков разбиения
![]() ,
тем точнее эта фигура из прямоугольников
приближает криволинейную трапецию с
основаниями x = a,
x = b
и «боковыми сторонами» y
= f(x),
y = 0. Интеграл от
f(x)
по отрезку [a,b]
есть предел от I(τ)
по всевозможным разбиениям τ, когда
,
тем точнее эта фигура из прямоугольников
приближает криволинейную трапецию с
основаниями x = a,
x = b
и «боковыми сторонами» y
= f(x),
y = 0. Интеграл от
f(x)
по отрезку [a,b]
есть предел от I(τ)
по всевозможным разбиениям τ, когда
![]() 0.
Предел понимается здесь в обычном
смысле: число I
называется определенным интегралом
от f(x)
по [a,b]
(и обозначается как
0.
Предел понимается здесь в обычном
смысле: число I
называется определенным интегралом
от f(x)
по [a,b]
(и обозначается как
![]() ),
если для произвольного
),
если для произвольного
![]() > 0 найдется такое
> 0 найдется такое
![]() >0,
что, как только разбиение τ отрезка
[a,b]
удовлетворяет условию
>0,
что, как только разбиение τ отрезка
[a,b]
удовлетворяет условию
![]() ,
интегральная сумма
,
интегральная сумма
![]() ,
отвечающая этому разбиению, отличается
от I не больше, чем на
,
отвечающая этому разбиению, отличается
от I не больше, чем на
![]()
![]()
Геометрический смысл определенного
интеграла заключается в том, что
![]() есть (с точностью до знака) площадь
криволинейной трапеции, заключенной
между графиком функции y
= f(x),
осью абсцисс и прямыми x
= a, x
= b. В частности, если
на отрезке [a,b]
заданы две функции f(x)
и g(x),
есть (с точностью до знака) площадь
криволинейной трапеции, заключенной
между графиком функции y
= f(x),
осью абсцисс и прямыми x
= a, x
= b. В частности, если
на отрезке [a,b]
заданы две функции f(x)
и g(x),
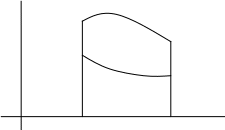
![]() ,
то площадь криволинейной трапеции,
заключенной между графиками этих двух
функций, равна
,
то площадь криволинейной трапеции,
заключенной между графиками этих двух
функций, равна
![]()
 y
y
y=f(x)
y=g(x)
a b x
Связь между определенным и неопределенным интегралом заключена в форуме Ньютона–Лейбница:
![]() ,
,
где F(x)
– произвольная первообразная функции
f(x).
Разность значения функции F(х)
в двух точках a и b
принято обозначать так:
 .
Справедливы следующие две формулы –
замена переменной интегрирования и
интегрирование по частям.
.
Справедливы следующие две формулы –
замена переменной интегрирования и
интегрирование по частям.
