[Математические методы обработки эксперимента стр.27-41]

3.3. Дисперсионный анализ

Во многих случаях нас интересует вопрос о том, в какой мере существенно влияние того или иного фактора или комбинации фак­торов. Решение подобных задач составляет предмет дисперсионного анализа, разработанного английским статистиком Р. А. Фишером.

В случае многофакторного опыта при помощи дисперсионного анализа определяются дисперсии, обусловленные действием каж­дого фактора в отдельности и их взаимодействиями, и оценивается статистическая значимость этих величин с учетом ошибки воспро­изводимости.

Дисперсионный анализ можно производить только, когда выпол­няются следующие условия:

- серии измерений можно рассматривать как случайные выборки из генеральных сово - купностей, подчиняющихся нормальному рас­пределению;

- дисперсии, обусловленные ошибками воспроизводимости, для всех серий измерений однородны.

Нет необходимости предъявлять жесткие требования к проверке первого из этих условий, так как F-критерий оказывается приме­нимым и тогда, когда имеется неслучайное нарушение нормального распределения; важно только, чтобы мы не имели дело с каким-либо распределением, существенно отличным от нормального.

Второе из указанных выше условий должно выполняться до­статочно строго. Если нет уверенности в том, что рассматривае­мые серии измерений являются выборками из генеральных сово­купностей с одной и той же дисперсий, обусловленной ошибками воспро-изводимости, то следует проверить однородность дисперсий, пользуясь критериями Кохрена или Н-критерием.

Рассмотрим некоторые из простей­ших приемов дисперсионного анализа, находящих применение в раз­нообразных областях науки и техники.

Однофакторный дисперсионный анализ

Пусть, например, при совместном анализе точности группы из­мерительных приборов — потенциометров — нас интересует вопрос о том, можно ли считать их систематические ошибки одинаковыми. Иначе говоря, мы хотим проверить влияние одного фактора — прибора — на погрешность показаний. Пусть число потенциомет­ров будет т и каждый из них измеряет напряжение одного и того источника п раз (табл. 3.4).

Таблица 3.4

Расположение материала при определении дисперсии, обусловленной действием

Одного фактора

№ -измерения	№ прибора
	1	2	….	т
1 2 .	х11 х12 …	х21 х22 …….	. . .	хm1 хm2 …
п	х1n	х2n	. . .	хmn
Итого			. . .

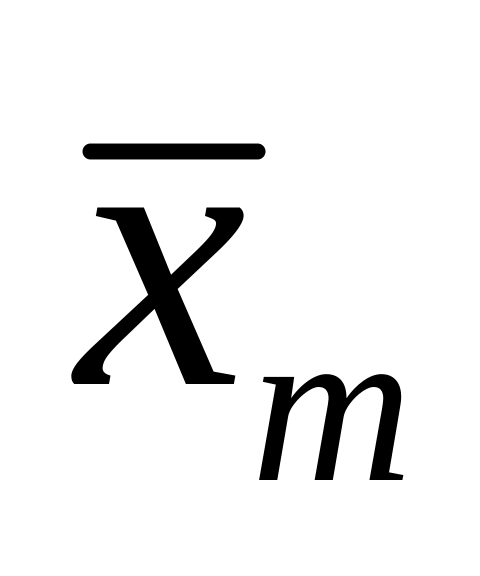
При таком расположении материала рассеяние между строч­ками будет определяться ошибкой воспроизводимости, а рассеяние между столбцами — систематическими ошибками приборов.

Чтобы оценить ошибку воспроизводимости, подсчитаем диспер­сию по каждому столбцу в отдельности, а затем среднюю дисперсию

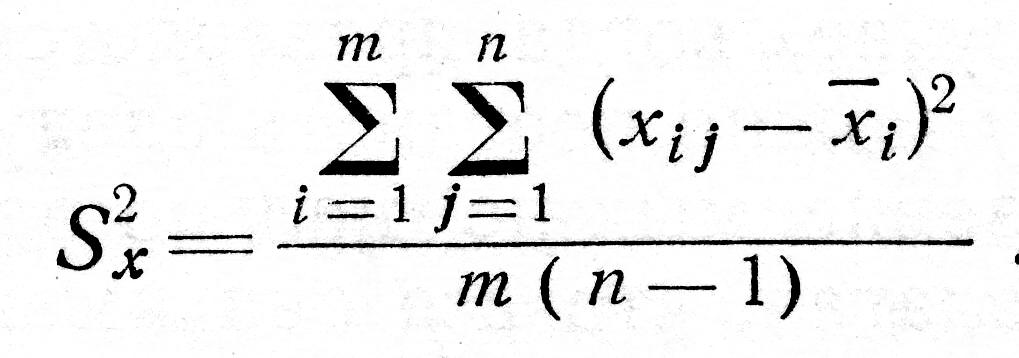(3.22)

Средняя дисперсия по отношению к общему среднему по всей таблице равна сумме двух дисперсий: дисперсии , обус­ловленной различной работой приборов, и дисперсии, обусловленной ошибкой воспроизводимости σ_восп, деленной на число параллельных определений (число строк в столбце),

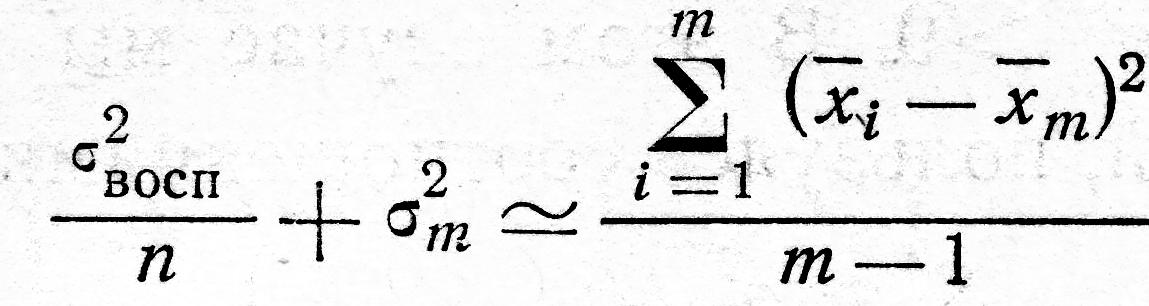(3.23)

Обычно для упрощения вычислений находят следующие вспомо­гательные суммы:

сумму квадратов всех значений

,

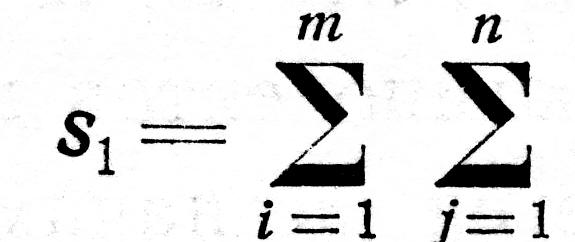сумму квадратов итогов по столбцам, деленную на число данных,

,

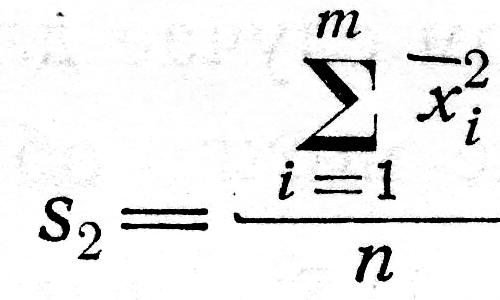квадрат общего итога, деленный на общее число данных

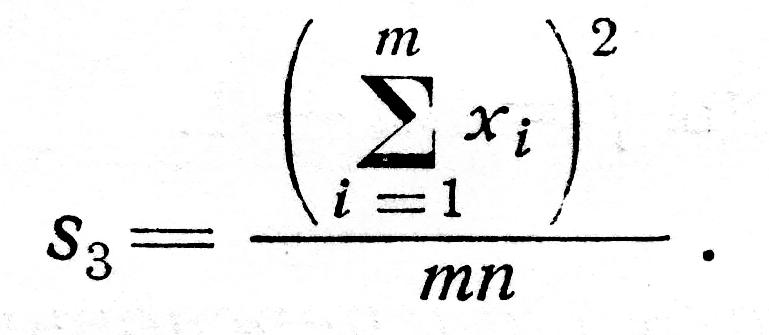
Результаты расчетов представляются так, как это показано в табл.3.5.

Таблица 3.5

Представление результатов дисперсионного анализа

Рассеяние	Суммы квадратов	Число степеней свободы	Дисперсии	Компоненты генеральных дисперсий
Между столбцами Между строчками Сумма	s2– s3 s1– s2 s1– s3	т — 1 m(n—1) mn—1	–	–

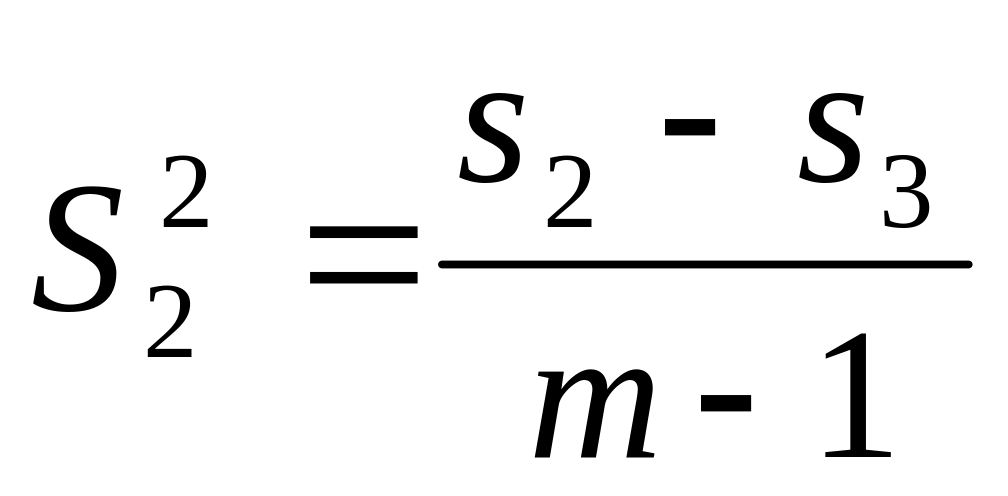
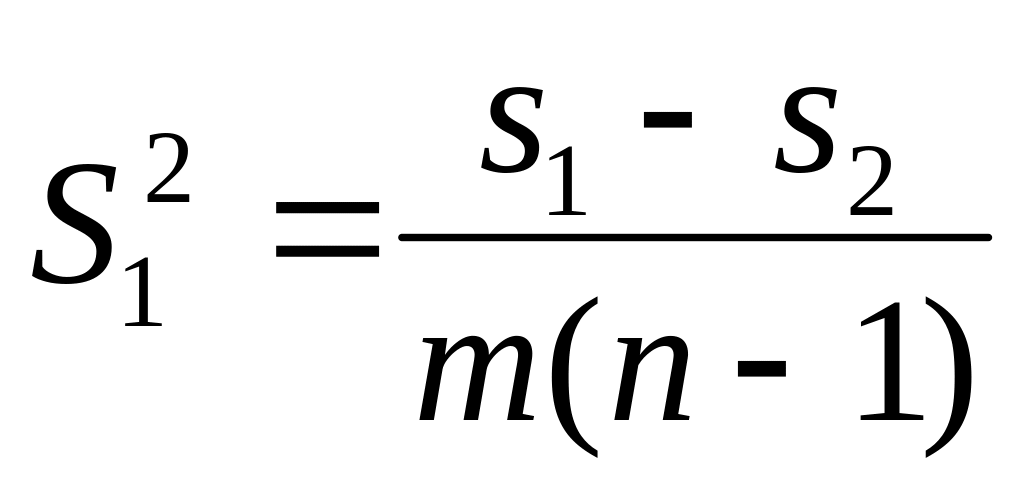
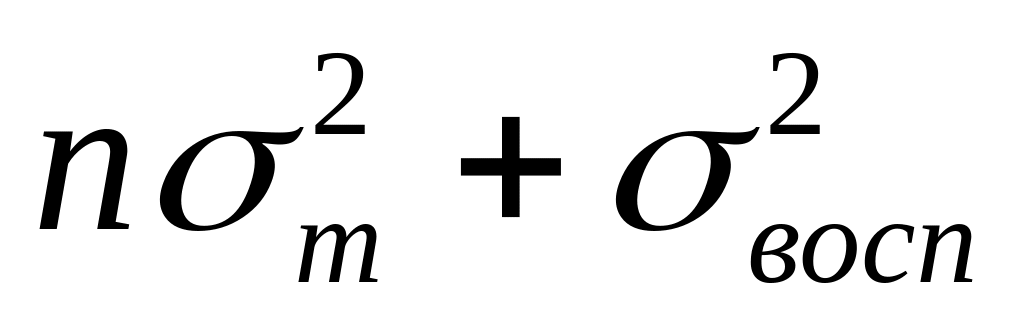
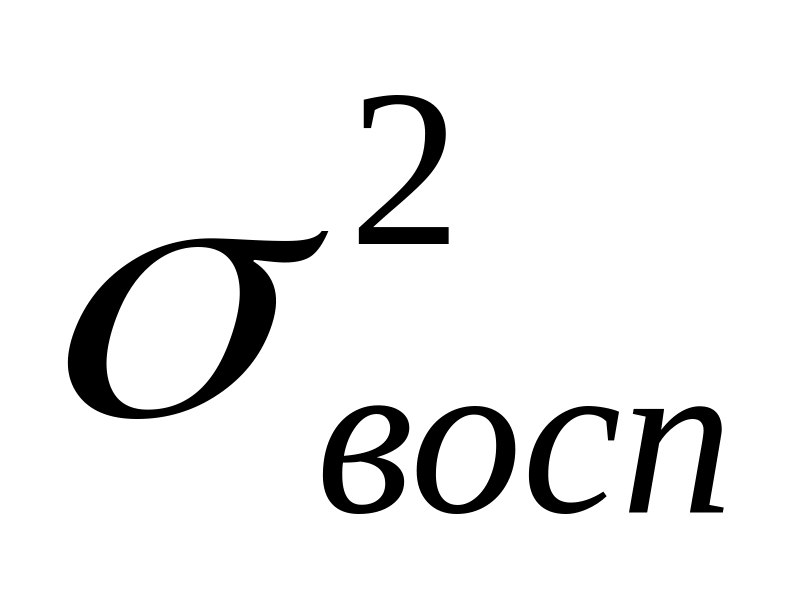
Прежде чем приступить к определению компонентов дисперсий, нужно убедиться в значимости отношения

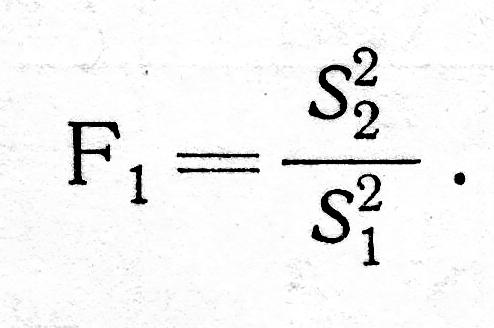
С этим отношением связаны два значения числа степеней сво­боды:

- для числителя т—1,

- для знаменателя т (п—1).

Если F₁>F_0,05 при f₁ = т—1 и f₂ = т (п—1), то с 5%-ным риском сде­лать ошибку мы можем утверждать, что . Это может быть только тогда, когда >0. В этом случае мы можем определить компоненты дисперсий, пользуясь соотношениями

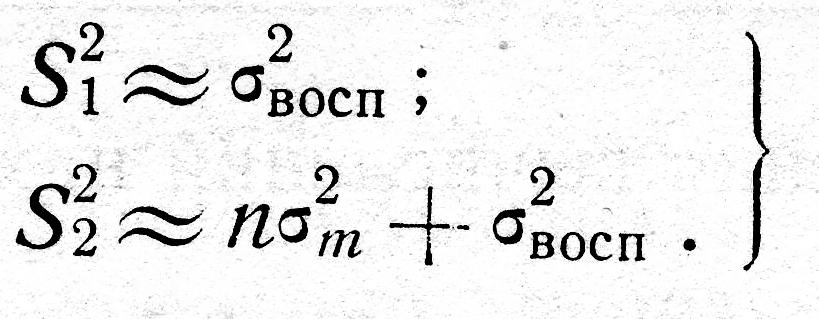
Если значение F₁ окажется незначимым, то мы вынуждены будем принять нуль-гипотезу ( =0). Тогда мы можем считать, что все т групп наблюдений извлечены из одной и той же гене­ральной совокупности. В этом случае для дисперсии получим две

оценки и , которые можно объединить в дисперсию

(3.24)

при числе степеней свободы f = тп— 1.

Когда число факторов больше одного, т. е. при двух-, трех- и многофакторном анализе, процедура остается принципиально та­кой же, как и при однофакторном анализе, но соответственно ус­ложняются выкладки.

Планирование экспериментов при помощи дисперсионного ана­лиза имеет следующие преимущества по сравнению с традицион­ными классическими приемами исследований:

- при оценке действия каждого фактора определяется значимость эффекта, которую можно рассматривать как меру надежности по­лученных результатов;

- в комплексных опытах удается оценить эффекты взаимодейст­вия факторов, которые невозможно обнаружить при классической постановке экспериментов;

- в многофакторном дисперсионном анализе каждый результат служит для оценки всех факторов, а не одного, как это имеет место при традиционном планировании эксперимента.

Применение дисперсионного анализа дает возможность сокра­тить число экспериментов.