Обыкновенные дифференциальные уравнения

• Уравнения, связывающие независимые переменные, искомую функцию и её производные называется дифференциальными уравнениями.

Если искомая функция есть функция одного переменного , то ДУ называется обыкновенным.

• Наивысший порядок производной, входящей в ДУ, называется порядком этого уравнения.

	Способы задания ДУ
	явное	неявное
ДУ 1−ого порядка
ДУ 2−ого порядка
ДУ n−ого порядка

В ДУ n−ого порядка могут и не входить независимая переменная x, искомая функция и отдельные производные искомой функции, которые имеют порядок, меньший, чем n.

• Решением ДУ называется функция 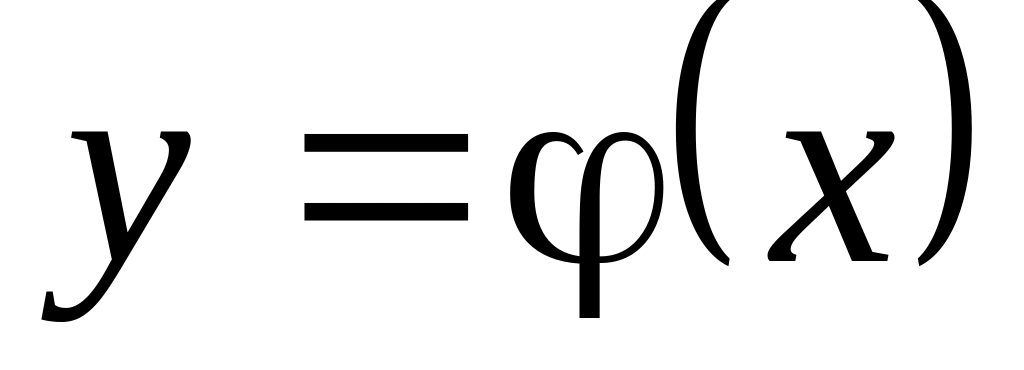, которая при подстановке в уравнение обращает его в верное тождество.

Процесс отыскания решения ДУ называется его интегрированием, а график решения ДУ – интегральной кривой.

Процесс отыскания решения ДУ, удовлетворяющего начальным условиям: ; ; … называется задачей Коши.

Точки, через которые проходят несколько интегральных кривых или ни одной, называются особыми.

Дифференциальные уравнения 1−ого порядка

• Функция называется общим решением ДУ , если:

1. : Функция является решением ДУ;

2. Каково бы не было начальное условие , существует единственное значение такое, что функция удовлетворяет данному начальному условию.

• Частным решением ДУ 1-ого порядка называется любая функция , полученная из общего решения при конкретном значении постоянной .

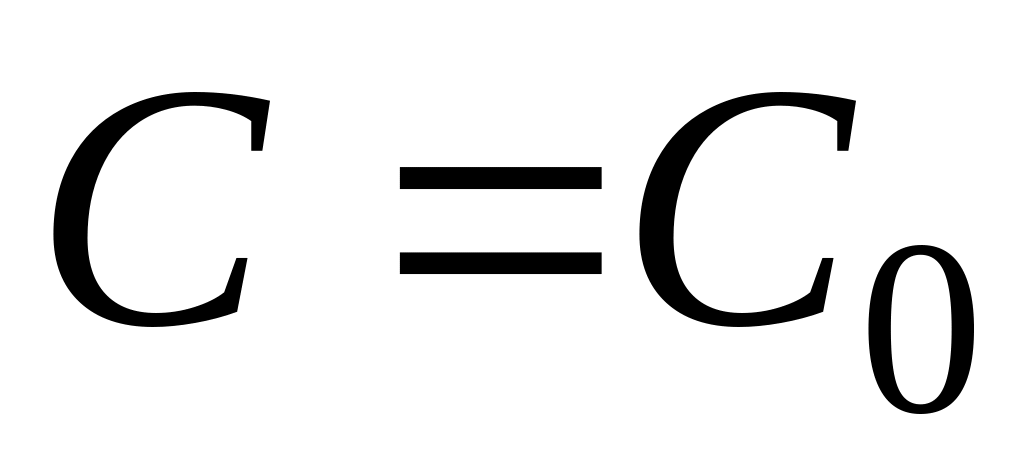− уравнение в дифференциалах.

Ду в полных дифференциалах

Полный дифференциал функции двух переменных имеет вид:

.

• ДУ , где левая часть равенства есть полный дифференциал функции в некоторой области, называется уравнением в полных дифференциалах: .

Тогда решением ДУ является выражение вида

Алгоритм решения:

Функцию можно восстановить из условий : ; . Тогда . Т. о. решением исходного ДУ есть выражение .

Однородные ду

• Функция называется однородной степени k, если .

• ДУ называется однородным, если функции , 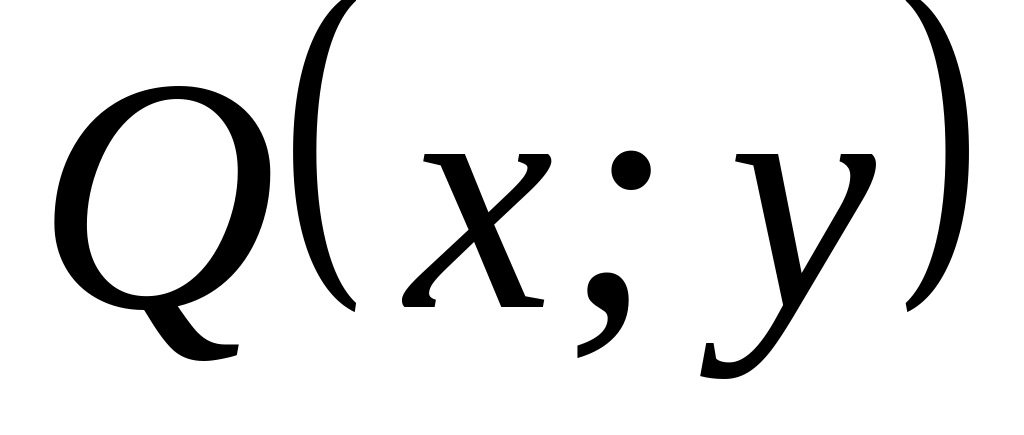являются однородными одной и той же степени.

Алгоритм решения:

Введем замену , тогда
	.
При подстановке в исходное уравнение получим ДУ с разделяющимися переменными, которое решим интегрированием относительно функции . Возвращаясь к замене, получим решение исходного ДУ.

ДУ, ПРИВОДЯЩИЕСЯ К ОДНОРОДНЫМ:
Составим систему линейных уравнений:
Если , то система имеет единственное решение . Введем замену Исходное уравнение сведется к однородному ДУ.	Если , то Введем замену , и получим ДУ 1-ого порядка с разделяющимися переменными.