Вычисление расхода воды

№ скоростной вертикали	Средняя скорость течения в м/сек		Площадь живого сечения между скоростными вертикалями, м2	Частичный расход воды в м3/сек
	на вертикали	между вертикалями

Измеренные и вычисленные скорости течения в створе реки служат одной из составных частей вычисления расхода воды.

Второй составной частью, как это следует из названия метода вычисления расхода воды, является площадь водного сечения. Она определяется по данным промеров на промерных вертикалях (рис. 8.4.).

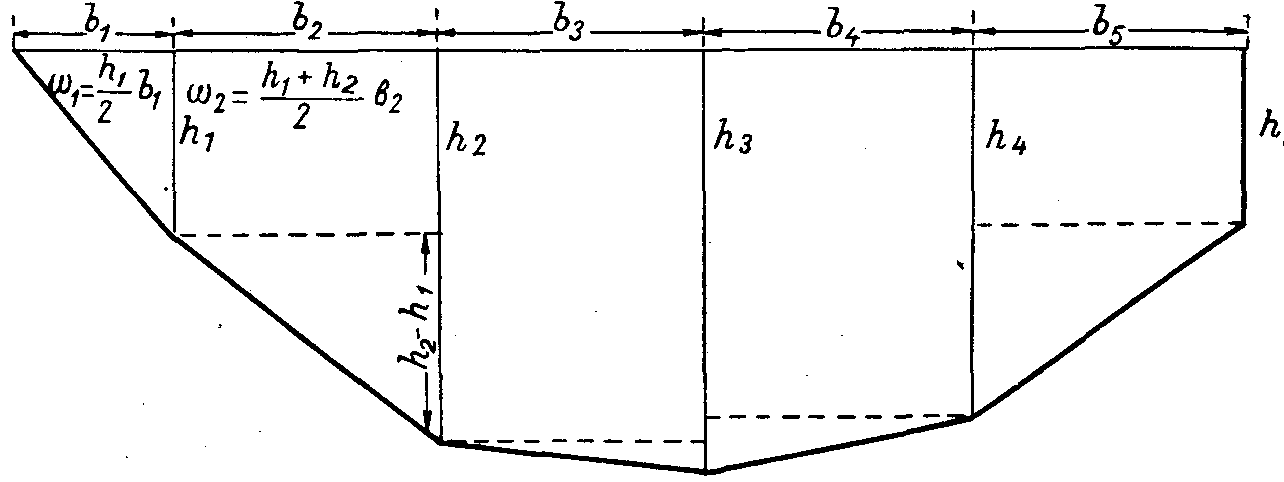
Рис.8.4 . Схема вычисления площади водного сечения.

Как видно из рисунка, промерные вертикали разбивают водное сечение на ряд трапеций, и только береговые участки могут иметь форму прямоугольного треугольника, если глубина на урезе воды равна нулю. Площадь каждой отдельной трапеции профиля в общем виде может быть выражена формулой:

(8.3.)

Аналитический способ. При аналитическом способе расходы воды вычисляются суммированием частных расходов воды. Приближенная формула согласно [5] имеет вид:

, м³/сек (8.4.)

где Q — расход воды, м^з /сек•;

V,V₂,..., V_n — средние скорости на вертикалях 1, 2….n, м/сек.;

—площадь живого сечения между берегом (границей мертвого пространства) и первой скоростной вертикалью, м²;

— площадь живого сечения между вертикалями 1 и 2 в м²;

— площадь живого сечения между последней скоростной вертикалью и берегом или границей мертвого пространства в м²;

k—коэффициент, величина которого для различных случаев принимается следующей:

- пологий берег с нулевой глубиной на урезе:….0,7;

- обрывистый берег или неровная стенка: ……..0,8;

- гладкая стенка: ....................................................0,9;

- наличие мертвого пространства:........................0,5.

В формуле расхода воды каждое слагаемое представляет собой частичный расход воды. Первое слагаемое - частичный расход между берегом и первой скоростной вертикалью, второе слагаемое - частичный расход между первой и второй вертикалями и т. д. Величина каждого частичного расхода вычисляется путем умножения средней скорости на площадь части живого сечения, соответствующей данному частичному расходу. Таким образом, для вычисления расхода необходимо определить средние скорости течения на каждой скоростной вертикали и частичные площади живого сечения.

Задание № 4. «Вычисление ежедневных расходов воды по измерениям на водомерном посту».

Исходные данные: Данные для расчета приведены в задании № 3.

Вычислить: ежедневные расходы воды по измерениям на водомерном посту.

В течение года на всех водомерных постах сети Росгидромета измеряются ежедневно уровни воды и периодически расходы воды. Измерения расходов воды выполняются через определенные периоды времени в зависимости от изменения амплитуды уровней (при значительном изменении уровня измерения производятся чаще, при незначительном – реже).

Все сведения, необходимые для подсчета ежедневных расходов воды сводятся в единую таблицу 8.4.

Зависимость между расходом воды и уровнем выражается кривой расхода, которая строится для определения стока воды. Стоком называется количество воды, протекающее через поперечное сечение водотока за некоторое время. Вычисление стока производится, как правило, ежегодно за прошедший год. Внутри годового цикла обычно приходится выделять отдельные периоды, для которых сток вычисляется различными методами, например: период ледостава, период развития водной растительности и др.

В гидрометрии принято определять зависимость Q=f(H), т. е. расходов от уровней, хотя фактически независимой переменной является расход, а уровень — функцией. Так принято ввиду того, что измерения уровней производятся чаще (обычно два раза в день), чем измерения расходов воды вследствие большой трудоемкости. На практике для вычисления стока расходы определяются в зависимости от наблюденных уровней, для чего и строится кривая расходов, или зависимость Q=f(H).

Таблица 8.4.

Пример таблицы измеренных расходов воды.

№ рас-хода	Дата изме-ре- ния	№ створа	Состоя-ние реки на участ-ке гидро-створа	Уровень воды над нулем графика, см	Рас-ход вод, м'/с	Пло-щадь водного сечения, м2	скорость течения, м/с		Ширина реки, м	Глубина, м		Уклон водной поверх­ности, %	Спо-соб измерения расхода
							СРЕД-НЯЯ	Наи-боль-шая		средняя	наиболь­шая
1	2	3	4	6	б	7			10	11	12	13	14
1	9/1	3	ЛДСТ	110	9,00	31,4/23,1	0,39	0,54	30,2	1,04	1.42	—	в 6/18
10	10/1у	2	ЛРДХ	284	66,5	100	0,61	0,70	64,0	1,70	3,14	—	в 9/17
13	12/1у	2	СВ	461	188	291	0,65	0,91	120	2,42	4,92	0,18	в 6/65
17	15/1у	2	СВ	475	196	309	0,63	1,02	122	2,53	5,00	0,20	в 16/73
57	8/х11	3	Заб	108	14,3	30,1	0,48	0,78	30,2	1,00	1,45	—	в 7/29
59	30/х 11	3	ЛДСТ	168	18,8	49,8/46,1	0,41	0,79	35,1	1,42	2,10	—	в 7/39

Частота измерения расходов различна для различных периодов гидрологического режима, кроме того, она неодинакова для рек с различными режимами. Более частые измерения расходов производятся в периоды наибольших их изменений, т. е. в период половодья и паводка. В весеннее половодье обычно производятся 4—5 измерений расхода на подъеме и 5—8 измерений на спаде приблизительно через равные интервалы уровней. В устойчивую межень производят одно измерение через 7—10 суток; при прохождении дождевых паводков рекомендуется делать 1—2 измерения на подъеме и 2—3 измерения на спаде каждого значительного паводка. При устойчивом и длительном ледоставе и плавном изменении уровня воды расходы измеряют через 10—20 суток, а при ледоходе и шугоходе — так часто, как это возможно.

Кривая расходов (рис. 8.5.) строится в прямоугольной системе координат: по оси ординат откладываются уровни воды над нулем графика (Н см), а по оси абсцисс — расход воды (Q м^з/сек).

Зависимость Q=f(H) может выражаться графически в виде одной плавной кривой. В этом случае определенному значению уровня соответствует одно определенное значение расхода воды. Такая зависимость называется однозначной.

Однозначная зависимость охватывает обычно ограниченный период времени. Однако для некоторых рек однозначная зависимость Q=f(H) может сохраняться в течение годового цикла или даже в многолетнем периоде. Однозначная кривая расходов всегда направлена выпуклостью вверх.

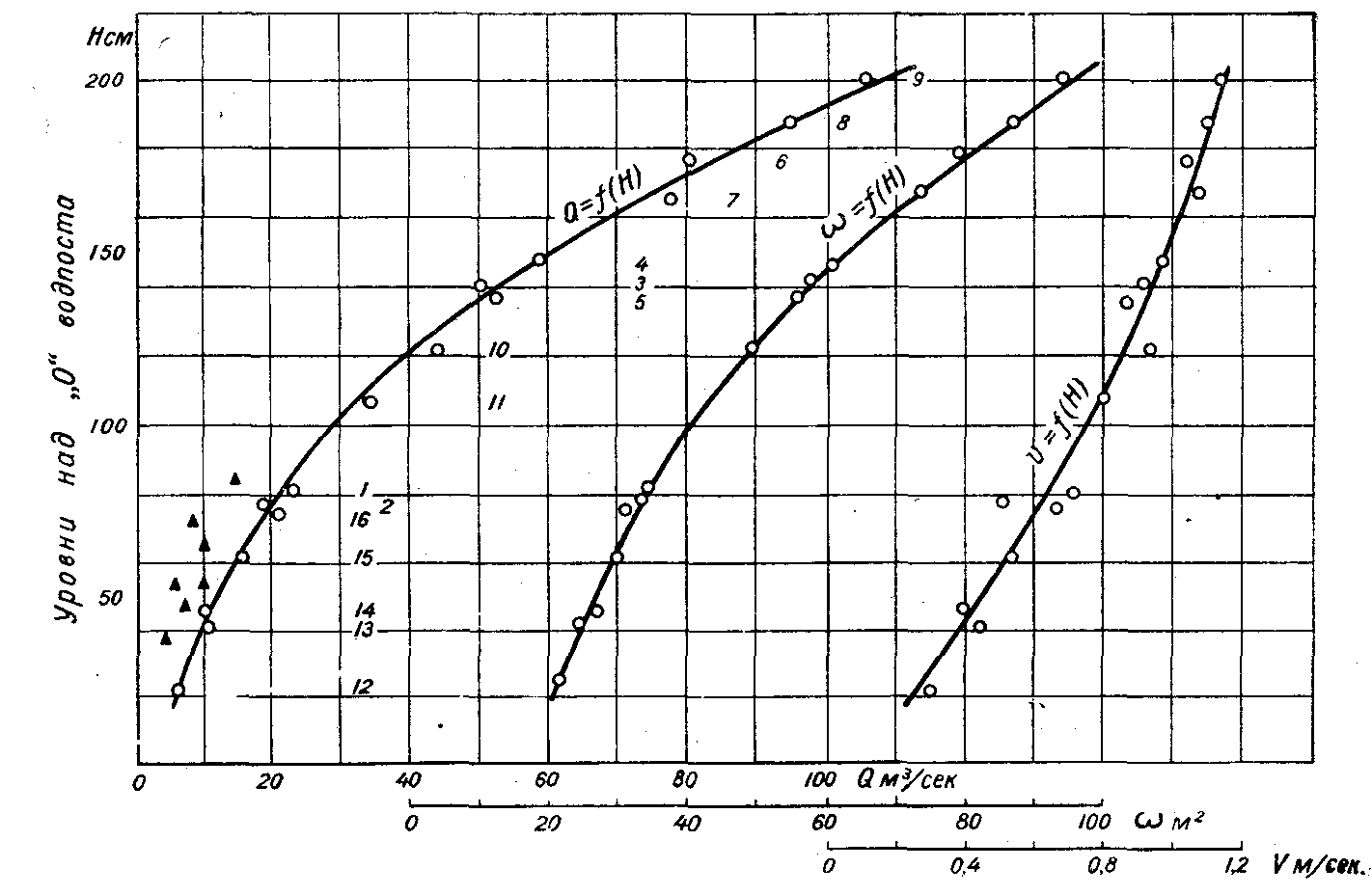
Рис.8.5. Кривые расходов, площадей живого сечения и средних скоростей в зависимости от уровня воды.

Во многих случаях зависимость Q=f(H) приобретает весьма сложный вид, что объясняется влиянием различных факторов, вносящих искажения в эту зависимость. К числу подобных факторов относятся:

1. неустановившееся движение воды;

2. ледяные образования;

3. зарастание русла водной растительностью;

4. неустойчивость русла — размывы и намывы;

5. переменный подпор.

В указанных случаях однозначная зависимость Q=f(H) нарушается, и определение этой зависимости бывает сопряжено с большими трудностями.

Перед тем как приступить к построению кривой расходов, необходимо проанализировать исходные материалы. Расходы, измеренные детальным способом вертушкой, являются наиболее достоверными (вероятная ошибка при благоприятных условиях измерения 3—5%) и служат опорными. Расходы, измеренные вертушкой основным и сокращенным способами, а также измеренные поплавками, менее достоверны (вероятная ошибка 5% и более в зависимости от условий измерений). При анализе исходных материалов обращается внимание на обстановку работ при измерении расходов, так как ветер, малые скорости течения, косоструйность и т. д. могут вызвать погрешности измерений. Определяется уровень, при котором возможен выход воды на пойму. Устанавливается, зарастает ли русло водной растительностью в период вегетации. Выявляется наличие на пойме протоков. Обращается внимание на правильность определения расчетного уровня.

Построение кривой расходов для свободного русла

Для построения кривой расходов в координатной системе (Q, Н) наносятся на миллиметровой бумаге точки измеренных расходов, которые обычно располагаются узкой полосой. Кривая расходов проводится на глаз по середине полосы рассеивания точек расходов, измеренных при свободном состоянии русла (т. е. при отсутствии ледяного покрова и водной растительности). На том же чертеже строится кривая площадей водного сечения w=f(H) и кривая средних скоростей Vcp=f(H). Для построения этих кривых используется та же шкала уровней H по оси ординат, что и для кривой расходов. По оси абсцисс откладываются:

- для кривой площадей - площади водного сечения при соответствующих уровнях воды;

• для кривой средних скоростей - средние скорости течения.

Эти шкалы строятся с некоторым смещением их вправо, как показано на рис.8.5. Данные для построения кривых площадей и средних скоростей течения берутся из таблицы 8.4.

Кривая площадей водного сечения w=f(H) имеет выпуклость кверху. При уровне, соответствующем выходу воды на пойму, кривая площадей становится более пологой. Кривая средних скоростей Vcp=f(Н) обычно имеет выпуклость, обращенную к оси V, а при выходе воды на пойму получает перелом.

Кривые Q =f (Н), w = f (H) и Vср = f (H) связаны между собой равенством Q = w х V, по которому производится увязка кривых.

В таблице 8.5. производится сопоставление расходов для выборочных значений уровня Н (практически это следует делать для всей амплитуды). Расхождение между расходами, вычисленными по произведению Q=w х V и снятыми с кривой, должно быть не более 1 %; если оно больше, то следует в соответствующем интервале исправить кривые.

Таблица 8.5.

Вычисление отклонений от кривой Q =f (Н)

Hсм	w м2	V м/с	Qв=w*V м3с	Qk м3/с с кривой	=QB - QK

Полученная кривая Q=f(H) используется для определения расхода воды по уровню, для чего составляется таблица координат кривой (табл. 8.6.). При составлении таблицы 8.6. с кривой снимаются значения расходов через интервалы уровня 10 см и записывается в графу 2. Прямолинейной интерполяцией между расходами, снятыми с кривой через 10 см, определяется приращение расхода воды на 1 см уровня и записывается в графы 4-12.

Таблица 8.6.

Таблица координат кривой Q=f(H).

При-раще-ние	Н см	0	1	2	3	4	5	6	7	8	9
1	2	3	4	5	6	7	8	9	10	11	12
0	10	20,0	20,5	21,0	21,5	22,0	22,5	23,0	23,5	24,0	24,5
5	20	25,0	25,5	26,0	26,5	27,0	27,5	28,0	28,5	29,0	29,5
5	30	30,0
	40
	50