
- •Лабораторная работа № 1 определение морфометрических характеристик бассейнов рек
- •Лабораторная работа №2 эксперементальное определение величин уравнения водного баланса
- •Лабораторная работа № 3 движение подземных вод
- •Лабораторная работа № 5 расчет испарения с водной поверхности при отсутствии наблюдений
- •Лабораторная работа № 8 вычисление ежедневных расходов воды по наблюдениям на водомерных постах
- •Вычисление расхода воды
- •Вычисление стока при ледовых явлениях
- •Интерполяция между измеренными расходами
Лабораторная работа № 3 движение подземных вод
Цель работы: используя законы движения подземных вод, построить кривые депрессии грунтового потока на некотором расстоянии от реки (задание № 1) и через плотину трапецеидального сечения (задание № 2).
Исходные данные:
Задание № 1:
-схема расположения уровня воды в реке и грунтовом потоке, положение водоупора выдается индивидуально.
-прямой уклон
грунтового потока
![]() =0,02,
обратный уклон грунтового потока 0,01,
глубина в начале потока
=0,02,
обратный уклон грунтового потока 0,01,
глубина в начале потока
![]() =2,2м,
в конце потока
=2,2м,
в конце потока
![]() =4м,
- фильтрационный расход
=0,04
см2/с,
=4м,
- фильтрационный расход
=0,04
см2/с,
-коэффициент фильтрации =0,01 см/с.
Задание № 2:
высота плотины
 =11м,
глубина в верхнем бьефе
=11м,
глубина в верхнем бьефе
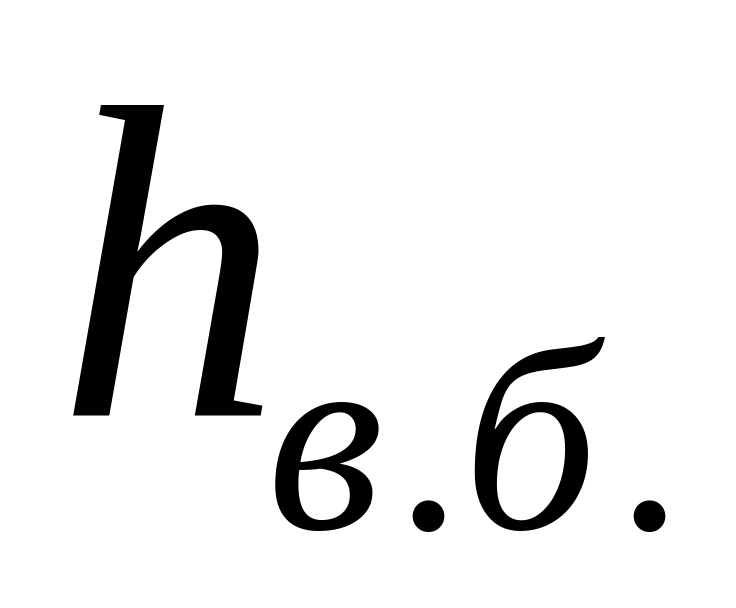 =10м,
в нижнем бьефе
=10м,
в нижнем бьефе
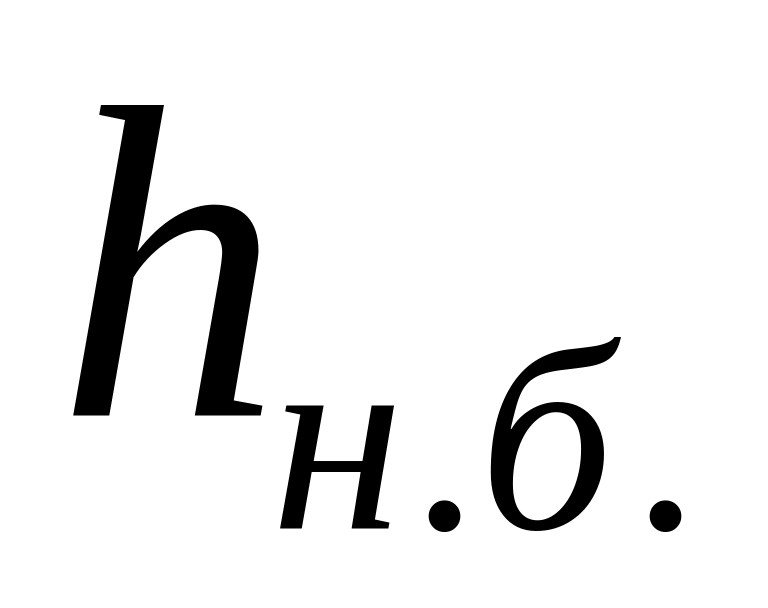 2м,
2м,
ширина плотины по верху =8м,
-заложение откосов
![]() =3,
=3,
![]() =2,
=2,
-коэффициент фильтрации =0,0004 см/с.
Определить:
Для упражнения №1 - координаты кривой депрессии с выходом в естественное речное русло;
Для упражнения №2 - координаты кривой депрессии фильтрационного потока через плотину.
Задание №1. Построение кривой депрессии грунтового потока на некотором расстоянии от реки.
Основной закон ламинарной фильтрации (закон Дарси) может быть записан так [8] :
![]() (3.1)
(3.1)
или
![]() (3.2)
(3.2)
где V — скорость фильтрации;
![]() — фильтрационный
расход;
— фильтрационный
расход;
— гидравлический уклон;
![]() — полная площадь
поперечного сечения потока, включая и
площадь, занятую твердыми частицами
грунта;
— полная площадь
поперечного сечения потока, включая и
площадь, занятую твердыми частицами
грунта;
—коэффициент фильтрации, примерные значения которого для разных грунтов следующие, см/с:
Наименование грунта |
Коэффициент фильтрации |
Гравий с размером зерен 4 — 7 мм |
3,5 |
Гравий с размером зерен 2 мм |
3 |
Песок чистый |
1,0—0,01 |
Песчаный грунт с примесью глины |
0,01—0,005 |
Песчано-глинистый грунт |
0,005—0,0001 |
Глины |
10 -4—10-7 |
Глина плотная (утрамбованная) |
10-7—10-10 |
При безнапорной фильтрации и равномерном движении грунтовых вод скорость и расход определяются по формулам:
![]() (3.3)
(3.3)
или
![]() (3.4)
(3.4)
где — уклон водоупорного подстилающего слоя.
Для прямоугольного сечения грунтового потока расход определяется по формуле:
![]() (3.5)
(3.5)
или
![]() (3.6)
(3.6)
где
![]() — глубина потока при равномерном
движении;
— глубина потока при равномерном
движении;
— ширина потока;
— удельный расход.
При плавно изменяющемся неравномерном движении грунтовых вод для широких потоков расчетные формулы имеют следующий вид (в зависимости от уклона подстилающего слоя) [8]:
1) при уклоне == 0 (рис. 3.1):
![]()
![]() (3.8.)
(3.8.)
где
![]() —расстояние
между сечениями потока с глубинами
и
;
—расстояние
между сечениями потока с глубинами
и
;
2) при прямом уклоне ( > 0, рис. 3.2):
а) для кривой подпора
![]() (3.9.)
(3.9.)
б) для кривой спада
![]() (3.10.)
(3.10.)
где
![]() и
и
![]() .
.
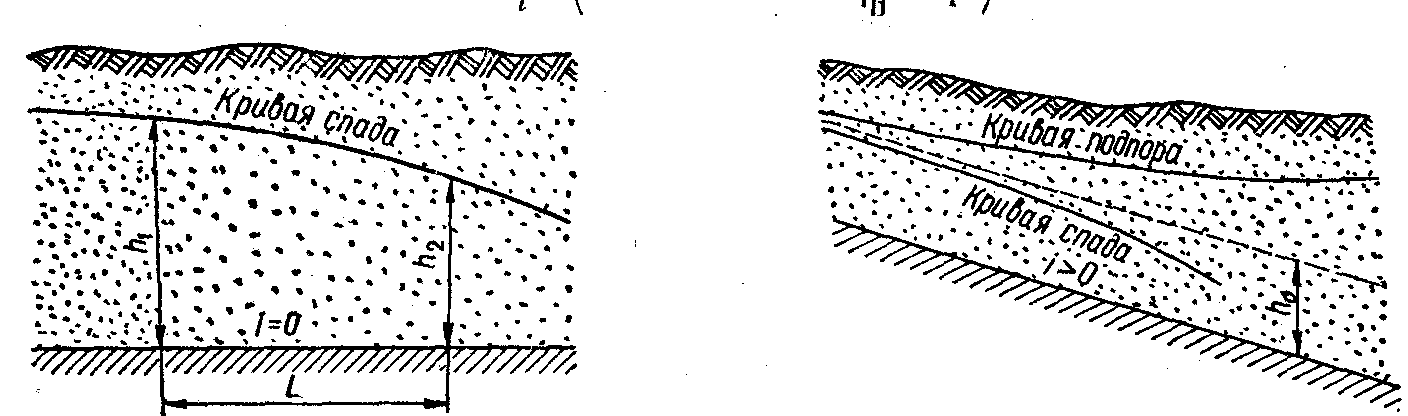
Рис. 3.1. Рис. 3.2.
3) при обратном уклоне ( < 0, рис. 3.3):
![]() (3.11.)
(3.11.)
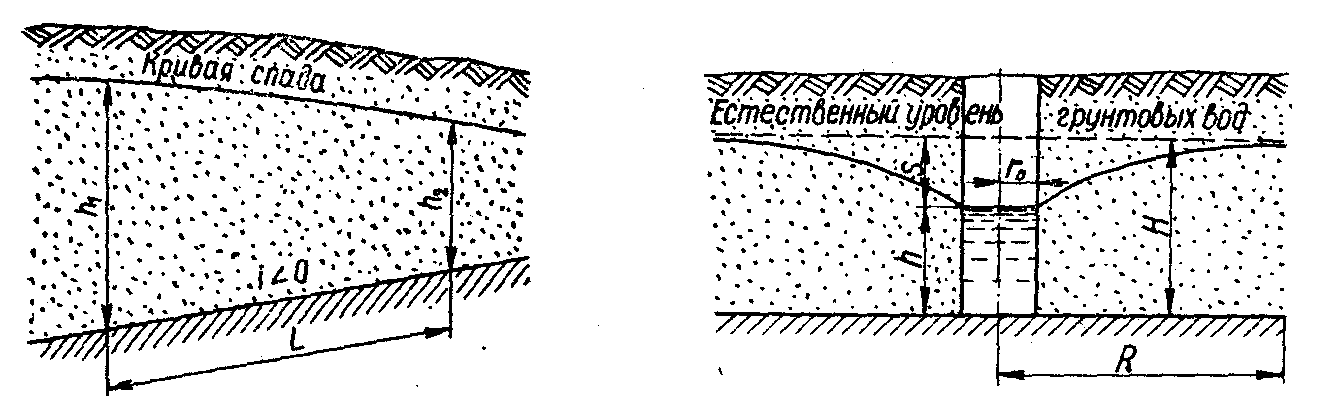
Рис.3.3. Рис.3.4.
Порядок выполнения работы
По формуле (3.6.)
устанавливается глубина при равномерном
движении
.
Имея значения глубин в начале и конце
потока и глубину равномерного движения,
строим кривую подпора по уравнению,
выбор которого зависит от знака уклона:
к реке - положительный уклон, от реки -
отрицательный. Для этого на масштабной
схеме откладывают произвольное расстояние
![]() .
По формуле (3.9.) или (3.11.) определяют
глубину потока для этого расстояния.
Задаваясь значениями
.
По формуле (3.9.) или (3.11.) определяют
глубину потока для этого расстояния.
Задаваясь значениями
![]() ,
которых должно быть не менее 3-х, строят
кривую депрессии.
,
которых должно быть не менее 3-х, строят
кривую депрессии.
Задание № 2. Построение кривой депрессии фильтрационного потока
через плотину.
Решение задачи о фильтрации воды через плотину - сводится к определению фильтрационного расхода и построению кривой депрессии. Форма депрессионной кривой и фильтрационный расход могут быть определены методом Н. Н. Павловского [8] или методами других ученых. Решают задачу подбором или графически.
Расчет производится по способу, рекомендованному М. Д. Чертоусовым, при следующих обозначениях (рис. 3.5)
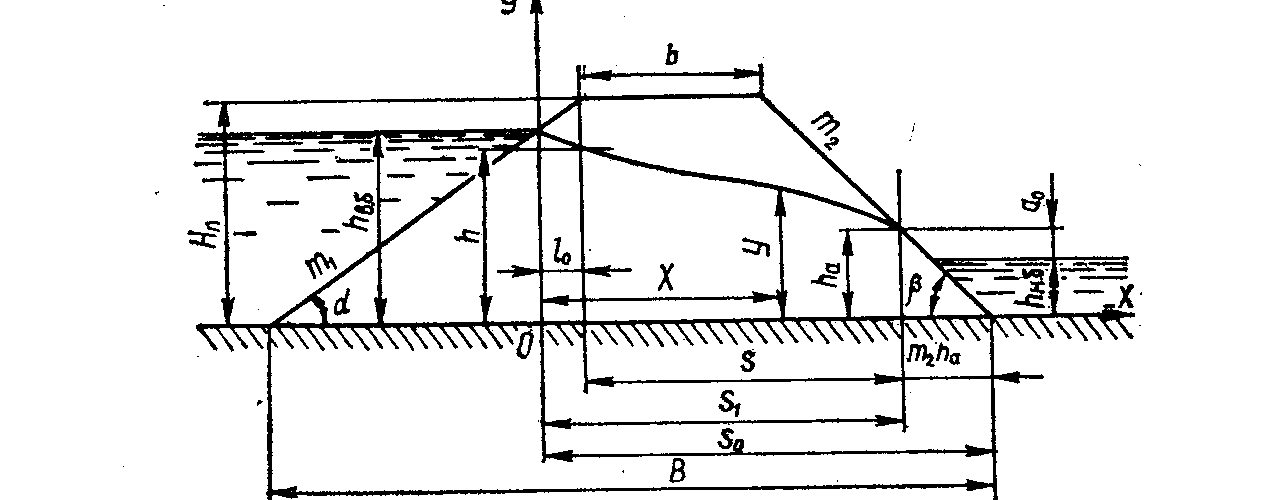
Рис.3.5.
— глубина воды в верхнем бьефе;
— глубина воды в нижнем бьефе;
— высота плотины;
![]() — превышение точки
выклинивания кривой депрессии на низовой
откос над уровнем воды в нижнем бьефе;
— превышение точки
выклинивания кривой депрессии на низовой
откос над уровнем воды в нижнем бьефе;
— ширина плотины поверху;
В— ширина плотины понизу;
![]() и
и
![]() — коэффициенты заложения верхнего и
низового откосов плотины.
— коэффициенты заложения верхнего и
низового откосов плотины.
Понижение кривой
депрессии в теле плотины определяется
величинами
,
,
![]() ,
,
![]() ,
,
![]() .
.
Расчетные зависимости имеют следующий вид:
![]()
 (3.12)
(3.12)
где:
![]() (3.13)
(3.13)
![]() (3.14)
(3.14)
![]() (3.15)
(3.15)
![]() (3.16)
(3.16)
![]() (3.17)
(3.17)
Если глубина воды
в нижнем бьефе
равна нулю, то
=
и множитель
![]() по формуле (3.14) обращается в единицу.
по формуле (3.14) обращается в единицу.
Коэффициент
![]() в зависимости от
принимает значения,
определяемые
по формуле:
в зависимости от
принимает значения,
определяемые
по формуле:
![]() ,
,
где
![]()
m1 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
ε |
2,000 |
1,634 |
1,459 |
1,358 |
1,293 |
1,214 |
Систему уравнений
(3.12) можно решать построением графиков
функций
![]() и
и
![]() по
зависимостям:
по
зависимостям:
=![]() (3.18.)
(3.18.)
и
![]() (3.19.)
(3.19.)
где
![]() (3.20.)
(3.20.)
Для упрощения
решения задачи можно принимать
![]() ;
при этом
определяется зависимостью (3.18), а функция
по формуле:
;
при этом
определяется зависимостью (3.18), а функция
по формуле:
![]() (3.21.)
(3.21.)
Кривую депрессии в средней части профиля плотины строят по уравнению:
![]() (3.22.)
(3.22.)
при уравнение 3.22) принимает вид
![]() (3.23.)
(3.23.)
Порядок выполнения работы
Чтобы построить
кривую депрессии и определить
фильтрационный расход на 1 м длины
однородной земляной плотины, расположенной
на горизонтальном водоупоре, если
= 11 м;
= 10 м;
= 8 м;
=3,
![]() ,
,
![]() 0,0004
см/с,
0,0004
см/с,
![]() 2м,
необходимо:
2м,
необходимо:
Определить постоянные величины, входящие в основные уравнения. Коэффициент при
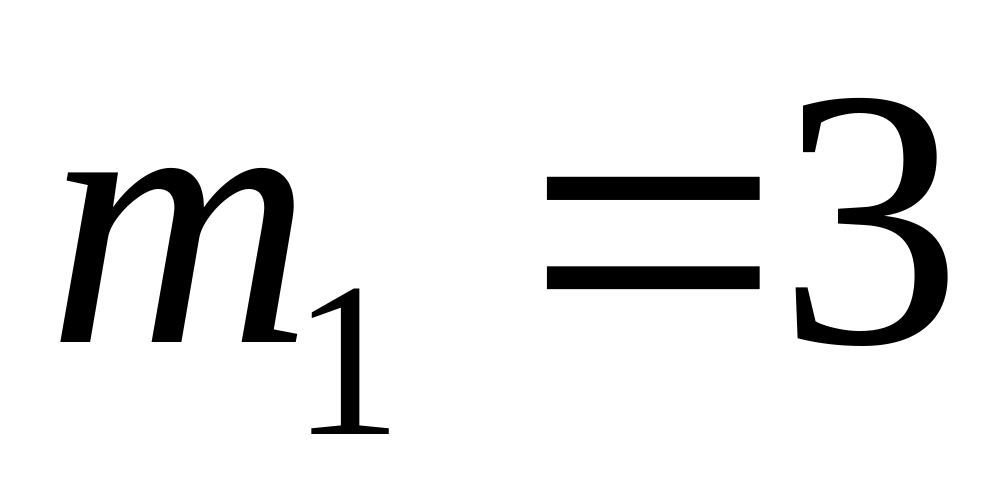 равен 1,293.
равен 1,293.
Коэффициенту
соответствует
![]() и
и
![]() .
.
Ширина плотины
понизу
![]()
Значение
2. Задаваясь произвольным значением определяем и :
Параметры
и
определяем по формулам (3.13.), (3.14.),
![]() по
формуле (3.20).
по
формуле (3.20).
Значения , определим по зависимостям (3.18.) и (3.21.)
Результаты расчета сводим в таблицу 3.6.
Таблица 3.6.
-
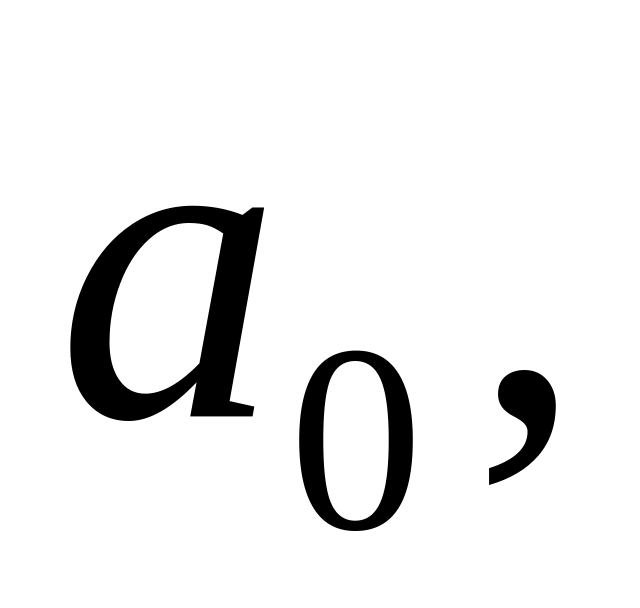 м
м, м
, м
,м
По полученным данным строим графики функций и , как показано на рис.3.6.
По графику определяем
и
,
равную величине
![]() .
.
Глубину фильтрационного потока определяем по первому уравнению системы (3.12.):

Расстояние
![]()
Кривую депрессии в средней части строим по уравнению (3.22.)
Пример построения кривой депрессии приведен на рис.3.7.
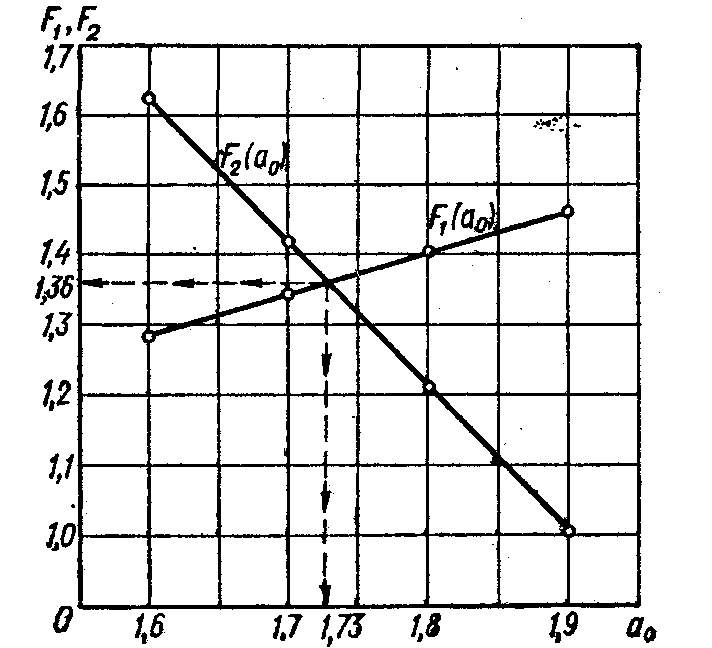
Рис.3.6. Графики функций и
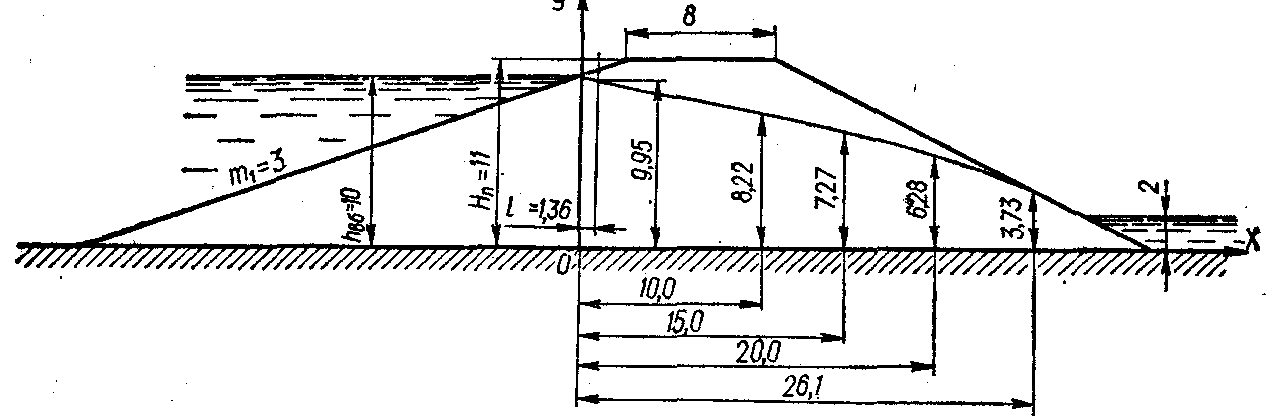
Рис. 3.7. Построение кривой депрессии
