5.4. Потери в трансформаторах

Под потерями в трансформаторе понимается мощность Рс, затрачиваемая на перемагничивание и вихревые токи в сердечнике, и мощность Рm затрачиваемая на нагрев обмоток.

В конечном счете мощность потерь выделяется в виде тепла, которое должно быть рассеяно в окружающую среду.

Потери на вихревые токи зависят от удельного сопротивления материала сердечника и от частоты магнитного поля. Чтобы уменьшить эту составляющую потерь, для сердечников применяют специальные трансформаторные стали с большим удельным сопротивлением. Кроме того сердечники изготовляют из тонких листов, изолированных друг от друга. Чем выше частота тока, тем больше потери на вихревые токи, поэтому сердечники трансформаторов, работающих на высоких частотах, делают из более тонкого металла.

Потери па перемагничивание (гистерезис) зависят от максимальной индукции в сердечнике: чем больше индукция, тем больше площадь петли гистерезиса и тем больше потери. Обычно при расчетах потери на перемагничивание и вихревые токи не разделяют и свойства материала оценивают удельными потерями  Рс.уд, т.е.потерями, отнесенными к 1 кг материала:

Рс.уд = аВm2,

( 5.14)

где а – эмпирический коэффициент; а = 2…3.

Потери в сердечнике зависят от массы сердечника Gс:

Рс = Рс.уд Gс.

(5.15)

Н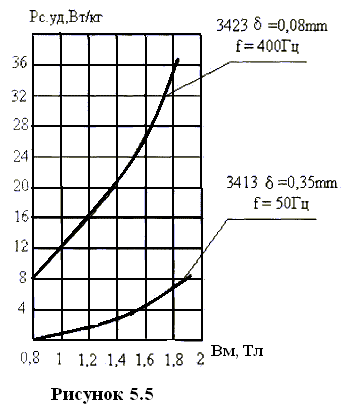 а рисунке 5.5 представлены эмпирические зависимости удельных потерь от индукции.

Величину индукции можно определить из (5.5), приняв в нем ЭДС индукции равной подводимому напряжениюU₁;

Bm = 103

(5.16)

Из (5.16) следует, что увеличивая число витков первичной обмотки трансформатора и площадь сечения сердечника, можно снизить индукцию Bт, а следовательно, потери в сердечнике.

Потери на нагрев обмоток определяются соотношением

Рм = I12R1 + I22R2 = ,

( 5.17)

где ρ – удельное сопротивление провода; l₁ и l₂ – длина провода первичной и вторичной обмоток, соответственно; Sп1 и Sп2 - площадь поперечного сечения провода первичной и вторичной обмоток, соответственно.

Длина провода

l1 = lCP1w1, l2 = lCP2w2,

(5.18)

где  lср – средняя длина витка, зависящая от типа сердечника и расположения на нем обмотки.

Площадь поперечного сечения провода можно выразить через площадь окна Sо, занимаемую медью соответствующей обмотки:

Sп1 = , Sп2 = .

(5.19)

Подставляя  l₁ ,  l₂ , Sп1  и Sп2 в  (5.17), легко установить, что потери в меди пропорциональны квадрату числа витков, а число витков, как это следует из (5.16), обратно пропорционально индукции Вт. Следовательно,

Рм ~

( 5.20)

И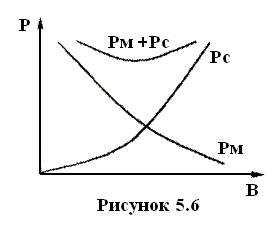 з того, что с ростом индукции Вт потери в сердечнике возрастают (5.14), а потери в меди уменьшаются (5.20), следует, что существует такое значение индукции, при котором суммарные потери в трансформаторе минимальны (рисунок 5.6).

 

Это значение зависит от свойств материала сердечника, частоты подводимого напряжения и ряда других причин (мощности трансформатора, размещения на нем обмоток и т. д.). В таблице 5.1 приведены полученные экспериментально оптимальные значения индукции, которыми руководствуются при расчете трансформаторов.

Таблица 5.1

Материал магнитопровода	f, Гц	Вт, Тл, при мощности Р2 , Вт
		4-100	100-250	250-300	300-600	600-1000
Э424, толщина 0,08…0,15 мм	400	1,5	1,4	1,3	1,2	1,1
Э413, толщина 0,35 мм	50	1,55	1,55	1,55	1,55	1,55