1.2.5Итерационный алгоритм Витерби с мягким решением
Рассмотрим снова турбо кодер, показанный в рис. 2, блок-схема итерационного мягкого вывода Viterbi алгоритма изображена на рис. 3. Первый декодер Витерби с мягким выходом (ABMP) выносит мягкое решение 1(bt), где t - текущий момент времени. Мягкий вывод перемежается и используется вторым декодером ABMP. Второй ABMP декодер также выносит мягкое решение 2(bt) которое используется на следующей итерации в первом ABMP декодером.
Мягкое решение на выходе каждого декодера ABMP выносится в соответствии с выражением (33) так
(36)
В итерационном декодировании априорная вероятность bt вообще отличается 0.5, поскольку предыдущая ступень декодирования обеспечивает улучшенную оценку относительно двоичного симметричного источника. Следовательно вес пути в уравнении (36) для первого ABMP декодера может быть вычислен, из уравнений (24), (26) и (25) как
(37)
где
обеспечивается предыдущей ступенью
декодирования. Как и в алгоритме МАВ,
мягкая выходная информация (bt)
из ABMP декодера разлагается в две части,
собственная информация i(bt)
и примесная информация e(bt).
Примесная информация e(bt)
может использоваться как априорная
информация для следующей ступени,
декодирующей после перемежения или
деперемежения. Обозначим 1(bt)
выход первого декодера. Присущая
информация - 1i(bt)
и примесная информация - 1e(bt).
Объединяя уравнения (33) и (37) состояние
на выходе декодера ABMP может быть выражено
как
(38)
где
(39)
и
(40)
Так, примесная информация e(bt) может быть получена из (38) и (39) как
(
41)
где
– логарифм отношения априорных
вероятностей приравнивается к
деперемежённой примесной информации
второго декодера при итерационном
декодировании. Обозначим
деперемежённую примесную информацию
от второго декодера. Затем выражение
(40) преобразуется в
(
42)
Аналогично, обозначим 2(bt) выход второго декодера с присущей информацией и примесной информацией 2i(bt) и 2e(bt) соответственно. Затем как в (4.40) преобразуем
(43)
где
перемежённая примесная информация от
первого декодера.
1.2.6Заключение по итерационному алгоритму abmp
Инициализация
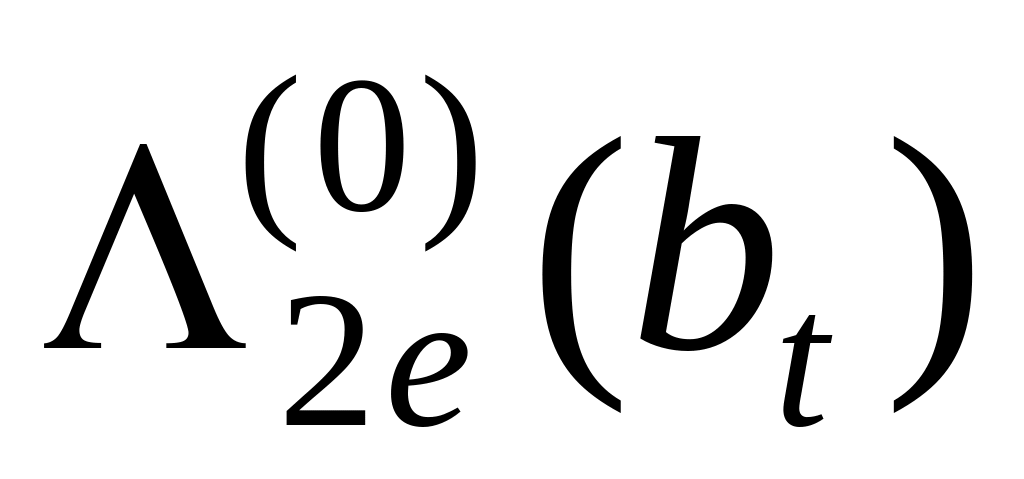=0.Для итерации r= 1, 2, ..., I , где I – полное количество итераций, вычисляется
и
в соответствии с выражениями (32) и (36).После I итераций выносится жёсткое решение о значении bt на основании
1.2.7Сравнение характеристик мав и abmp
Вероятность ошибки бита для турбо кода c относительной скоростью 1/3 и 16 состояниями для алгоритмов декодирования МАВ и ABMP с тем же самым числом итераций 18 и размера перемежителя 4096 символов. Результаты декодирования по ABMP выражаются в снижении Энергетического выигрыша кодирования (ЭВК) на 0.7dB при вероятности ошибки бита 10-5 но при этом требуется существенно меньшее количество времени. По результатам моделирования декодер ABMP работает вдвое быстрее декодера MAВ.
1.2.8Заключение
Итерационный MAВ алгоритм и двунаправленный алгоритм Витерби с мягким решением представлены и применяются для декодирования турбо кодов. Алгоритм МАВ - в вычислительном отношении намного сложнее чем алгоритм Витерби. В алгоритме МАВ используются операции умножения и возведения в степень, в то время как в алгоритме Витерби это просто, сложение, сравнение и выбор.
В качестве примера, эти алгоритмы применяются к декодированию турбо кодов, и их характеристики сравнивается в Гауссовом канале. Итерационный МАВ алгоритм имеет преимущество в ЭВК на Гауссовом канале относительно итерационного ABMP на 0.5dB при вероятности ошибки бита 10-4.