4.2.2. Примеры расчетов простых трубопроводов

Задача № 1. Задано: расход жидкости (Q), ее свойства (ν), размеры трубопровода (l,d) и шероховатость его стенок.

Необходимо найти требуемый напор.

1. По известным значениям Q, D,ν рассчитываем критерий Рейнольдса и определяют режим движения жидкости.

2. При ламинарном режиме напор определяют по формуле

_. (4.31)

- приведенная длина трубопровода. Эквивалентные длины l местных сопротивлений при ламинарном режиме движения жидкости в трубопроводе существенно зависят от числа Рейнольдса .

При турбулентном режиме движения жидкости напор определяем по формулам (4.15) – для короткого трубопровода и (4.21) - для длинного с преобладающими потерями на трение, в которых по известным Re, d и выбираем соответствующие величины λ, ζ и l_э .

Задача № 2. Задано: располагаемый напор H, размеры трубопровода l и d, шероховатость его стенок ∆ и свойства жидкости (ν).

Необходимо найти расход жидкости Q.

Определяем режим движения жидкости сравнением напора Н с его критическим значением

.

Если H < H_кр, то режим движения жидкости ламинарный и если H > H_кр - турбулентный.

Далее задача решается методом последовательных приближений. При ламинарном режиме расход определяют по формуле (4.31), в которой последовательными приближениями уточняют выбранные значения эквивалентных длин местных сопротивлений и приведенную длину трубопровода L.

При турбулентном режиме в качестве первого приближения принимаем квадратичную область сопротивления, в которой по известным значениям d и ∆ определяют значения λ и ζ, позволяющие найти из формул (4.15) или (4.21) расход Q. Расчет Re по найденному значению Q дает возможность уточнить значения коэффициентов сопротивлений и определить расход во втором приближении, что, как правило, оказывается достаточным.

Для технически гладких труб в качестве первого приближения следует использовать для нахождения расхода формулу Блазиуса, в соответствии с которой

(4.32)

При этом следует предварительно оценить приведенную длину трубопровода L с учетом имеющихся местных сопротивлений.

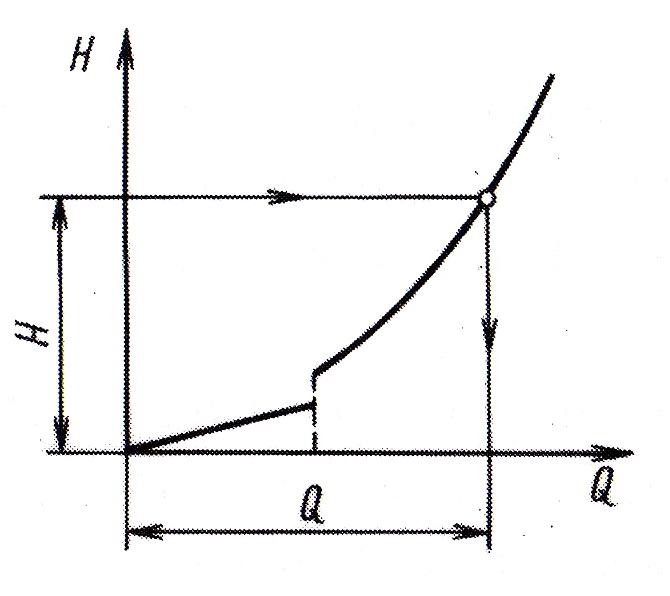
Целесообразно проводить и графическое решение задачи, основанное на построении характеристики трубопровода – зависимости требуемого перепада гидростатических напоров (Н) от расхода Q (рис. 4.7). Характеристика строится по уравнениям зависимости между H и Q, приведенным выше для ламинарного и турбулентного режимов течения жидкости, с учетом зависимости λ и ζ от Re, то есть от расхода Q.

При этом учитываем, что при турбулентном режиме течения в трубопроводе значения ζ в большинстве случаев очень слабо зависят от критерия Рейнольдса и в расчетах их можно считать постоянными.

Для длинного трубопровода указанную характеристику можно рассматривать как зависимость суммарных потерь напора в трубопроводе от расхода.

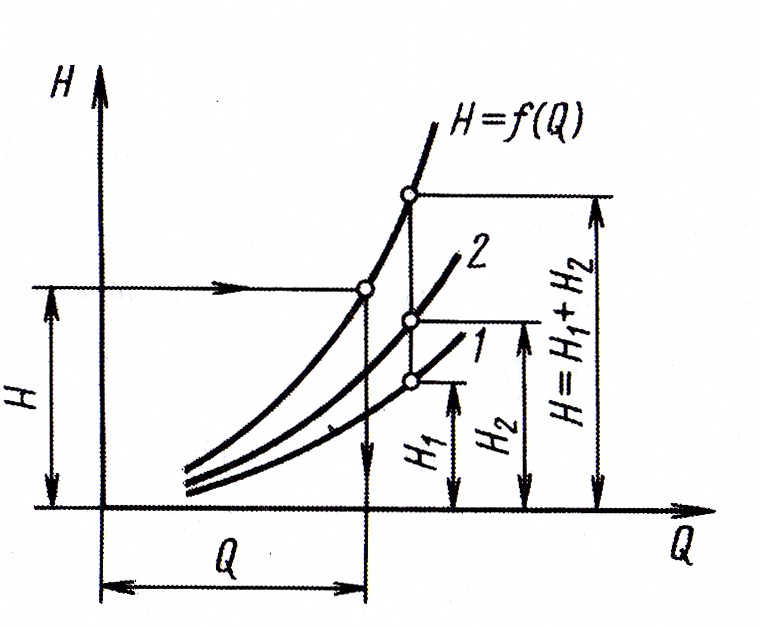
Графический способ, исключающий необходимость в последовательных приближениях, особенно удобен для трубопровода, состоящего из нескольких участков различного диаметра, характеристика которого позволяет найти расход Q по известному значению напора H, получается суммированием ординат характеристик отдельных участков (рис. 4.8).

Рис. 4.7. Зависимость напора в трубопроводе от расхода жидкости

Рис. 4.8. Зависимость напора в трубопроводах различного диаметра от расхода жидкости

Задача № 3. Задано: располагаемый напор H, расход Q, длина трубопровода l, шероховатость его стенок ∆ и свойства жидкости(ν).

Необходимо найти диаметр трубопровода d.

Определяем режим движения жидкости в трубопроводе путем сравнения напора Н с его критическим значением.

(4.33)

Если H < H_кр , то режим движения ламинарный; Если H > H_кр - турбулентный.

Задачу, как правило, решают графическим способом – построением зависимости требуемого напора Н от диаметра трубопровода d при заданном расходе Q.

Задавая различные значения d, для каждого из которых определяются величины ζ и l с учетом области сопротивления, вычисляем соответствующие значения напора Н из приведенных выше соотношений между H и Q.

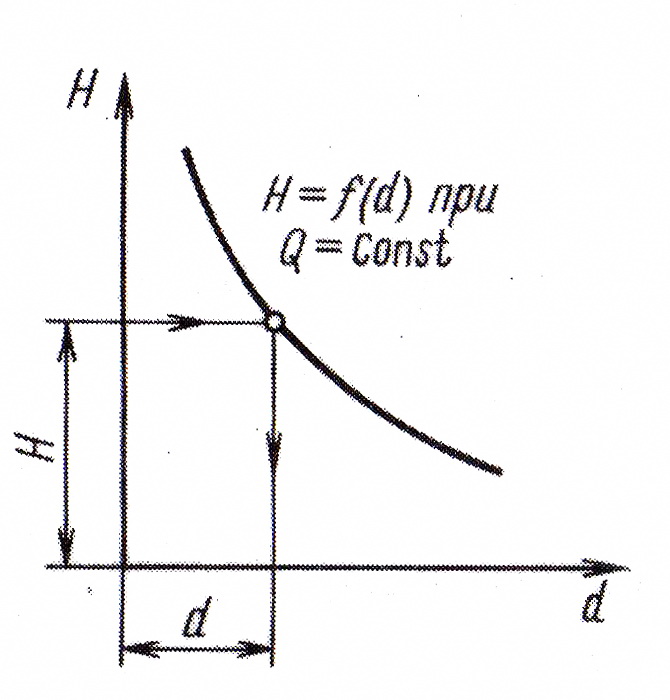
Результаты расчетов представляют в графической форме H = f(d) и по полученному графику по заданному значению Н определяют d и далее уточняют необходимую величину Н при выборе ближайшего большего стандартного диаметра (рис. 4.9).

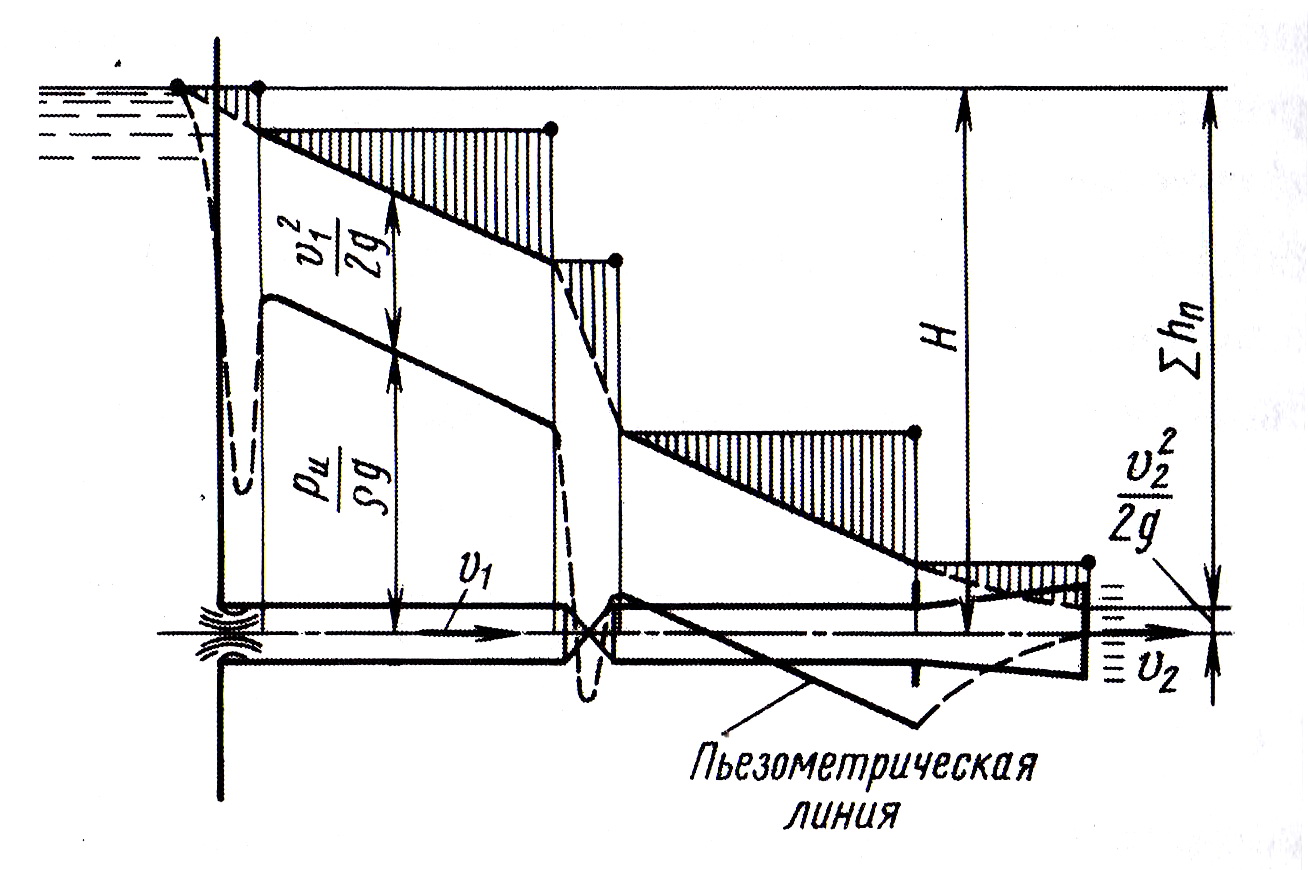
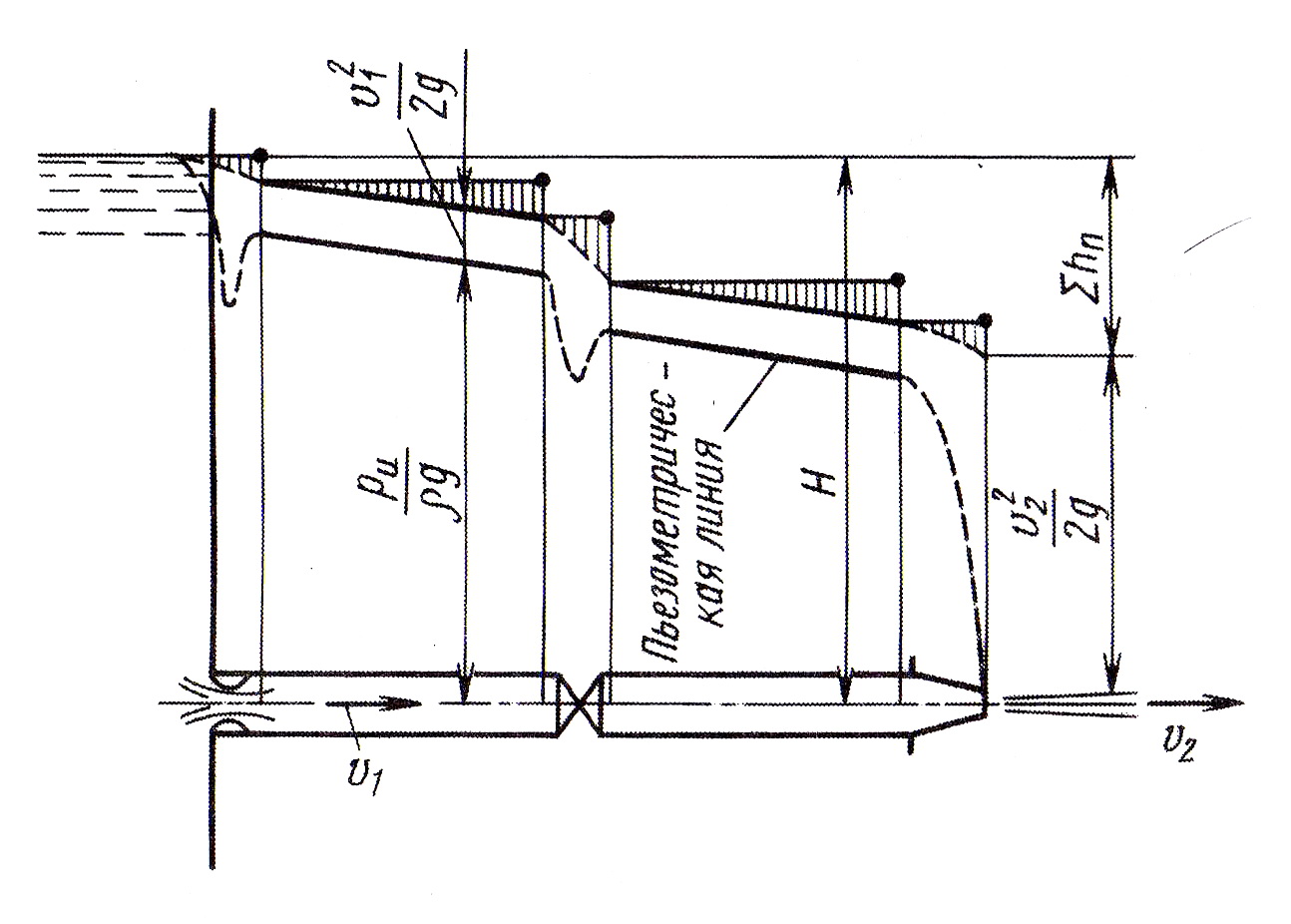
В качестве примера расчета короткого трубопровода определим скорость истечения и расход для трубопровода длиной l и диаметром d при заданном напоре H (рис. 4.10) и для той же трубы с присоединенным к ней сходящимся или расходящимся насадком (рис. 4.11 и 4.12). Режим движения жидкости в трубопроводе – турбулентный.

Рис. 4.9. Зависимость напора трубопровода от его диаметра

Рис. 4.10. Зависимость скорости истечения и расхода жидкости от потерь давления в трубопроводе

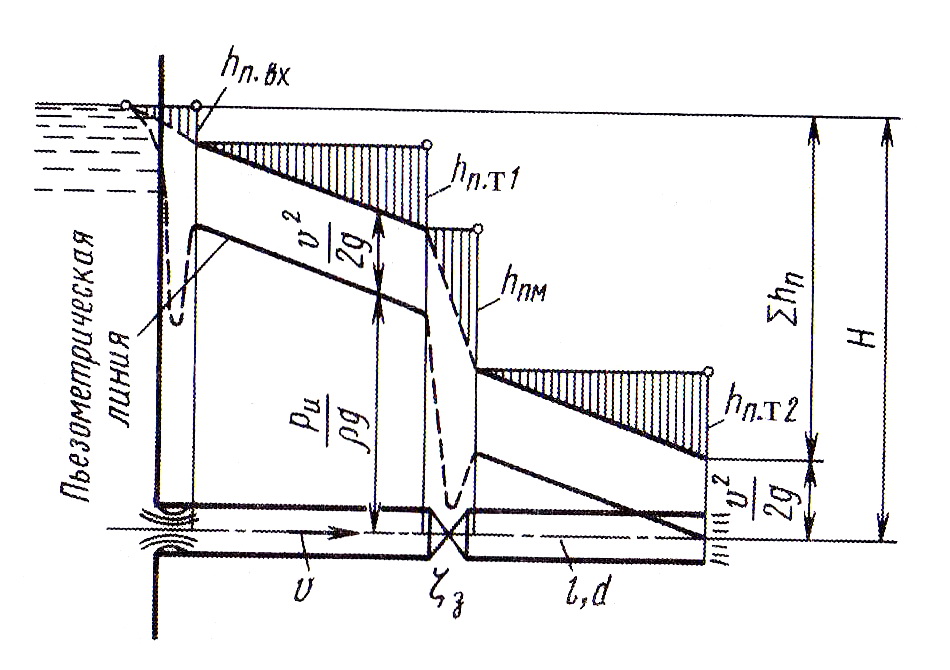
Рис. 4.11. Зависимость скорости истечения и расхода жидкости от потерь давления в трубопроводе со сходящимся насадком

Рис. 4.12. Зависимость скорости истечения и расхода жидкости от потерь давления в трубопроводе с расходящимся насадком

Для трубы без насадка получим

,

откуда получим выражение для скорости истечения

и расхода

,

где

; μ =φ .

Значения коэффициентов местных сопротивлений (входа ζ_вх и вентиля ζ_з) и коэффициента сопротивления трения λ в первом приближении определим в предположении, что в трубопроводе реализуется квадратичная область сопротивления.

Для трубопровода с насадком выходной площадью S₂ и коэффициентом сопротивления ζ_н получим

,

откуда скорость истечения и расход ,

где ;

μ = φ - (при отсутствии сжатия струи на выходе из насадка).

Сравнение формул для коэффициента скорости показывает, что присоединение сходящегося насадка (S₂ < S₁ ), коэффициент сопротивления которого всегда представляет малую величину, увеличивает скорость истечения (W₂ > W₁). Следовательно, что при расчете трубопровода с таким насадком нельзя пренебрегать скоростным напором выхода даже при большой относительной длине l/d трубопровода.

Присоединение расходящегося насадка (S₂ > S₁) уменьшает скорость истечения (W₂ < W₁).

Для выяснения характера изменения расхода жидкости находим скорость ее течения в трубопроводе

Присоединение сходящегося насадка уменьшает скорость в трубопроводе (W₁ < W₂ ) и, следовательно расход Q (W₁→0 при S₂→0). Для расходящегося насадка W₁ > W₂ и расход увеличивается.

Такие изменения расхода объясняются тем, что в концевом сечении трубопровода перед сходящимся насадком возникает избыточное давление, а перед расходящимся – вакуум.