Razdel4

Шаг 4. Найти показатели возможности процесса по индексам:

• возможности технологического процесса, характеризующего потенциальную возможность процесса удовлетворять технический допуск без учета положения среднего значения (применяется для стабильных по разбросу процессов (для процессов в состоянии А и Б)).

, (1)

где - соответственно верхнее и нижнее предельно допустимое значение контролируемого параметра.

• воспроизводимости процесса, оценивающего возможность удовлетворять технический допуск с учетом фактического положения среднего значения и применяемый для стабильных по разбросу и настройке процессов (для процессов в состоянии А)

или (2)

Шаг 5. По известным значениям и оценить возможности процесса путем определения интервала, в котором находится ожидаемый уровень несоответствий (табл. 1), причем:

- по значению определяют минимально возможное значение ожидаемого уровня несоответствий, которые могут быть достигнуты при настройке на центр поля допуска;

- по значению определяют максимально возможное значение ожидаемого уровня несоответствий, если настройка процесса будет оставаться без изменений.

Таблица 1 – Связь индексов и стабильных процессов

с ожидаемым уровнем несоответствий

Значение или	Уровень несоответствий в изделии РЭА		Значение или	Уровень несоответствий в изделии РЭА
	В процентах несоответствующих единиц, %	В числе несоответствующих единиц на миллион изделий		В процентах несоответствующих единиц, %	В числе несоответствующих единиц на миллион изделий
0,33	32,2	322000	1,00	0,27	2700
0,37	26,7	267000	1,06	0,15	1500
0,55	9,9	99000	1,10	0,097	970
0,62	6,3	63000	1,14	0,063	630
0,69	3,8	38000	1,18	0,04	400
0,75	2,4	24000	1,22	0,025	250
0,81	1,5	15000	1,26	0,016	160
0,86	0,99	9900	1,30	0,0096	96
0,91	0,64	6400	1,33	0,0066	66
0,96	0,40	4000

Нетрудно заметить, что при возможности технологического процесса неприемлемы; при - процесс находится на грани требуемых возможностей. На практике приемлемым значением является , т.к. всегда есть некоторые вариации в выборках, и нет процессов, которые всегда находятся в статистическом управляемом состоянии.

Пример. При оценке возможностей технологического процесса получены следующие значения индексов и . Оценить ожидаемый уровень несоответствий.

Используя табл.1 , ожидаемый уровень несоответствий будет находиться в интервале от 1,5% до 3,8%, а число несоответствующих единиц продукции на миллион изделий – от 15000 до 38000.

При высоких значениях возможен выход ряда значений за установленные пределы, поэтому важно оценить расстояние между средним процесса и ближайшим предельно допустимым значением, т.е. рассчитать критический индекс возможности процесса

, или

где - среднее процесса, - один из пределов поля допуска.

Оптимальным значением считается 1,33. Уменьшение (что соответствует перемещению кривой от нижней границы к верхней) повышает вероятность возникновения брака в сторону увеличения размера выше допустимого. Увеличение (перемещение кривой от границы верхней границы к нижней) повышает вероятность возникновения брака в сторону уменьшения размера ниже допустимого.

Шаг 6. Если процесс не стабилен, устранить влияние особых причин и оценить возможности технологического процесса в соответствии с шагами 3 и 4.

Шаг 7. Если устранение влияния особых причин невозможно, то определить возможный вариант состояния процесса:

- процесс нестабилен только по положению среднего арифметического (наличие особых признаков на -карте и/или -карте) (рис. 4, состояние Б) – перейти к шагу 8;

- процесс нестабилен, что подтверждается наличием признаков особых причин на -карте и/или -карте, при этом нельзя оценивать точность настройки по -карте и/или -карте (рис. 4, состояние В) – перейти к шагу 12.

Шаг 8. Рассчитать значение собственной изменчивости процесса по формулам или .

Шаг 9. Найти полную изменчивость процесса по формуле

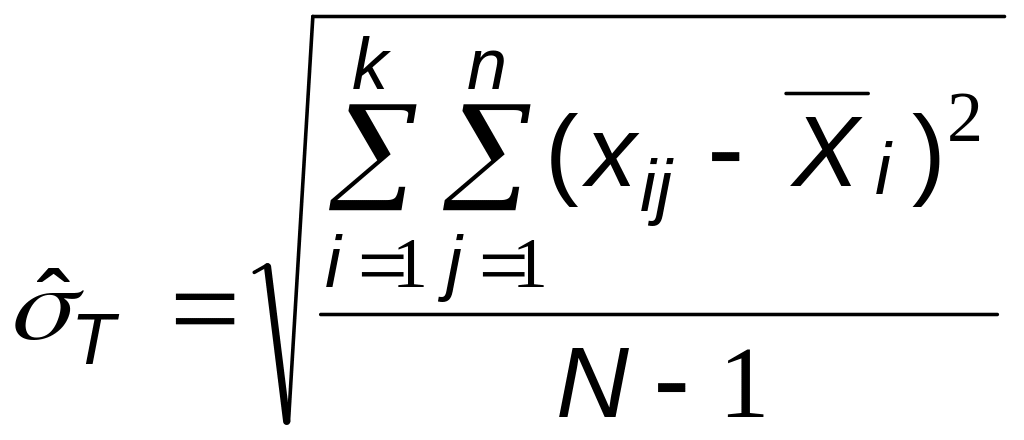, (3)

где - суммарный объем данных во всех выборках объемом ; ‑ возможное значение контролируемого параметра в -й выборке; ‑ среднее значение контролируемого параметра в -й выборке.

Шаг 10. Рассчитать значения следующих индексов:

• возможности технологического процесса по формуле (1);

• пригодности техпроцесса удовлетворять технический допуск без учета положения среднего значения (для процессов, стабильность которых по разбросу не подтверждена) по формуле

; (4)

• пригодности техпроцесса удовлетворять технический допуск с учетом положения среднего значения (для процессов, стабильность которых по разбросу не подтверждена) по формуле

или . (5)

Аналогично, при высоких значениях или, если задано одно из предельных значений, то рассчитать критический индекс пригодности процесса

или .

Шаг 11. Оценить потенциальные возможности процесса по показателю , а также фактические возможности процесса по индексам и .

Если значения процесс непригоден для установленных требований. Необходимо принять меры, направленные на обеспечение стабильности среднего; если процесс оставить без улучшений, то уровень несоответствий будет непрогнозируемым. Оптимальным значением считается .

Шаг 12. Найти полную изменчивость процесса по формуле (3)

Шаг 13. Рассчитать значения индексов:

• пригодности техпроцесса удовлетворять технический допуск без учета положения среднего значения по формуле (4);

• пригодности техпроцесса удовлетворять технический допуск с учетом положения среднего значения по формуле (5).

Шаг 14. Оценить возможности технологического процесса по индексам и . Принять меры, направленные на обеспечение стабильности размахов.

Пример. Станок производит электронные диски с заданной толщиной от 0,007 до 0,0162 мм. Оценить возможности технологического процесса, если карта медиан и карта размахов показали, что процесс находится в состоянии статистической управляемости (рис. 3).

Так как процесс стабилен, то проведем оценку собственной изменчивости процесса по формуле

,

где с учетом того, что равно 2,326

Найдем показатели возможности процесса по индексам:

• возможности технологического процесса по формуле

, (1)

• воспроизводимости процесса по формуле

1 В качестве независимых условий («связей»), наложенных на частоты , могут выступать: условие (1), требование о совпадении статистического среднего с гипотетическим, условие о совпадении дисперсий и т.п.

89