
Razdel4
.docР |
60 |
70 |
80 |
90 |
95 |
97 |
99 |
99,73 |
z |
0,84 |
1,03 |
1,29 |
1,65 |
1,96 |
2,18 |
2,58 |
3,0 |
Пример. Для получения необходимой плотности намотки осуществляется натяжение провода. Изменение усилия натяжения провода при наматывании приводит к изменению сопротивления. Во время операции намотки катушки контура контролируемый параметр сопротивления имеет номинальное значение 75 Ом со среднеквадратичным отклонением 2,62 Ом. Сколько операций намотки нужно проконтролировать для оценки среднего сопротивления с точностью в 3%.
Найдем допустимую абсолютную ошибку
![]() Ом
Ом
По таблице находим значение квантиля распределения, соответствующего доверительному интервалу 97% (ошибке в 3%). Оно равно 2,18, а значит объем выборки операций равен:
![]() .
.
Таким образом, необходимо проконтролировать 5 случайно выбранных операций.
Кривая нормального распределения характеризует величину случайных ошибок:
- ошибка, постоянная в пределах партии, на форму кривой распределения не влияет – она вызывает сдвижку всей кривой по оси абсцисс;
- закономерно изменяющиеся ошибки влияют на форму кривой распределения.
На рис. 1 показана
полученная кривая плотности нормального
распределения, расположенная в пределах
поля допуска, ограниченного нижним
предельным значением
![]() и верхним предельным значением UCL.
Площадь под кривой между двумя предельными
значениями представляет собой ту долю
совокупности, для которой значения
лежат в пределах поля допуска, т.е. долю
годной продукции
и верхним предельным значением UCL.
Площадь под кривой между двумя предельными
значениями представляет собой ту долю
совокупности, для которой значения
лежат в пределах поля допуска, т.е. долю
годной продукции
![]() .
Эта доля определяется как вероятность
того, что случайная величина примет
значение в пределах от
до UCL,
т.е.
.
Эта доля определяется как вероятность
того, что случайная величина примет
значение в пределах от
до UCL,
т.е.
![]() .
.
Примечание |
Значения
|
Из этой формулы
следует, что доля годной продукции
зависит от допуска, а также от значений
и
![]() .
Чем больше будет поле допуска, тем
большей будет доля годной продукции, и
наоборот, чем большим будет значение
,
тем меньшей будет доля годной продукции
и тем больше будет доля дефектной
продукции
.
.
Чем больше будет поле допуска, тем
большей будет доля годной продукции, и
наоборот, чем большим будет значение
,
тем меньшей будет доля годной продукции
и тем больше будет доля дефектной
продукции
.
Сказанное можно проиллюстрировать графиками на рис. 1, сравнивая площади под нормальными кривыми в пределах поля допуска при различных значениях : 0.5; 1; 2.

Рис. 1. Влияние параметров кривой плотности нормального распределения
на долю годных и дефектных изделий
С другой стороны, чем больше будет отклоняться от номинального значения (при неизменном ), тем меньшей будет доля годной продукции и тем большей будет доля дефектной продукции (рис. 2).
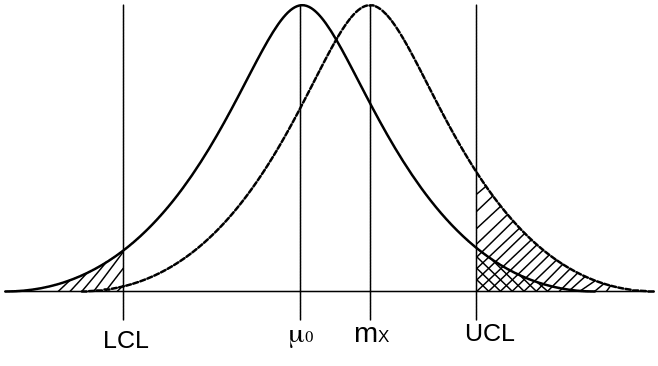
Рис. 2. Изменение доли дефектной продукции при
разладке технологического процесса
Пример.
Предположим, что технологический процесс
налажен; известно, что
![]() ,
,
![]() .
Кроме того, в соответствии с требованиями
нормативно-технической документации
установлен следующий допуск на изделие
.
Кроме того, в соответствии с требованиями
нормативно-технической документации
установлен следующий допуск на изделие
![]() .
Найти долю изделий, отвечающий
установленным требованиям, и долю
дефектной продукции.
.
Найти долю изделий, отвечающий
установленным требованиям, и долю
дефектной продукции.
Долю годных изделий
определим через вероятность того, что
случайная величина примет значение в
пределах от
![]() до
до
![]() ,
т.е.
,
т.е.
![]() .
.
Соответственно,
доля дефектных изделий составит
![]() .
.
Основная цель предварительного анализа состояния технологического процесса состоит в том, чтобы на основе полученных результатов, в случае необходимости, привести процесс в статистически управляемое состояние.
Использование метода кривых распределения позволяет:
- оценить физическую точность технологического процесса;
- оценить соответствие технологического процесса заданным допускам;
- определить процент вероятного брака;
- сравнивать разные процессы по их точности;
- определять степень стабильность технологических процессов;
- исследовать влияние отдельных факторов.
Несмотря на простоту, надежность и универсальность, метод кривых распределения не учитывает последовательность обработки деталей. Все детали как бы перемешиваются. Переменные систематические ошибки не отделяются от случайных, а их влияние проявляется в виде рассеивания размеров.
Для устранения этих недостатков используются точностные диаграммы, на которых указывают положение центра группирования, среднее квадратическое отклонение, поле рассеивания в разные моменты времени.
Точностная диаграмма, определяющая суммарный закон распределения ошибок в партии изделий, может быть получена:
статистически по результатам измерения выборки в ходе технологического процесса;
расчетным путем по результатам теоретических исследований с учетом нормативных данных.
Алгоритм построения статистических точностных диаграмм следующий.
Шаг 1. Составляется
генеральная совокупность результатов
наблюдения за параметрами, находятся
основные статистические характеристики
выборки (
,
![]() ).
).
Ш
Рис. 3. Точностная
диаграмма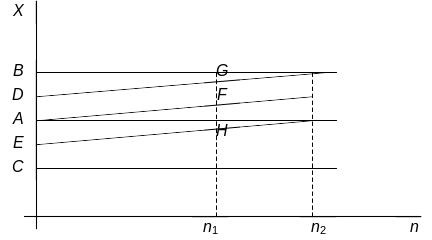
на оси y отложить номинальное значение контролируемого параметра и обозначить границы поля допуска (точки А, В, С на рис. 5.3);
через точки А, В, С провести прямые, параллельные оси х;
предполагая, что в начальный момент
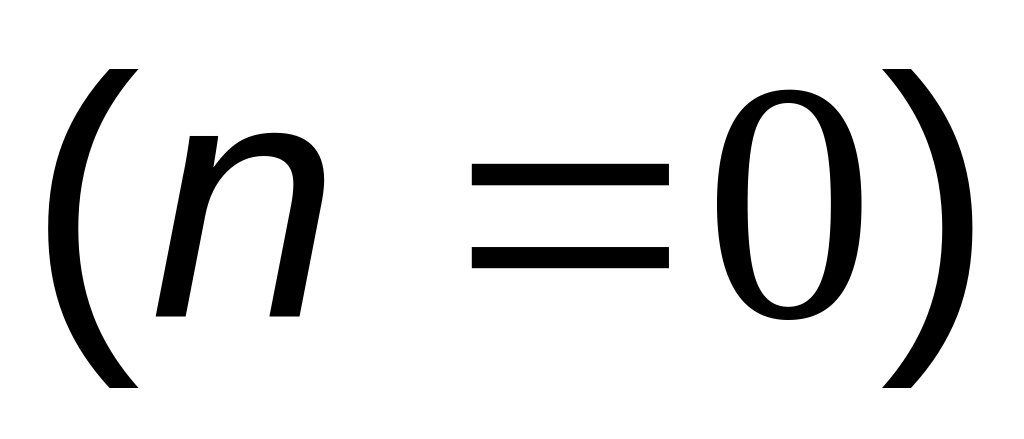 математическое ожидание контролируемого
параметра X
совпадает с его номинальным значением,
а
определено, отложить на оси y
значения
математическое ожидание контролируемого
параметра X
совпадает с его номинальным значением,
а
определено, отложить на оси y
значения
 ,
,
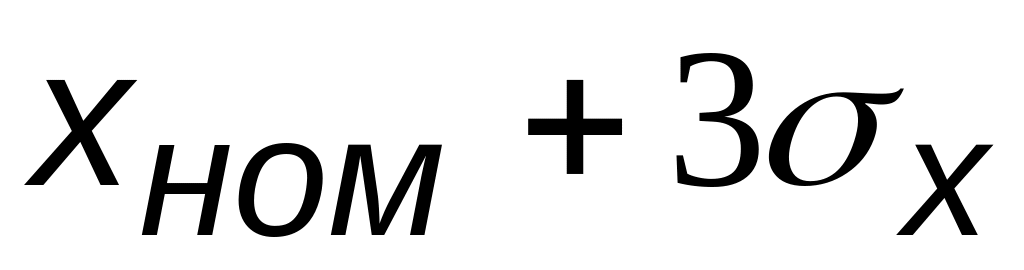 и
и
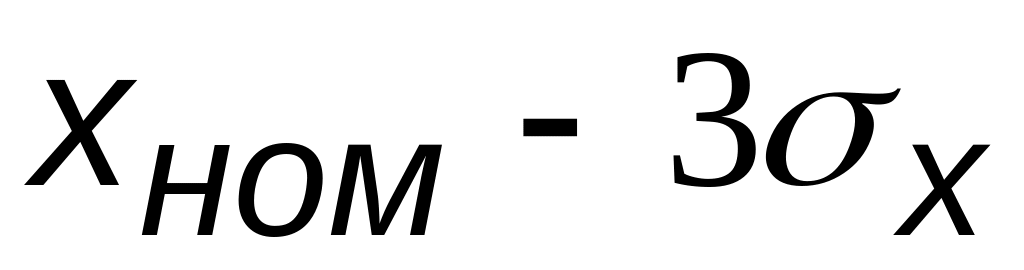 (соответственно точки А, D,
E на рис. 3);
(соответственно точки А, D,
E на рис. 3);обозначить на оси х значение n1, соответствующее объему выборки, через нее провести прямую, параллельную оси y; на этой прямой отложить значения ,
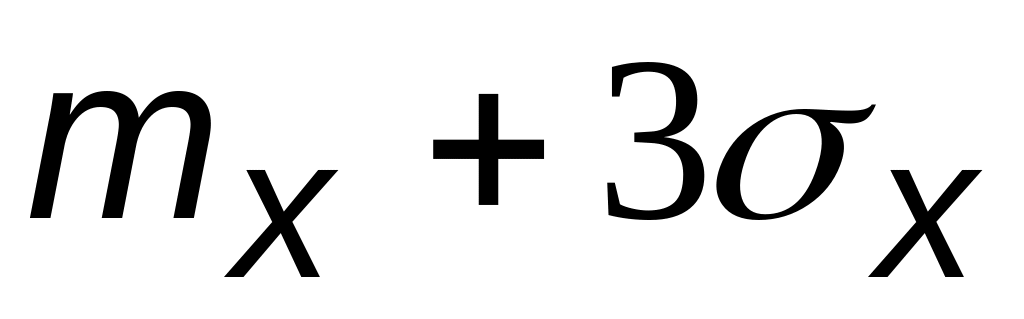 и
и
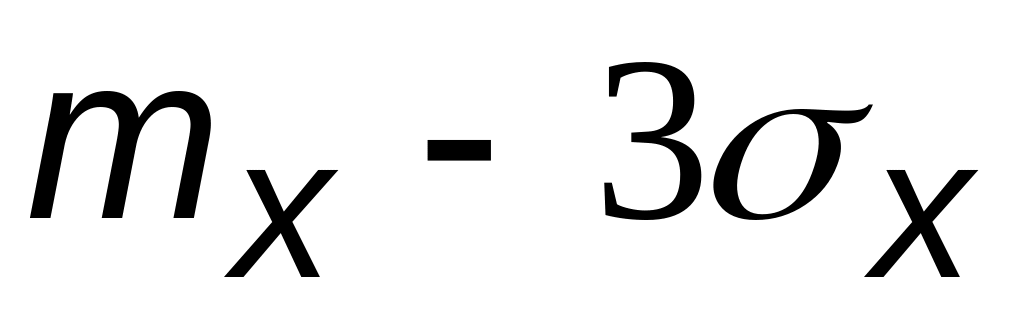 (соответственно точки F,
G,
H
на рис. 3), полученные при обработке
статистического материала;
(соответственно точки F,
G,
H
на рис. 3), полученные при обработке
статистического материала;провести прямые АF, DG, EH; моменты пересечения границ поля допуска с этими прямыми определяют момент подналадки оборудования (точка n2 на рис. 3).
По точностной диаграмме определяется не менее важная характеристика технологического процесса - стабильность, заключающаяся в способности сохранять значения и σ неизменными в течение некоторого времени.
Как уже отмечалось, изменение положения центра группирования характеризует воздействие систематических факторов на точность, а рассеивание в каждый момент – «мгновенное» рассеивание, обусловленное случайными факторами.
Расчет точности технологических процессов во времени. Здесь основой служит метод контрольных карт (карт Шухарта – ГОСТ 50779.42-99) – графический метод оценки степени статистически неуправляемого состояния процесса путем сравнения значений отдельных статистических данных из серии выборок (подгрупп) с контрольными границами. Предположения, касающиеся сбора данных, точной формы их распределения, отсутствие или невозможность экономического анализа неслучайных (необнаруженных) причин, исключили возможность использования строгого теоретико-вероятностного метода.
Наименование изделия |
Показатель качества |
Единица измерения |
№ стандарта |
|||||||||
Дневная норма |
Операция |
№ станка |
Объем выборки |
|||||||||
Оператор |
Контролер |
Разработчик к/к |
||||||||||
Нормативы UTL LTL |
Дата |
Отдел |
||||||||||
Срок изготовления с по |
Период сбора данных с по |
Стоимость детали |
||||||||||
№ подгруппы |
1 |
2 |
3 |
4 |
5 |
… |
25 |
|||||
Значе-ния измере-ний |
1 |
|
|
|
|
… |
|
|||||
2 |
|
|
|
|
… |
|
||||||
… |
… |
… |
… |
… |
… |
… |
||||||
10 |
|
|
|
|
|
|
||||||
Средние |
|
|
|
|
|
|
|
|||||
Размахи |
|
|
|
|
|
|
|
|||||
Среднее
|
|
|
|
|
|
|
|
|||||
Размах
|
|
|
|
|
|
|
|
|||||
Рис. 1. Форма для получения контрольной карты
Статистическая оценка точности технологических процессов заключается в том, что в определенные моменты времени из совокупности единиц продукции, прошедших технологический процесс, отбирают выборку и измеряют контролируемый параметр (рис. 1). По результатам измерений определяют статистические характеристики, значения которых наносят на контрольную карту, и в зависимости о положении точек относительно границ в соответствии с ГОСТ 50779.42 – 99 судят о налаженности или разлаженности технологического процесса.
При анализе точности и стабильности технологических операций предполагают, что процесс находится в статистически управляемом состоянии, а значит можно предсказывать его ход до тех пор, пока неслучайные (особые) причины не станут воздействовать на него, в результате чего процесс выводится из статистически управляемого состояния. В последнем случае результат не может быть предсказан при отсутствии информации об этих воздействиях. Такой статистически неуправляемый процесс нуждается в определенном вмешательстве для приведения его в статистически управляемое состояние. Если способы вмешательства в процесс по некоторым экономическим или другим причинам отсутствуют, то по контрольным картам определяют только факт статистически неуправляемого состояния.
Контрольные границы (границы регулирования) используют в качестве критерия для сигнализации о необходимости управления технологическим процессом, которое может иметь следующие формы:
- определение причины статистически неуправляемого состояния;
- регулирование процесса;
- остановки процесса.
Контрольные границы – средство определения статистически управляемого состояния технологического процесса. Правила, по которым определяют причины превышения контрольных границ (границ регулирования) или предупреждающих границ, установлены специальными международными стандартами на контрольные карты (ISO 7966, ISO 8258, ГОСТ Р 50779.41-96). Процесс считают разлаженным, если:
Некоторые точки выходят за контрольные пределы.
Серия из семи точек оказалась по одну сторону от средней линии.
Четырнадцать попеременно возрастающих и убывающих точек.
Имеется тренд (точки образуют непрерывно повышающуюся или непрерывно понижающуюся кривую).
Две – три точки оказываются за предупредительными двухсигмовыми границами.
Если большинство точек находится внутри полутарасигмовых линий, что означает, что в подгруппах смешиваются данные из различных распределений.
Контрольные границы шире поля допуска (в идеале контрольные границы должны составлять
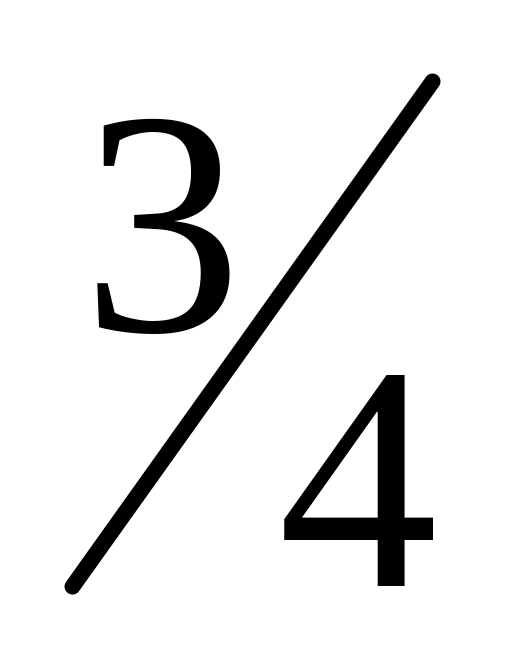 величины поля допуска).
величины поля допуска).Восемь последовательных точек по обе стороны от центральной линии и ни одной в односигмовой зоне.
Если контрольная карта показывает, что процесс разлажен, находят причины разладки и производят наладку. Систематическое устранение особых причин избыточной изменчивости приводит технологический процесс в состояние статистической управляемости, а, значит, точность производства предсказуема, процесс пригоден для удовлетворения требований, установленных в нормативных документах.
Если процесс налажен (достигнута необходимая точность и стабильность) на контрольную карту продолжают наносить точки, но через 20…30 точек пересчитывают контрольные границы.
Рассмотрим карты по количественным признакам. Для статистического регулирования технологических процессов, как правило, используют две карты:
карты для регулирования уровня настройки (стабильности) технологических операций по найденной мере расположения (центру) количественных данных (карта средних арифметических (
 -карта),
карта медиан (
-карта),
карта медиан (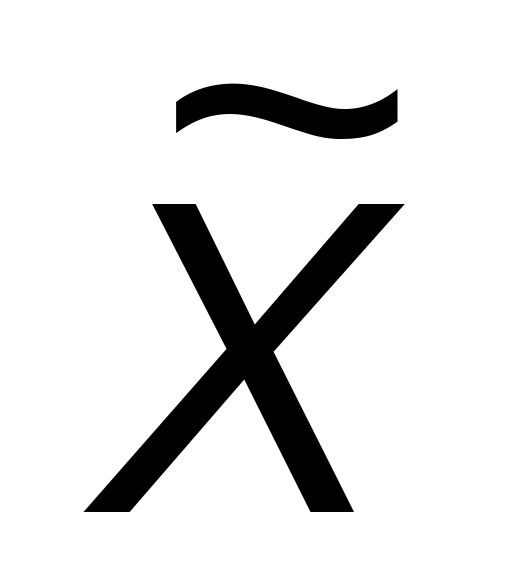 -карта));
-карта));карты для регулирования точности технологических операций, по найденной мере разброса (рассеивания) (карта средних квадратичных отклонений (
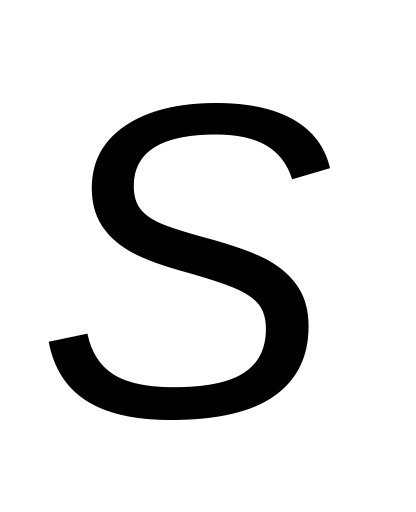 -карта),
карта размахов (
-карта),
карта размахов (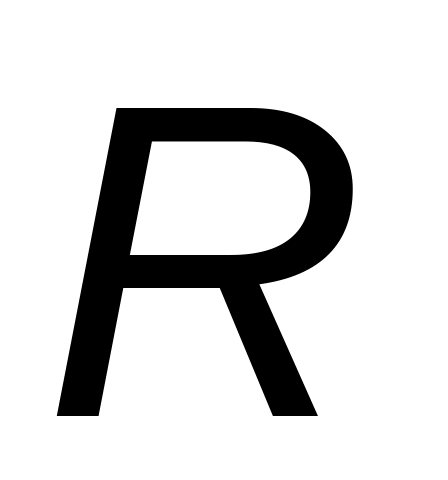 -карта),
карта индивидуальных значений (
-карта)).
-карта),
карта индивидуальных значений (
-карта)).
Пример |
Карты расположения применяют в случаях, когда необходимо оценить, произошел ли сдвиг в уровне процесса, карты разброса - чтобы определить наличие изменения значения стандартного отклонения в выборках или подгруппах. |
Одновременное
введение двух карт называется методом
статистического регулирования,
например, метод
![]() средних арифметических значений и
размахов, используемый для технологических
процессов с высокими требованиям
точности, лабораторных экспресс –
анализов и т.д.
средних арифметических значений и
размахов, используемый для технологических
процессов с высокими требованиям
точности, лабораторных экспресс –
анализов и т.д.
Существует два типа контрольных карт.
1. Карты, на которых контрольные границы определены установленными стандартными значениями. Стандартные значения устанавливают с учетом таких факторов:
экономических соображений, потребностей в изделии и затрат на производстве;
желательного или требуемого (установленного) значения, указанного в технической документации;
представительных предварительных данных, полученных на практике с помощью контрольных карт при отсутствии указанных стандартных величин.
Контрольные карты этого типа применяют:
для определения, будут ли выборочные значения отличаться от установленных стандартных значений;
для оценки соответствия системы причин, влияющих на процесс, указанным в технической документации.
В качестве примера рассмотрим карты средних значений и среднеквадратических отклонений, используемых для контроля отклонения параметра от нормы (для настройки на норму) и для контроля рассеяния показателя технологического процесса соответственно.
Предположим, что
стандартное отклонение исходных
одиночных измерений
![]() известно, что справедливо, когда полностью
известна точность используемого в
технологическом процессе оборудования,
а также точность параметров материалов
и комплектующих. Пусть также задан
известный из технических условий центр
настройки технологического процесса
известно, что справедливо, когда полностью
известна точность используемого в
технологическом процессе оборудования,
а также точность параметров материалов
и комплектующих. Пусть также задан
известный из технических условий центр
настройки технологического процесса
![]() .
В этом случае центральная линия берется
равной
.
В этом случае центральная линия берется
равной
![]() ,
а верхняя и нижняя границы определяются
по формулам
,
а верхняя и нижняя границы определяются
по формулам
![]() и
и
![]() ,
,
где
![]() ,
- верхняя и нижняя границы значений
измеряемого параметра соответственно
(обозначение по ГОСТ 50779.42 – 99);
- объем выборки.
,
- верхняя и нижняя границы значений
измеряемого параметра соответственно
(обозначение по ГОСТ 50779.42 – 99);
- объем выборки.
Точки на контрольной карте – это средние значения небольших выборок (подгрупп) одинакового объема обычно в 3 …10 элементов, которые определяются по формуле:
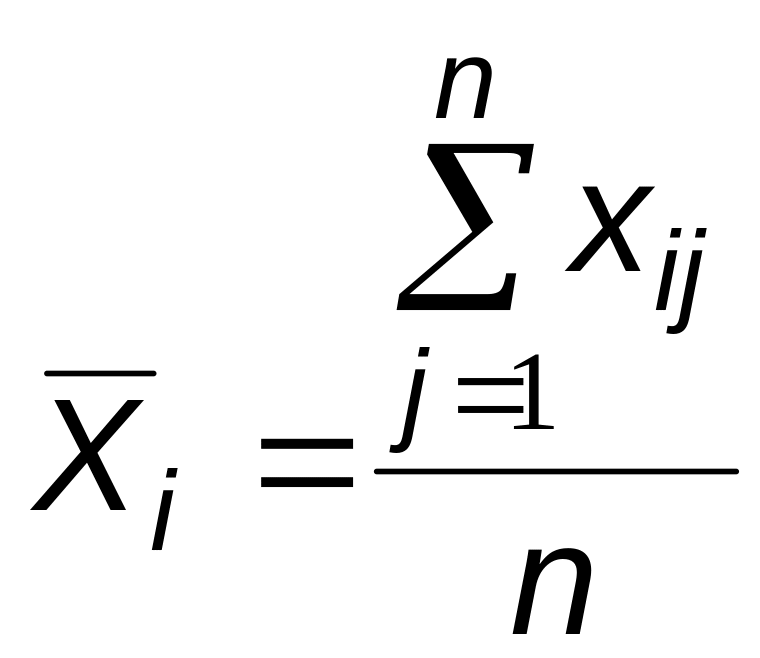 , (1)
, (1)
где
![]() ‑ возможное значение контролируемого
параметра в
‑ возможное значение контролируемого
параметра в
![]() -й
выборке.
-й
выборке.
Пример. Менеджер по качеству импорта чая на основании подобных процессов предъявляет требования к процессу упаковки такие, чтобы средний вес упаковки был 100,6 г. И предполагаемое стандартное отклонение процесса 1.4 г – получено на основе аналогичных упаковочных процессов.
Для контроля было взято 10 выборок объема 5. Значения средних представлены в таблице.
k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
100,6 |
101,3 |
99,6 |
100,5 |
99,9 |
99,5 |
100,4 |
100,5 |
101,1 |
100,3 |
Отклоняется ли технологический процесс упаковки чая от аналогичных упаковочных процессов?
Так как стандартные значения упаковочного процесса заданы, то
![]() ,
,
![]() ,
,
![]() .
.
Контрольная карта представлена на рис. 2, анализ которой показывает, что технологический процесс не соответствует аналогичным процессам упаковки. Он стабилен.
Т
Рис. 2 Контрольная карта к примеру
Средние квадратичные отклонения для каждой выборки определяем по формуле
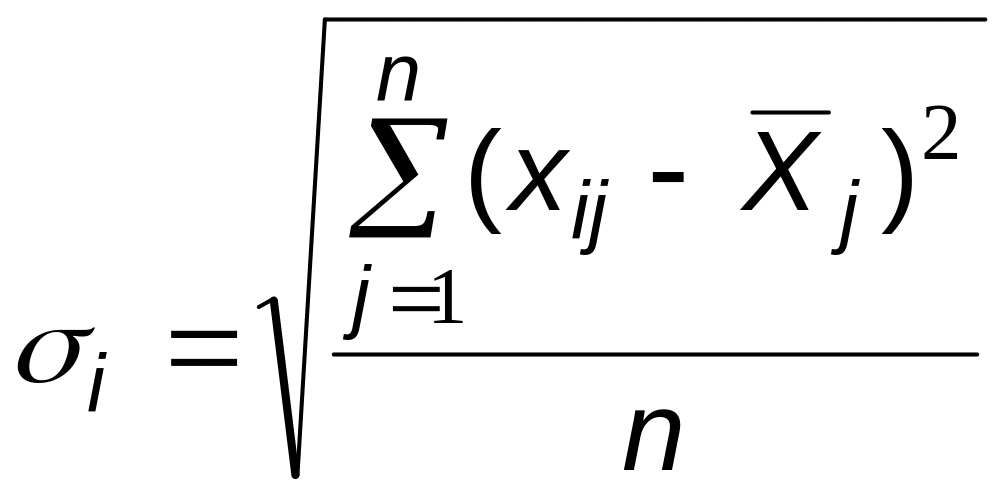 , (2)
, (2)
Средняя линия -карты - это среднее из средних квадратичных значений выборок, т.е.
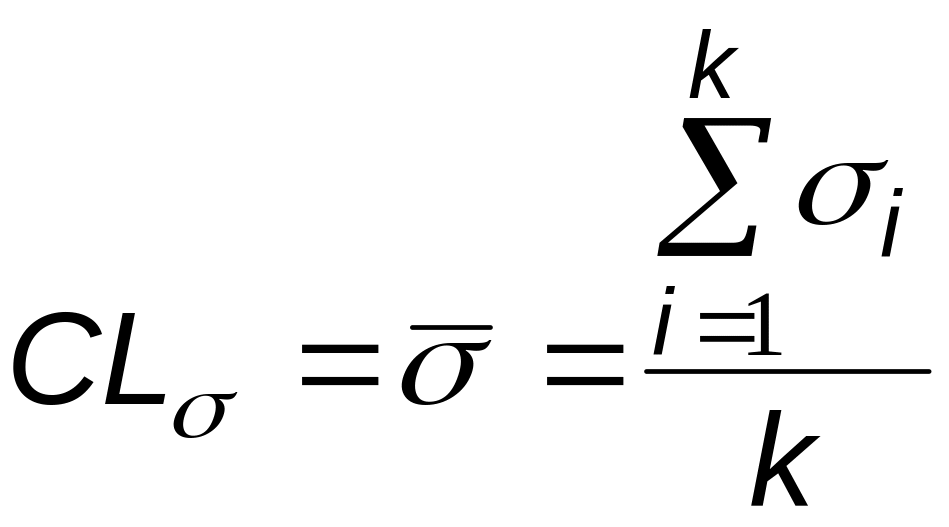 , (3)
, (3)
где
![]() - среднеквадратичное отклонение
контролируемого параметра в
-й
выборке, (
- среднеквадратичное отклонение
контролируемого параметра в
-й
выборке, (![]() ).
).
Контрольные границы в случае, если стандартные значения процесса известны, определяют по формулам:
![]() и
и
![]() ,
,
где - известное стандартное отклонение технологического процесса, а коэффициенты определены таблицей
n |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
0,000 |
0,000 |
0,000 |
0,000 |
0,029 |
0,113 |
0,179 |
0,232 |
0,276 |
|
2,606 |
2,276 |
2,088 |
1,964 |
1,874 |
1,806 |
1,751 |
1,707 |
1,669 |
2. Карты, на которых контрольные границы рассчитаны на основе выборочных данных, что справедливо в случае, когда технические условия процесса не определены. В этом случае расчет параметров контрольной карты производится по следующим формулам (на примере карты средних арифметических ( -карта) и карты медиан ( -карта)).
Для -карты находят среднее значение выборок, определяющее среднюю линию по формуле
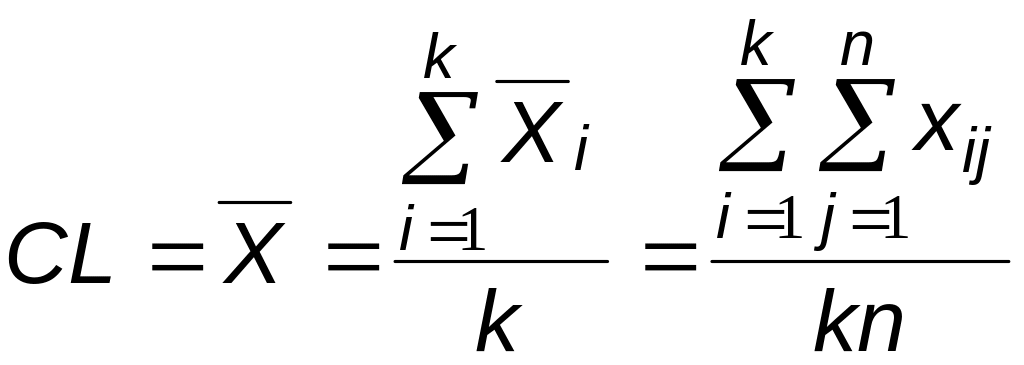 , (4)
, (4)
где
![]() ‑ среднее значение контролируемого
параметра в
-й
выборке (
‑ среднее значение контролируемого
параметра в
-й
выборке (![]() );
);
![]() ‑ число подгрупп (число точек).
‑ число подгрупп (число точек).
