
Razdel4
.doc
ОСНОВНЫЕ МЕТОДЫ РАСЧЕТА ТОЧНОСТИ ПРОИЗВОДСТВА РЭА
Основные вопросы:
Основы статистического анализа точности производства.
Оценка точности производства с помощью кривых распределения и точностных диаграмм.
Расчет точности производства РЭА во времени.
Показатели возможностей технологических процессов.
Основы статистического анализа точности производства. Под точностью производства понимают степень соответствия изготовленного изделия заданным формам, размерам, механическим и физическим свойствам, определяемым назначением этого изделия и т.д. Точность производства - один из основных критериев его качества и надежности.
Обеспечение точности - комплексная проблема. Ее успешное решение возможно при едином рассмотрении задач продуктивности, экономичности и качества производства. Решение этой проблемы проводят на всех этапах создания изделия: при разработке принципиальных схем и конструкторской документации, во время проектирования и выполнения технологических процессов, при измерениях и контроле.
Отклонения технологического процесса от расчетного являются причинами производственных ошибок. Производственные ошибки делят на категории:
Систематические:
– постоянные;
– повторяющиеся без изменения при изготовлении каждой детали;
2. Переменные:
– изменяющиеся от детали к детали по определенному закону;
– случайные, изменяющиеся от детали к детали случайным образом.
Производственные ошибки относят к группам первичных ошибок, которые по своей природе достаточно разнообразны, но их классификация имеет большое значение при выборе аналитического метода расчета точности и метода расчета суммарной ошибки.
В общем случае первичные ошибки делят на четыре группы:
теоретические;
ошибки настройки;
ошибки установки;
ошибки обработки.
Теоретические ошибки возникают вследствие сознательного использования вместо точной приближенной схемы обработки (например, в случае упрощения технологического процесса при обеспечении заданной точности) или при использовании инструмента с приближенным профилем.
Ошибки настройки технологического оборудования связаны с ошибками неточных приборов, используемых при его настройке, с ошибками настройщика и т.п. ошибками, не позволяющими провести наладку оборудования с абсолютной точностью. Эти ошибки существенно влияют на точность обработки, что особенно заметно в условиях приборостроительного производства, где величина суммарной ошибки существенно зависит от величины ошибки настройки.
Ошибки установки у определяются суммарным значением:
ошибки базирования, б, возникающие в случае, когда технологическая база не совпадает с конструкторской;
ошибки закрепления з, связанные с деформацией поверхностных слоев базовых поверхностей детали при закреплении, а также с отклонением поверхности базовой детали при закреплении.
На точность обработки существеннее влияет ошибка базирования, а ошибкой закрепления можно пренебречь, т.е. фактически
у=б.
При выборе метода расчета точности ошибки обработки условно делят на две группы:
Ошибки, не зависящие от нагрузки – неточность оборудования и неточность инструмента и приспособлений;
Ошибки, зависящие от нагрузки:
пружинные деформации технологической системы «станок – приспособление – инструмент – деталь»;
температурные деформации технологической системы;
размерный износ режущего инструмента;
внутренние напряжения обрабатываемой детали.
К первой группе ошибок относят ошибки измерения. Они могут достигать существенного значения в суммарной ошибке в зависимости от выбранных средств измерения.
Пример |
При измерении внешнего диаметра вала получаются такие ошибки: 0,001 мм при измерении оптиметром; 0,01 мм при измерении микрометром; 0,1 …0,15 мм при использовании штангенциркуля. |
Поэтому при расчете точности обработки обязательно необходимо учитывать ошибки измерений, учитывая, что они приводят к уменьшению допуска на остальные составляющие суммарной ошибки.
При расчете точности производства метод расчета зависит от характера ошибок:
– в условиях обработки одной партии их принимают постоянными систематическими;
– для обработки совокупности партий их принимают случайными.
Точность технологических процессов можно определить двумя методами:
Теоретическим, т.е. предварительным, проведенным заранее и осуществленном в виде:
расчетно-аналитического метода;
вероятностного метода.
Экспериментальным, проведенным после того, как процесс свершился в производственных условиях.
Расчетно-аналитический метод требует полной детерминированности процесса. Тут решают систему уравнений, описывающих закономерности ошибок технологического процесса, однозначно определяют требуемую точность. Для детерминированного процесса при том же самом комплексе входных условий при каждом последующем расчете получают один и тот же результат.
Однако реальные процессы не могут быть описаны детерминированными моделями, и правильность использования этих моделей зависит от степени изученности производственного процесса. Математическое описание процессов в этом случае состоит в последовательном определении начальных ошибок, далее в аналитическом виде определяют их влияние на конечную точность готовой детали, и решают полученную систему уравнений. Во время реализации такого метода возникают следующие трудности:
невозможность учета всех факторов, влияющих на точность технологического процесса;
расчет требует составления и решения большого количества взаимосвязанных уравнений;
по точности изготовления одного изделия невозможно сделать выводы о точности технологического процесса в целом.
Этот метод используют для оценки воздействия некоторых факторов в определенных условиях производства, но для комплексной оценки точности он не годится.
Вероятностный метод используют для анализа точности контролируемых параметров в партии деталей, а также для оценки точности процесса в целом, т.е. охватывая практически все возможные и важные комбинации условий протекания технологического процесса.
Вероятностная модель может содержать:
- законы распределения контролируемых параметров;
- характеристики систематического изменения контролируемых параметров;
- характеристики рассеивания контролируемых параметров, как для отдельных партий, так и для процесса в целом.
При построении вероятностной модели справедливо следующее правило:
при определенных условиях случайные величины начинают вести себя практически как неслучайные, что позволяет уверенно оперировать с ними и предсказывать результаты массовых случайных явлений почти с полной определенностью. |
Это правило справедливо при условии, что влияние на сумму отдельных слагаемых должно быть равномерно малым.
При выполнении этого правила рассмотрим следующие утверждения.
Утверждение 1. При достаточно большом количестве независимых опытов среднее арифметическое наблюдаемых значений случайной величины сходится по вероятности к ее математическому ожиданию.
Утверждение 2. Если исследуемая случайная величина может быть представлена в виде суммы большого числа независимых (или слабо зависимых) элементарных слагаемых, каждое из которых отдельно сравнительно мало влияет на сумму, то закон распределения суммы становится приблизительно нормальным. Это правило называется центральной предельной теоремой.
Следствие из
утверждения 2.
Пусть
![]() – независимые случайные величины с
математическими ожиданиями
– независимые случайные величины с
математическими ожиданиями
![]() и дисперсиями
и дисперсиями
![]() .
Предположим, что условия центральной
предельной теоремы выполняются, т.е.
число слагаемых
.
Предположим, что условия центральной
предельной теоремы выполняются, т.е.
число слагаемых
![]() достаточно для того, чтобы закон
распределения величины
достаточно для того, чтобы закон
распределения величины
![]()
можно считать приблизительно нормальным.
Тогда вероятность
того, что случайная величина
![]() попадает в границы участка
попадает в границы участка
![]() ,
выражается формулой
,
выражается формулой
![]() ,
,
где
![]() ,
,
![]() – математическое ожидание и
среднеквадратическое отклонение
величины
,
– математическое ожидание и
среднеквадратическое отклонение
величины
,
![]() - нормальная функция распределения
(табличная функция).
- нормальная функция распределения
(табличная функция).
Отметим, что функция
![]() имеет такие свойства:
имеет такие свойства:
![]() ;
;
![]() ;
– неубывающая функция.
;
– неубывающая функция.
Кроме того, из
симметричности нормального распределения
с параметрами
![]() ,
,
![]() относительно начала координат следует,
что
относительно начала координат следует,
что
![]() .
.
Пример. Браковка
шариков для подшипников проводится
таким образом: если шарик не проходит
через отверстие диаметром
![]() ,
но проходит через отверстие диаметром
,
но проходит через отверстие диаметром
![]() ,
то его размер считается приемлемым.
Если какое-нибудь из этих условий не
выполняется, то шарик бракуется. Известно,
что диаметр шарика
,
то его размер считается приемлемым.
Если какое-нибудь из этих условий не
выполняется, то шарик бракуется. Известно,
что диаметр шарика
![]() – нормально распределенная случайная
величина с характеристиками
– нормально распределенная случайная
величина с характеристиками
![]() и
и
![]() .
Найти вероятность того, что шарик будет
забракован.
.
Найти вероятность того, что шарик будет
забракован.
Вероятность браковки шарика равняется
![]() ,
,
где Р
– вероятность того, что шарик не будет
забракован, которую из условий отбраковки
определим как
![]() .
Отсюда запишем
.
Отсюда запишем
![]() .
.
Учитывая значение
![]() ,
найдем
,
найдем
![]()
Из условия получим
![]() .
.
Учитывая значения
![]() ,
по таблицам функции Лапласа найдем
,
по таблицам функции Лапласа найдем
![]() .
.
Реализация вероятностных методов связана со следующими трудностями:
сбор массовой технологической информации в производственных условиях достаточно сложный и трудоемкий процесс, хотя ее обработка на ЭВМ занимает несколько минут;
уменьшение объема информации нежелательно, так как это приводит к уменьшению надежности полученных результатов.
Пример |
В перспективных условиях данный метод может стать математической основой для систем автоматического мониторинга технологических процессов, когда соответствующие датчики регистрируют и накапливают соответствующие данные и передают их в ЭВМ в форме, удобной для восприятия. |
Тем не менее, при всех недостатках данного метода на практике широкое распространение получили следующие вероятностные методы:
оценка точности по кривым распределения;
оценка точности по точностным диаграммам;
оценка точности и стабильности по контрольным картам.
Оценка точности производства с помощью кривых распределения и точностных диаграмм. Для построения кривых распределения необходимо использовать экспериментальные данные о точности отдельных операций и отдельных параметров процесса. Эта информация может быть получена при измерении параметров технологического процесса при условии, что суммарная ошибка изготовления обусловлена рядом производственных недоминирующих ошибок. Характер рассеивания параметров деталей РЭА, определяющий точность технологических процессов, находят выборочным методом
Введем следующие определения.
Объем выборки - некоторое число объектов производства, отобранных из генеральной совокупности (партии) изделий. Эти объекты исследуют, по результатам проведенных исследований делают вывод о точности изготовления изделия (о его характерных свойствах) или о точности протекания производственного процесса.
Примечание |
Чем большее число единиц продукции будет проконтролировано, тем более точной будет оценка этих параметров. Продукцию на контроль следует отбирать при нормальном ходе производства, т.е. при надлежащем качестве сырья и при отлаженном оборудовании. |
Исходными данными
оценки точности производственных
процессов является совокупность из
наблюдений за контролируемым параметром,
в результате которых этот параметр
![]() принимает значения
принимает значения
![]() .
Такую совокупность называют простым
статистическим рядом. Соответственно
группированным (вариационным)
статистическим рядом называют
последовательность значений наблюдаемого
исследуемого параметра, расположенных
в порядке возрастания
.
Такую совокупность называют простым
статистическим рядом. Соответственно
группированным (вариационным)
статистическим рядом называют
последовательность значений наблюдаемого
исследуемого параметра, расположенных
в порядке возрастания
![]() .
.
Далее весь интервал изменения данных выборки (размах выборки) разбивают на разряды. Величиной разряда называют «удобное» число, ближайшего до числа, определенного по формуле
![]() ,
,
где
![]() - размах выборки;
- размах выборки;
![]() - число разрядов.
- число разрядов.
Статистической функцией распределения наблюдаемых параметров называют функцию, определенную равенством
![]()
где
![]() – границы разрядов в статистическом
ряде; i
– номер разряда в статистической
совокупности;
– границы разрядов в статистическом
ряде; i
– номер разряда в статистической
совокупности;
![]() – количество значений, приходящееся
на каждый разряд.
– количество значений, приходящееся
на каждый разряд.
Функцию
![]() называют полигоном накопленных частот,
изменяющимся в пределах от 0 до 1 и имеющим
скачки величиной
называют полигоном накопленных частот,
изменяющимся в пределах от 0 до 1 и имеющим
скачки величиной
![]() в точках
в точках
![]() (
(![]() ).
Все наблюдаемые параметры имеют
одинаковую вероятность
).
Все наблюдаемые параметры имеют
одинаковую вероятность
![]() .
.
При большом количестве наблюдаемых параметров статистическая совокупность становится громоздкой и неудобной для дальнейшей обработки. Поэтому для придания компактности строят практическую кривую распределения - гистограмму - по значениям группированной совокупности:
на оси абсцисс откладывают разряды и на каждом из них, рисуют прямоугольник, площадь которого равна частоте данного разряда:
![]() ,
при условии
,
при условии
![]() (1)
(1)
Полная площадь гистограммы равна 1.
На стадии предварительного анализа точности технологического процесса оценивают следующие параметры:
1. Математическое ожидание контролируемого параметра:
![]() ,
,
где
![]() ‑ возможное значение контролируемого
параметра;
‑ возможное значение контролируемого
параметра;
![]() ‑ вероятность появления значения
.
‑ вероятность появления значения
.
При большом количестве наблюдений для упрощения расчетов считают приближенно значение случайной величины в каждом разряде постоянным и равным среднему значению, которое выступает в роли «представителя» разряда. Тогда
![]() ,
,
где
![]() - «представитель» i
-го разряда;
- «представитель» i
-го разряда;
![]() - частота i
-го разряда; k
- число разрядов.
- частота i
-го разряда; k
- число разрядов.
2. Дисперсию случайной величины
![]()
или при большом количестве наблюдений -
![]() .
.
3. Среднее квадратическое отклонение
![]() .
.
Зная основные
статистические характеристики случайной
величины, можно найти вероятную долю
дефектной продукции
![]() при налаженном состоянии технологического
процесса.
при налаженном состоянии технологического
процесса.
При отклонении
![]() от заданного номинального значения
от заданного номинального значения
![]() ,
а также при увеличении
,
а также при увеличении
![]() увеличивается доля дефектной продукции
,
что свидетельствует о разладке
технологического процесса. Партия
деталей будет пригодной при выполнении
следующих условий:
увеличивается доля дефектной продукции
,
что свидетельствует о разладке
технологического процесса. Партия
деталей будет пригодной при выполнении
следующих условий:
математическое ожидание контролируемого параметра совпадает с серединой поля допуска
![]() . (2)
. (2)
Разница между
значениями
![]() и
и
![]() должна стремиться к нулю (в идеале
равняться нулю). В этом случае партия
деталей будет изготовлена без брака.
должна стремиться к нулю (в идеале
равняться нулю). В этом случае партия
деталей будет изготовлена без брака.
граничное практическое поле рассеивания равняется полю допуска
![]() . (3)
. (3)
Практическое граничное поле рассеивания параметров, подчиняющихся закону Гаусса, определяется соотношением
![]() .
.
Точность исследуемого технологического процесса сопоставляется с необходимой путем сравнения поля допуска с граничным практическим полем рассеивания р и определяется коэффициентом технологической точности
![]() .
.
Значение коэффициента
![]() соответствует удовлетворительной
организации технологического процесса:
этот процесс обеспечивает заданную
точность изготовления. При
соответствует удовлетворительной
организации технологического процесса:
этот процесс обеспечивает заданную
точность изготовления. При
![]() - технологический процесс требует
внимательных наблюдений, а при
- технологический процесс требует
внимательных наблюдений, а при
![]() часть изделий будет браком: необходимо
немедленно выяснять причину появления
дефектных изделий и принимать меры
управляющего воздействия.
часть изделий будет браком: необходимо
немедленно выяснять причину появления
дефектных изделий и принимать меры
управляющего воздействия.
Наиболее простое (качественное) представление о близости теоретического и эмпирического распределения дает графическое сравнение гистограмм с кривой распределения. Для количественной оценки соответствия эмпирического распределения с теоретическим используют ряд критериев, например, критерий Пирсона или Колмогорова.
В соответствии с
центральной предельной теоремой и в
предположении, что суммарная ошибка
изготовления обусловлена рядом
производственных недоминирующих ошибок,
закон распределения контролируемого
параметра предполагается приблизительно
нормальным (подчиненным закону Гаусса).
Алгоритм проверки закона распределения
по критерию Пирсона, показывающего меру
расхождения статистических вероятностей
![]() от гипотетических pi,
следующий:
от гипотетических pi,
следующий:
найти меру расхождения статистического распределения с гипотетическим по формуле
 ,
,
где k – число разрядов случайной величины; ni ‑ число значений в i–м разряде; pi ‑ гипотетическая вероятность, подчиненная теоретическому закону распределения;
учитывая полученное значение
 и число степеней свободы df
(число
разрядов минус число независимых
условий1),
наложенных на частоты
,
найти вероятность р
того, что величина, распределенная по
закону
и число степеней свободы df
(число
разрядов минус число независимых
условий1),
наложенных на частоты
,
найти вероятность р
того, что величина, распределенная по
закону
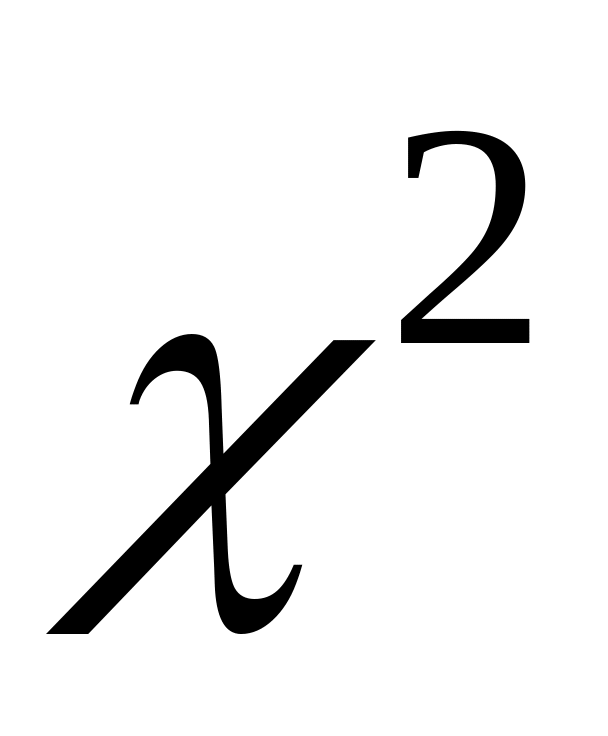 ,
превзойдет это значение.
,
превзойдет это значение.
Если вероятность р очень мала, это значит, что опытные данные противоречат гипотезе о теоретическом распределении значений x. Если вероятность р не мала, можно признать расхождения между теоретическим и гипотетическим распределениями несущественными и обусловленными случайными причинами. Гипотезу о выбранном теоретическом распределении значений x можно считать правдоподобной, если она не противоречит опытным данным. При этом значения р должны лежать в пределах 0.2 … 0.55.
Примечание |
Критерий равномерно реагирует на отличия распределений во всем диапазоне, но чувствителен к объему выборки и числу интервалов, на которые разбит диапазон переменной. |
Статистические исследования показали, что для большинства технологических процессов при отсутствии воздействия доминирующих факторов, существенно нарушающих ход операций, распределение подчиняется закону Гаусса. Даже в случае отклонения исследуемых экспериментальных данных от нормального закона существует, по крайней мере, два пути его целесообразной эксплуатации:
использовать нормальный закон в качестве первого приближения (при этом нередко оказывается, что подобное допущение дает достаточно точные с точки зрения конкретных целей исследования результаты);
провести преобразование исследуемой случайной величины, которое видоизменяет исходный "не нормальный" закон распределения в нормальный (например, провести большее число измерений контролируемого параметра и исходный биноминальный закон «превратиться» в нормальный; при уменьшении значений логнормальный закон «превращается» в нормальный и т.д.)
Существенных отступлений от этого закона можно ожидать в случае, когда среди действующих факторов есть один (несколько) доминирующих, подчиненных определенному (негауссовскому) закону.
Располагая некоторой информацией о характере вариации изучаемого признака, минимальный размер выборки при нормальном законе распределения с заданной точностью можно определить по формуле:
![]() ,
,
где
![]() – квантиль нормального распределения;
– квантиль нормального распределения;
![]() - задаваемая технологическими
требованиями абсолютная ошибка
распределения признака.
- задаваемая технологическими
требованиями абсолютная ошибка
распределения признака.
Примечание |
определяет степень точности технологического процесса, т.е. максимально допустимое значение между выборочным средним и номинальным значением контролируемого параметра. |
Значение отклонения
доверительного интервала
![]() от среднего значения в зависимости от
доверительной вероятности Р
результатов
от среднего значения в зависимости от
доверительной вероятности Р
результатов
