Допоміжна таблиця для пошуку розв’язку

	A	B	C	D	E	F	G
1	Оптимізація транспортних витрат
2	Постачаль-ники	Споживачі					Факт
3		1	1	1	1	1	5
4		1	1	1	1	1	5
5		1	1	1	1	1	5
6	Факт	3	3	3	3	3	15

Обчислюємо значення комірок у стовпці G від 3-го до 5-го рядків, кожне з яких є сумою значень у відповідних рядках від стовпця B по F, за допомогою вбудованої функції СУММ. Так, курсор вміщуємо до комірки G3, вибираємо послідовно Вставка функция, потім серед функцій вибираємо СУММ, і в комірці G3 з’являється вираз =СУММ(В3:F3). Після натискання Enter з’являється результат. Потім формулу розтягуємо на комірки G4 та G5.

Кожне значення у 6-му рядку „Факт” за стовпцями від В до F визначається як сума за кожним із стовпців з відповідною літерою від 3-го по 5-ий рядки. Наприклад, вантаж, який постачається споживачеві , тобто значення комірки В6 обчислюється за формулою =СУММ(В3:В5). Значення комірки G6 визначаємо як =СУММ(В6:F6) або як =СУММ(G3: G5), оскільки задача є закритою.

Далі на цьому ж робочому аркуші утворюємо ще одну таблицю, що містить інформацію про потреби, пропозицію та питому вартість перевезень між усіма учасниками транспортної задачі (табл. 6.2).

 Таблиця 6.2

Вихідна інформація

	A	B	C	D	E	F	G
7							Пропозиції
8		2	8	5	1	3	240
9		6	4	7	6	9	320
10		3	6	1	4	5	180
11	Потреби	100	120	160	210	150
12	Взагалом	11	18	13	11	17	70

У 12-му рядку за стовпцями В-F визначаємо загальну вартість перевезення вантажу, який одержує кожен із споживачів. Наприклад, для споживача (комірка В12) вартість перевезень можна визначити за формулою: =В3*В8+В4*В9+В5*В10. З цією ж метою можна також скористуватися функцією: СУММПРОИЗВ. Для цього значення комірки В16 визначаємо як =СУММПРОИЗВ(В3:В5; В8:В10). У комірці G12 за формулою  =СУММ(В12:F12) обчислюється загальна вартість перевезень. Отже, ця комірка містить значення цільової функції.

Для розв’язання транспортної задачі використовуємо процедуру Поиск решения (Сервис Поиск решения).

У полі Установить целевую ячейку даємо посилання на комірку з формулою загального вартості перевезень ($G$12), потім встановлюємо перемикач проти умови Равной: минимальному значению. До поля Изменяя ячейки вводимо посилання на комірки $В$3:$F$5 та додаємо обмеження на їх значення. Для цього ставимо курсор до вікна Ограничения, натискаємо кнопку Добавить, і на екрані з’являється діалогове вікно Добавление ограничения. До його лівого поля введемо ліву частину першого обмеження ($В$6:$F$6), вибираємо його знак в центральному полі (=) та до правого поля введемо правую частину обмеження ($В$11:$F$11). Отже, маємо: $В$6:$F$6=$В$11:$F$11. Це означає, що значення в комірках 6-го рядку повинні дорівнювати значенням у відповідних комірках 11-го рядку, тобто потреби споживачів необхідно повністю задовольнити. Слід зауважити, що надбудова Поиск решения дозволяє розв’язати й незбалансовану транспортну задачу без введення фіктивного учасника. У цьому випадку в центральному полі вікна Добавление ограничения вводять для споживачів знак >=, а для постачальників – знак <=. Тепер натискаємо Добавить і вводимо наступне обмеження: $G$3:$G$5=$G$8:$G$10, що означає, що всі запаси необхідно вивезти. Натискаємо кнопку ОК і повертаємося до діалогового вікна Поиск решения, яке набуває вигляду (рис. 6.1).

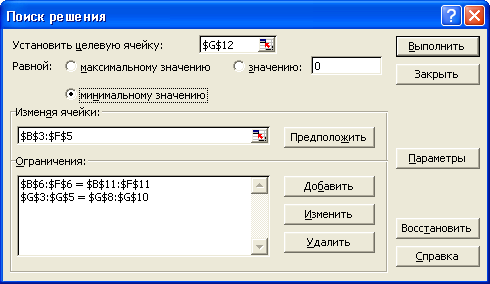
Рис. 6.1. Вигляд діалогового вікна Поиск решения після

введення обмежень транспортної задачі

Визначимо параметри моделі. Для цього натискаємо Парамеры і в діалоговому вікні Параметры поиска решения ставимо позначки до вічок Линейная модель та Неотрицательные значения, оскільки змінні транспортної задачі мають обмеження на знак. Натисканням кнопки OK повертаємося до діалогового вікна Поиск решения.

Отже, вся необхідна інформація введена. Для визначення оптимального плану транспортної задачі натискаємо кнопку Выполнить, внаслідок чого в табл. 6.1 та 6.2 змінюються: кількість вантажу (комірки В3:F5) та вартість перевезень (комірки В12:F12 та G12) приймають значення, що відповідають оптимальному плану. Одночасно з цим на екрані з’являється діалогове вікно Результаты поиска решения. Встановлюємо перемикач у положення Сохранить найденное решение й вказуємо Тип отчета: Устойчивость. Натискаємо ОК, і на робочому аркуші в таблиці, що відповідає табл. 6.1 – 6.2, зберігається розв’язок транспортної задачі (табл. 6.3), а звіт Устойчивость виводяться на окремий робочий аркуш (табл. 6.4).

Таблиця 6.3

Кінцевий вигляд розрахункової таблиці

	A	B	C	D	E	F	G
1	Оптимізація транспортних витрат
2	Постачаль-ники	Споживачі					Факт
3		0	0	0	110	130	240
4		100	120	0	100	0	320
5		0	0	160	0	20	180
6	Факт	100	120	160	210	150	740
7							Пропозиції
8		2	8	5	1	3	240
9		6	4	7	6	9	320
10		3	6	1	4	5	180
11	Потреби	100	120	160	210	150
12	Взагалом	600	480	160	710	490	2440

Розглянемо, яку інформацію містить кінцева таблиця.

Отже, завдяки застосуванню надбудови Поиск решения знайдено оптимальний план перевезень, який наведено у клітинах, які ми змінювали, тобто:

,

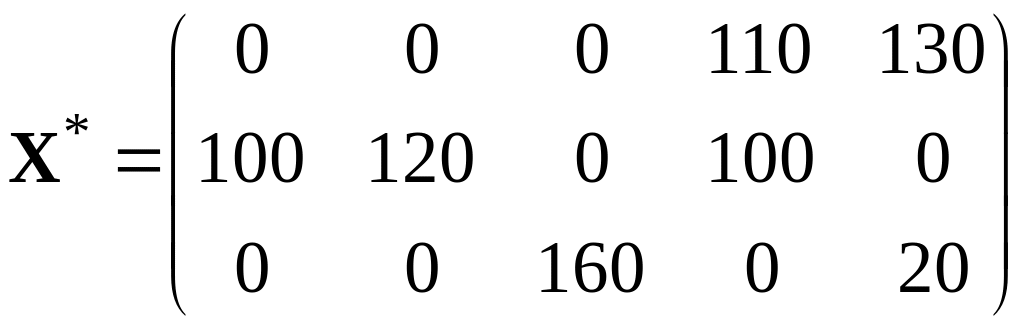за цим планом загальна вартість перевезень має мінімальне значення, яке дорівнює:

(ум. од.).

Перша з таблиць звіту Устойчивость містить вихідну інформацію, оптимальний план та деяку інформацію про можливі границі зміни коефіцієнтів цільової функції, в межах яких знайдений план лишається оптимальним, а також Нормированную стоимость, тобто оцінки оптимального плану транспортної задачі. Зверніть увагу, що комірка B5 за планом є вільною, однак їй відповідає нульова оцінка. Отже, задача має альтернативний оптимум.

Друга частина звіту містить відомості про тіньові ціни, тобто приховані потенціали учасників перевезення. Стовпчики Допустимое увеличение та Допустимое уменьшение містять інформацію про межі, в яких можна змінювати праву частину кожного з обмежень окремо, при цьому план задачі буде залишатися оптимальним. Оскільки коміркам C6 та D6 відповідають від’ємні потенціали, то збільшення потреб або споживача , або в межах припустимого призведе до зменшення цільової функції. Так, збільшимо потреби на 20 одиниць, а щоб задача лишилася закритою, збільшимо запаси на 20 одиниць. Результат наведено в табл. 6.5.

Таблиця 6.4